Контакты

Случайная статья

Актуализация имеющихся знаний (устная работа).

Стр 1 из 2Следующая ⇒

22 группа Гаврилина Л.А.

09.12.2020 года Математика

Изучение нового материала

Тема. Формулы удвоения

Сегодня на уроке мы выведем формулы тригонометрии – формулы двойного аргумента и рассмотрим многообразие их применения. Эпиграфом нашего урока будут слова Бернардо Больцано “Формула подчас кажется более мудрой, чем выдумавший ее человек”.

2. Актуализация имеющихся знаний (устная работа).

А) Вспомним формулу синус суммы, косинус суммы и тангенс суммы аргументов:

sin(x +y) = sinxcosy + cosxsiny;
cos(x+y) = cosxcosy – sinxsiny;
tg(x+y) = .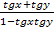

Б) Выполнить задания:

№1 Упростить:

а)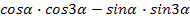
б)
в)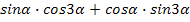
г)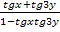

№2 Вычислить:

а)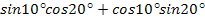
б)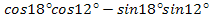
в)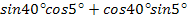
г)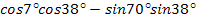
д)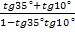

3. Изучение нового материала.

Сейчас мы выведем с вами тригонометрические формулы двойного аргумента и рассмотрим многообразие их применения.

Если положить в формулах, записанных вами в начале урока на доске x= y, то получаем:

1) sin(x+y) = sinxcosy + cosxsiny
sin2x = sinxcosx + sinxcosx = 2sinxcosx

2) cos(x+y) = cosxcosy – sinxsiny
cos2x = cosxcox – sinxsinx = cos²x – sin²x

3) tg(x+y) =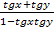
tg2x =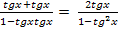

Рассмотреть варианты применения данных формул.

sin10x = 2sin5x*cos5x

sin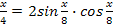

cos(8x – 14y) = cos²(4x – 7y) – sin²(4x – 7y)

tg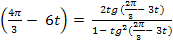

2sin7xcos7x = sin14x

cos²3,5t - sin²3,5t = cos7t

А теперь докажем два тождества, используя доказанную в начале урока формулу cos 2x = cos ²x – sin²x

1. Доказать тождество:

cos2x = 1 – 2sin²x
cos2x = cos²x – sin²x = (1 - sin²x) - sin²x = 1 - 2 sin²x
cos2x = 1 - 2 sin²x

2. Доказать тождество:

cos2x = 2cos²x – 1
cos2x = cos²x – sin²x = cos²x – (1 - cos²x) = 2cos²x – 1
cos2x = 2cos²x – 1

3. Выразить sin²x из равенства:

cos2x = 1 - 2sin²x
2 sin²x = 1 – cos2x
sin²x =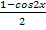

4. Выразить cos²x из равенства:

cos2x = 2cos²x – 1
cos2x+1 = 2cos²x
2cos²x = cos2x+1
cos²x =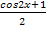

Итак, выполняя №1 и №2, мы получили еще два варианта формулы двойного аргумента, а выполняя №3 и №4, вывели формулы понижения степени.

12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.