ПЕРСПЕКТИВНЫЕ МАСШТАБЫ

ПЕРСПЕКТИВНЫЕ МАСШТАБЫ

Напомню, что в дистанционную точку D у нас сходятся линии, которые в реальности расположены под 45 градусов по отношению к картинной плоскости.

В точку P сходятся линии, которые перпендикулярны картинной плоскости.

В точку F сходятся произвольно расположенные линии по отношению к картинной плоскости.

На картинной плоскости вы изображаем объекты так как они выглядят с учетом перспективных сокращений. Если объект находится на самой картинной плоскости, но он изображается в натуральную величину. Получается, картинная плоскость - это начало отсчета до объекта, находящегося на каком-то расстоянии от человека.

Все размеры предметов, изображенных в перспективе, определяют с помощью перспективных масштабов.

Для определения величины отрезка горизонтальной прямой линии, расположенной параллельно картинной плоскости, применяют масштаб широт.

Рассмотрим применение масштаба широт:

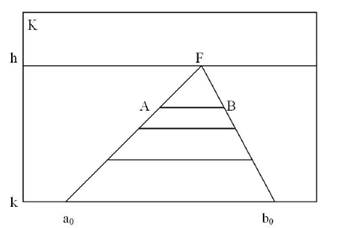
Любой отрезок, например АВ, расположенный между параллельными прямыми Аа0 и Вb0, будет равен отрезку а0b0.

На картинке выше, стрелками обозначены линии, которые в реальности одинаковой величины, но в перспективе, по мере отдаления от человека (картинной плоскости) они сокращаются. Но лишь линия, которая находится на основании картинной плоскости и есть натуральная величина отрезка АВ.

Таким образом, для определения натуральной величины отрезка горизонтальной прямой линии, расположенной параллельно картинной плоскости, необходимо задать на линии горизонта точку схода параллельных прямых (точка F выбирается произвольно). Затем из точки F провести прямые через концы отрезка до пересечения с картинной плоскостью.

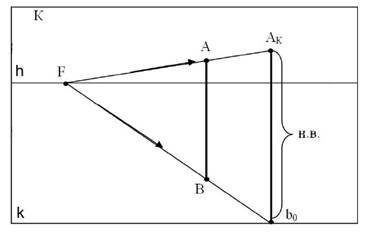
Масштаб высот применяют для определения натуральной величины отрезка прямой, расположенной перпендикулярно предметной плоскости. Рассмотрим пример определения натуральной величины вертикального отрезка АВ (точка В принадлежит предметной плоскости). Параллельные прямые, исходящие из предельной точки F (предельная точка выбрана произвольно), проходят через концы отрезка АВ и пересекаются с картинной плоскостью в точках АК и b0. Величина полученного отрезка АК b0 соответствует натуральной величине отрезка АВ.

И снова, для того, чтобы определить натуральную величину высоты отрезка, мы доводили линии до основания картинной плоскости.

Масштаб глубин применяют для определения натуральной величины отрезка горизонтальной прямой, расположенной перпендикулярно картинной плоскости (т. е. для глубинных прямых). Точка схода для глубинных линий является т.Р.

Параллельные прямые, с помощью которых величину отрезка глубинной прямой выносят на картинную плоскость, необходимо проводить из предельной точки D (дистанционной точки. Она находится от т.Р на расстоянии равном 2 высоты картинной плоскости, либо 1,5 диагонали картинной плоскости). Указанные прямые из т. D (изображенные на рисунке ниже) проходят через концы отрезка АВ и пересекаются с основанием картины в точках а0 и b0. Величина полученного отрезка а0b0 соответствует натуральной величине отрезка АВ.

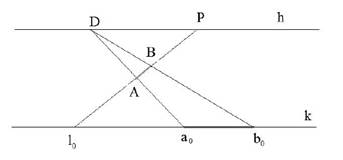
При помощи глубинного масштаба мы также можем определить на каком расстоянии от человека находится линия АВ (То есть расстояние loА). На картинке выше, loА, в перспективе, равно длине loao на основании картинной плоскости. Это и есть натуральная величина.

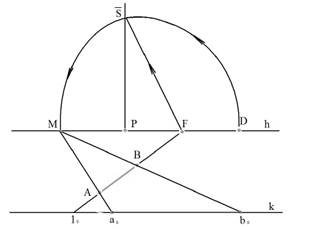
Рассмотрим применение масштаба для отрезка, принадлежащего горизонтальной прямой произвольного направления АВ (для линий, лежащих под произвольным углом точка схода на горизонте F). Для того, чтобы нам найти натуральную величину, нам понадобиться масштабная точка М.

Чтобы определить положение масштабной точки М на линии горизонта необходимо:

1. на линии горизонта поставить точку Р и определить положение дистанционной точки D (она равна от точки Р двум высотам картинной плоскости, либо 1,5 диагонали).

2. выполняют построение совмещенной точки зрения S на линии главного вертикала (PD=PS).

3. Предельную точку заданной прямой F соединяют с совмещенной точкой зрения S и полученным радиусом проводят дугу до линии горизонта (FS=FM). Получаем точку М.

4. Из масштабной точки проводим две линии до основания картинной плоскости через концы отрезка АВ. Получаем на основании картинной плоскости натуральную величину отрезка, лежащего под произвольным углом.

ЗАДАНИЕ 1. Начертить картинную плоскость. Нанести все необходимые обозначения, определить положение дистанционной точки относительно т.Р. В любом месте поставить точку А. Определите расстояние от картинной плоскости до точки А.

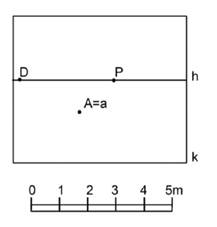
ЗАДАНИЕ 2. Начертить картинную плоскость. Нанести все необходимые обозначения, определить положение дистанционной точки относительно т.Р. Определите расстояние между вертикальными отрезками Аа и Вb.

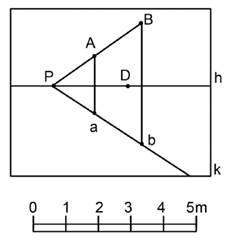
ЗАДАНИЕ 3. Сравните величину вертикальных отрезков Аа и Вb.

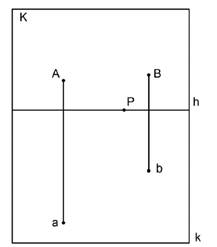
ЗАДАНИЕ 4. На прямой OF от точки А отложите отрезок АВ, равный отрезку СЕ. Обратите внимание, что СЕ находится в глубине пространства, это значит, что сначала надо найти его натуральную величину.

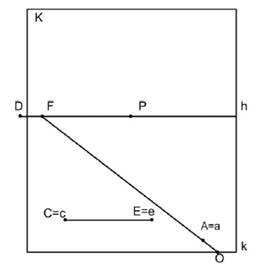
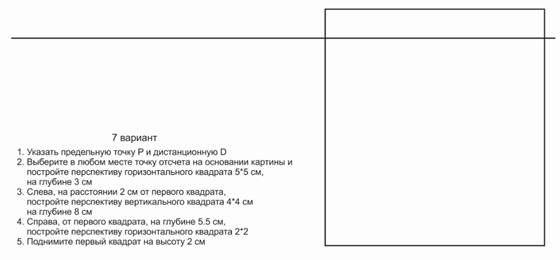
ЗАДАНИЕ 5.