
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ. ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ. имени Гагарина Ю.А.. Контрольная/курсовая. наименование дисциплины). полное название темы или номер варианта). в университет____. Дата регистрации работы. в унив
САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
имени Гагарина Ю.А.

 Факультет ИнЭТиП Курс 3
Факультет ИнЭТиП Курс 3
 Специальность б-ИКТСипу-31
Специальность б-ИКТСипу-31

 Шифр 182908 Вариант 8
Шифр 182908 Вариант 8
Контрольная/курсовая
 работа № 1
работа № 1

 по методам математической физики
по методам математической физики
(наименование дисциплины)
На тему__________________________________
(полное название темы или номер варианта)
 Студента Чувашов Александр Николаевич
Студента Чувашов Александр Николаевич
 (фамилия, имя и отчество полностью)
(фамилия, имя и отчество полностью)
Дата отправки работы Отметка о зачете работы:
в университет____________________________________________
Дата регистрации работы
в университете______________________________
__________________________________
Задача 1. Определить тип уравнения и привести его к каноническому виду.
1.10. 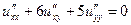 .
.
Решение.
Коэффициенты при  ,
, 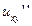 ,
, 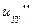 :
: 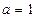 ,
, 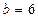 ,
, 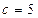 .
.
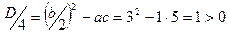 , уравнение – гиперболического типа.
, уравнение – гиперболического типа.
Характеристическое уравнение: 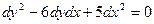 ,
, 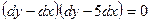 .
.
Корни характеристического уравнения: 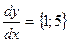 .
.
Составим уравнения характеристик:
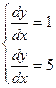 ,
,  ,
, 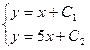 – общие интегралы.
– общие интегралы.
Приведём уравнение к каноническому виду. Подстановки: 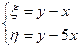 .
.
Выражаем производные: 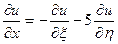 ,
, 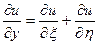 ,
,
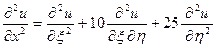 ,
, 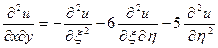 ,
, 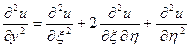 .
.
В новых переменных уравнение приобретает вид:
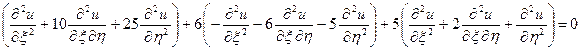 ,
,
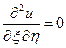 – уравнение в каноническом виде.
– уравнение в каноническом виде.
Общее решение: 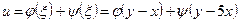 ,
,
где 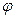 ,
, 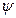 – произвольные дифференцируемые функции.
– произвольные дифференцируемые функции.
Задача 2. Найти решение 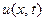 уравнения
уравнения 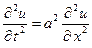 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 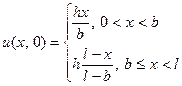 ,
, 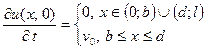 ,
, 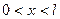
и граничным условиям 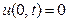 ,
, 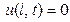 ,
, 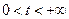 ,
,
| № | 
| 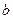
| 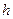
| 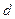
|
| 2.10. | 5,00 | 0,90 | 1,8450 | 2,90 |
Решение.
Разделяем переменные. 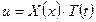 ,
, 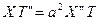 ,
, 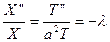 .
.
Задача Штурма-Лиувилля: 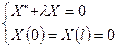 .
.
Характеристическое уравнение: 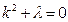 .
.
1) Если 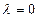 , то
, то 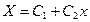 ,
, 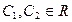 .
.
Подставляем граничные условия: 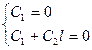 ,
, 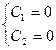 .
.
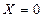 – решение тривиально.
– решение тривиально.
2) Если 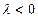 , то
, то 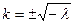 .
. 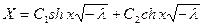 .
.
Граничные условия: 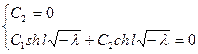 ,
, 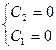 .
. 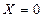 .
.
3) Если 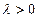 , то
, то 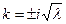 .
. 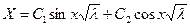 .
.
Граничные условия: 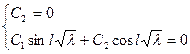 ,
, 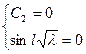 .
.
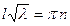 .
. 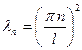 ,
, 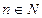 .
.
Пространственный базис: 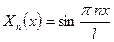 ,
, 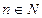 .
.
Разложим начальные условия по базису.
1) 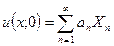 .
. 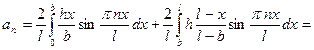
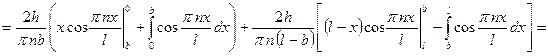

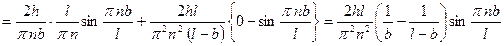 .
.
2) 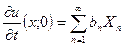 .
. 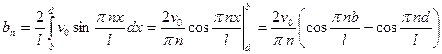 .
.
Ищем решение в виде: 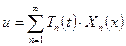 .
.
Приходим к системе дифференциальных уравнений: 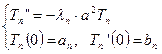 .
.
Общее решение дифференциального уравнения 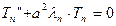 :
:
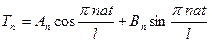 ,
, 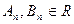 .
.
Производная: 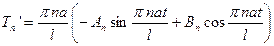 .
.
Подставим начальные условия: 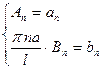 ,
, 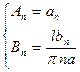 .
.
Окончательно,
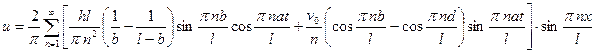 .
.
Задача 3. Методом Фурье найти решение 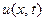 уравнения
уравнения 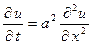 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 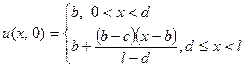 ,
, 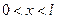
и граничным условиям 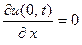 ,
, 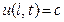 ,
, 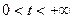 .
.
| № | 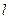
| 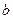
| 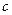
| 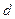
|
| 3.10. | 2,0 | 2,0 | 8,0 | 0,40 |
Решение.
Замена функции: 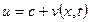 . Задача приобретает вид:
. Задача приобретает вид:
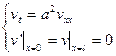 ,
, 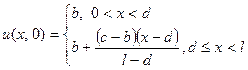 .
.
Разделяем переменные. 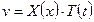 ,
, 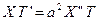 ,
, 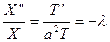 .
.
Задача Штурма-Лиувилля: 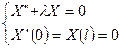 .
.
Характеристическое уравнение: 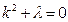 .
.
1) Если 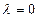 , то
, то 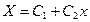 ,
, 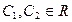 .
.
Подставляем граничные условия: 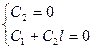 ,
, 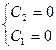 .
.
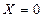 – решение тривиально.
– решение тривиально.
2) Если 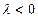 , то
, то 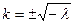 .
. 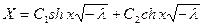 .
.
Граничные условия: 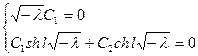 ,
, 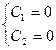 .
. 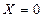 .
.
3) Если 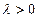 , то
, то 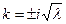 .
. 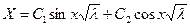 .
.
Граничные условия: 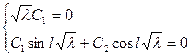 ,
, 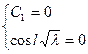 .
.
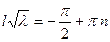 .
. 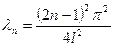 ,
, 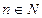 .
.
Пространственный базис: 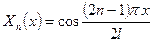 ,
, 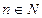 .
.
Разложим начальное условие по базису. 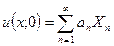 .
.
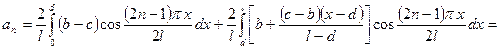
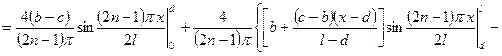
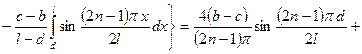
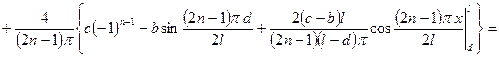
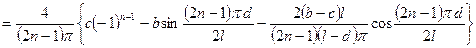 .
.
Ищем решение в виде: 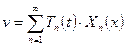 .
.
Приходим к системе дифференциальных уравнений: 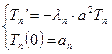 .
.
Общее решение дифференциального уравнения 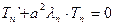 :
:
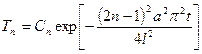 ,
, 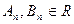 .
.
Подставим начальное условие: 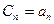 .
.
Окончательно, 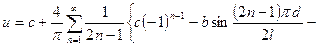
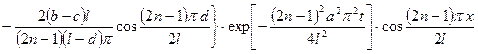 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|