Вариант № 8. Список литературы

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени Гагарина Ю.А. Институт __ИнЭТиП________ Курс_________3__________ Специальность__б-ИКТСипу31____ Шифр_______182888________ Вариант______8_________ Контрольная/курсовая работа №___________________1_______________________ по ________Методам математической физики___________ (наименование дисциплины) На тему____________________________________________ (полное название темы или номер варианта) Студента Краева Алексея Валерьевича______ (фамилия, имя и отчество полностью) ___________________________________________ Дата отправки работы Отметка о зачете работы: в университет_______________________________________ Дата регистрации работы_____________________________ в университете ______________________________________ ______________________________________

Вариант № 8

Задача 1. Определить тип уравнения и привести его к каноническому виду.

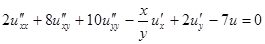Определим коэффициент уравнения.

А=2: B=4: C=10

Тип уравнения определим по знаку:

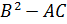
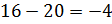
Это эллиптическое уравнение во всей плоскости x,y.

Чтобы привести его к каноническому надо записать для него характеристическое уравнение, в нашем случае:

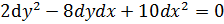или

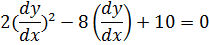
Решим как квадратное уравнение:

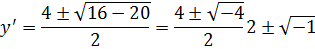
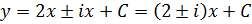
Введём характеристические переменные как вещественную и мнимую часть, одного из интегралов:

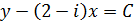
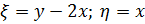
Теперь пересчитаем производные входящие в исходное выражение:

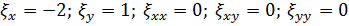
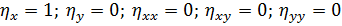
Пересчитаем производные для новых переменных как для сложной функции:

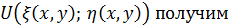
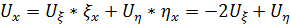
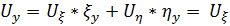
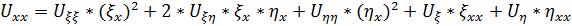
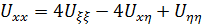
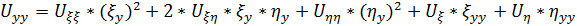
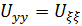
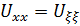
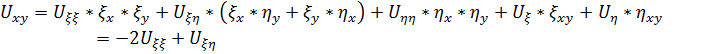
Подставим в исходное уравнение и сгруппируем подобное слагаемые, то получим:

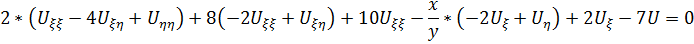
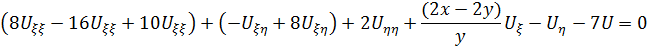
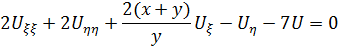
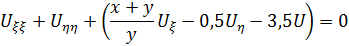
Ответ: Это уравнение эллиптического типа во всей плоскости xoy. Канонический вид при: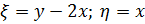

Задача 2.Найти решение 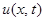уравнения 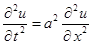, удовлетворяющее начальным условиям

, ,

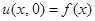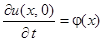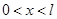
и граничным условиям

, , ,

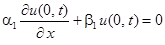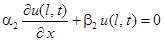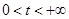где 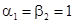, 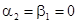для нечётных вариантов; 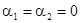, 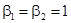для чётных вариантов. Вид функци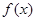й и 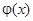изображён на рисунках.

№
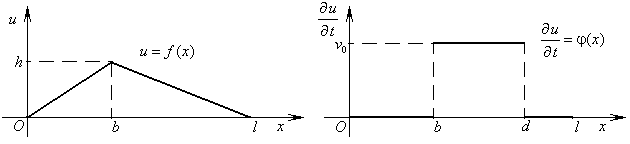
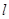
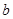
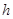
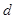
2.8	5,00	2,90	3,0450	4,90

Решение:

Запишем аналитические выражения для функци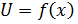й и 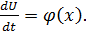Уравнение для прямой проходящей через точку 0 и имеющей угловой коэффициент 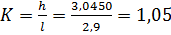имеет вид 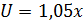, аналогично запишется прямая проходящая через точки (2,9; 3,045) и (0,5) и имеющая угловой коэфф.

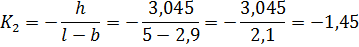
т.о,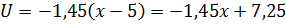

Следовательно, начальные условия имеют вид:

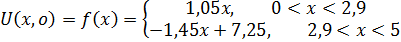
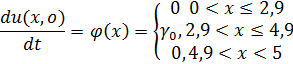
Решать уравнение:

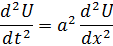
Будем решать методом Фурье (метод разделения переменных). Т.е представим 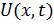– в виде произведения двух функций одна зависит только от x, а другая только от t.

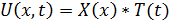
Тогда дважды диффер-мые подставим в исходное уравнение и получим:

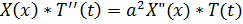
Разделим переменные

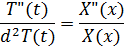
Левая часть не зависит от x, а правая не зависит от t, а это возможно если левая и правая часть константы: т.е

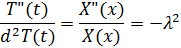
А получаем 2 уравнения:

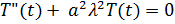
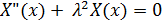
Удовлетворим X(x) граничным условиям X’(0)=0; X(5)=0 и найдем такие значения 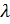при которых существуют отличные от нуля решения уравнения для нахождения общего решения уравнения поставим характеристическое уравнение.

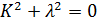
Корнями этого уравнения является:

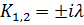
След. Общее решение имеет вид:

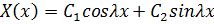
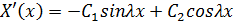
Сопоставим это решение с графическими условиями и получим:

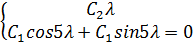
Решая систему получим:

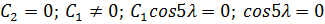
А это возможно в случае 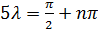т.е значение 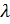при которых задача имеет не тривиальные решения.

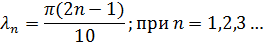
Тогда решения этой задачи имеет вид:

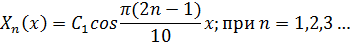
Найдём теперь общее решение для уравнения. При 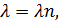для этого составим характеристическое уравнение:

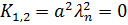
Корнями этого уравнения будут:

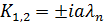
И след. Общее решение будет иметь вид:

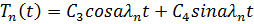
Подставляем в это выражение:

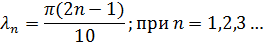
Получаем:

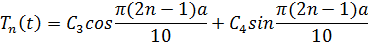
B тогда подставим в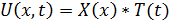

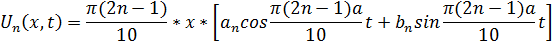
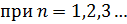
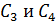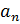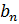Каждому значению n отвечают свои постоянные поэтому пишем и , а 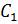также включаем в 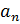и 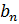. Так как уравнение линейное и однородное, то функция:

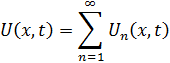
Является решением уравнения 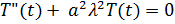удовлетворяет граничным условиям.

Определим 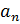и 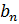чтобы решения удовлетворяло и начальным условиям, то есть.

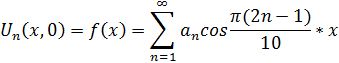
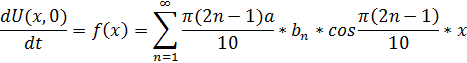
Эти функции в промежутке (0,5) различаются в ряд Фурье по косинусам и тогда:

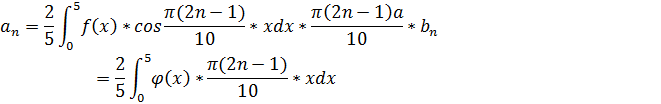
Подставляя выражение для функции 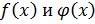, получим:

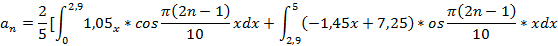
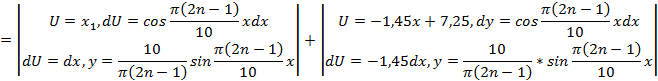
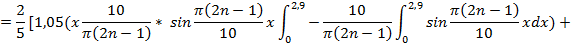
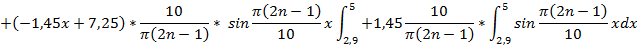
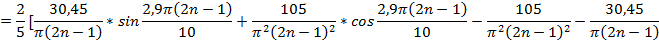
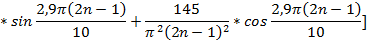
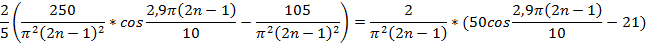
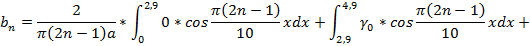
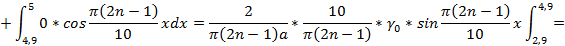
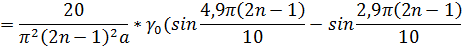
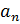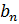Найденные выражения и подставим в искомое выражение и получим:

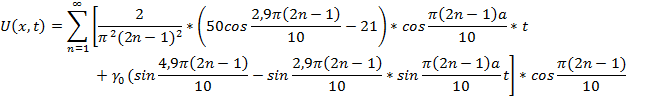
Ответ:Удовлетворяющее требованиям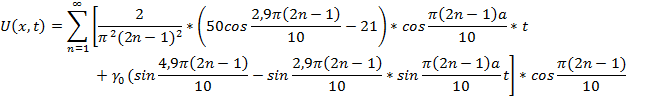

Задача 3. Методом Фурье найти решение 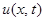уравнения 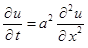, удовлетворяющее начальному условию

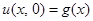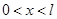
и граничным условиям

, , ,

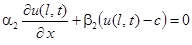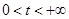где 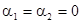, 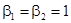для нечётных вариантов; 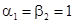, 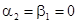для чётных вариантов. Вид функции 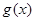изображён на рисунке.

№
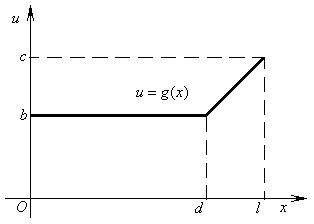
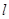
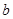
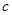
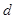
8.	2,0	4,0	18,0	1,20

Решение

Найдём аналитическое выражение функции 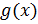. Функция 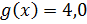при 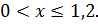В интервале 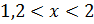запишем 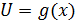в виде прямой, проходящей через точку 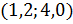и имеющей угловой коэффициент:

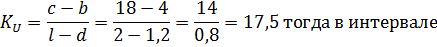
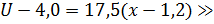
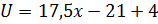
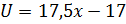
С учётом полученных выражений начальное условие запишем в виде:

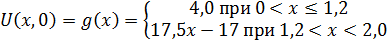
Так как граничные условия не нулевые, то метод Фурье для решения этой задачи не применим. Поэтому введем новую функцию:

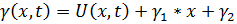
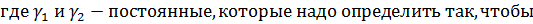
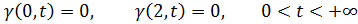
И так,

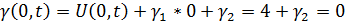
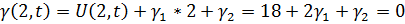
Из системы уравнений:

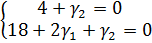
Получим: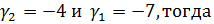

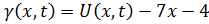
Подставляя функцию 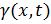в уравнение, получим:

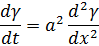
А начальные и граничные условия примут вид:

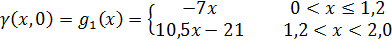
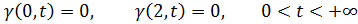
Теперь для решения этой краевой задачи можно применить метод Фурье, пусть: 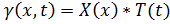, тогда подставляя в уравнение 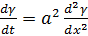и разделяя переменные, получим:

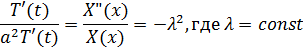
Из этого равенства получаем два уравнения:

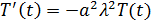
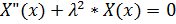
Общее решение этих уравнение имеет вид:

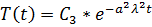
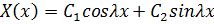
Для нахождения 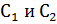воспользуемся граничными условиями

Подставим в решение 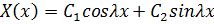граничные условия:

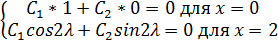
Решая эту систему и учитывая, что ищется не нулевое решение задачи Штурма - Лиувилля получим:

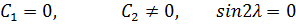
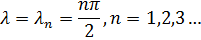
Найденным собственным значениям 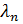задачи соответствуют собственные функции

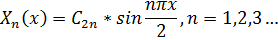
Общее решение уравнения 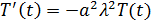при 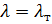примет вид:

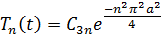
Тогда в соответствии с представлением решения 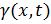в виде : 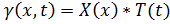, получим частные решения в виде:

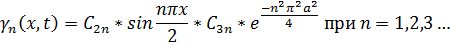
Запишем теперь решение краевой задачи:

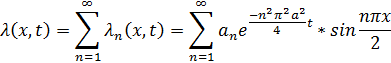
Где 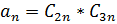– пока неизвестные постоянные, определяемые из начального условия. Полагая t=0 в 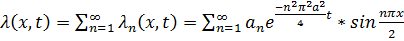и учитывая 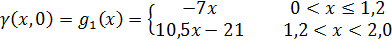, получим

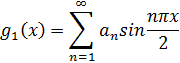
Отсюда найдем коэфф. 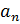этого тригонометрического ряда Фурье:

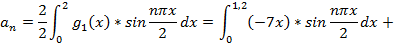
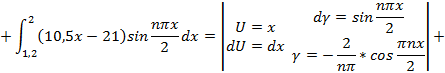
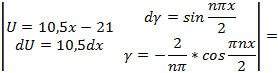
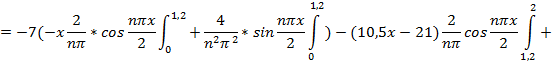
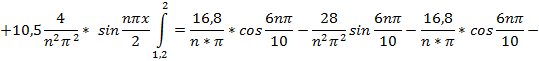
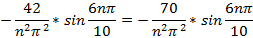
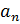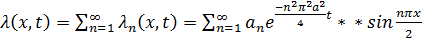Подставляя найденные значения в и учитывая 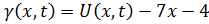получим:

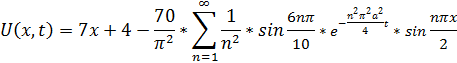
Ответ: решение 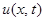уравнения 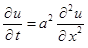, удовлетворяющее начальному условию: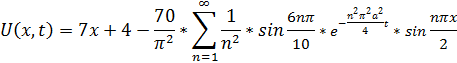

Список литературы

1. Акимов, О.Е. Дискретная математика. Логика, группы, графы / О.Е. Акимов. - М.: Бином. Лаборатория знаний, 2009. - 376 c.

2. Акимов, О.Е. Дискретная математика. Логика, группы, графы / О.Е. Акимов. - М.: Бином. Лаборатория знаний, 2003. - 376 c.

3. Андерсон, Дж. Дискретная математика и комбинаторика / Дж. Андерсон. - М.: Диалектика, 2019. - 960 c.

4. Асанов, М.О. Дискретная математика: графы, матроиды, алгоритмы: Учебное пособие / М.О. Асанов, В.А. Баранский, В.В. Расин. - СПб.: Лань, 2010. - 368 c.

5. Бабичева, И.В. Дискретная математика. Контролирующие материалы к тестированию: Учебное пособие / И.В. Бабичева. - СПб.: Лань, 2013. - 160 c.

6. Баврин, И.И. Дискретная математика для педагогических вузов: Учебник и задачник для прикладного бакалавриата / И.И. Баврин. - Люберцы: Юрайт, 2015. - 208 c.

7. Баврин, И.И. Дискретная математика: Учебник и задачник для СПО / И.И. Баврин. - Люберцы: Юрайт, 2016. - 209 c.

8. Вороненко, А.А. Дискретная математика. Задачи и упражнения с решениями: Учебно-методическое пособие / А.А. Вороненко. - М.: НИЦ Инфра-М, 2013. - 104 c.

9. Вороненко, А.А. Дискретная математика. Задачи и упр. с реш.: Учебно-методическое пособие / А.А. Вороненко, В.С. Федорова. - М.: Инфра-М, 2018. - 160 c.

10. Галкина, В.А. Дискретная математика: комбинаторная оптимизация на графах / В.А. Галкина. - М.: Гелиос АРВ, 2003. - 232 c.