Геометрия 8 класс. Прикладная геометрия. Решение.. Решение.

Геометрия 8 класс

Урок 11 - 12

Прикладная геометрия

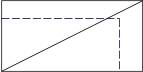
У крестьянина было кукурузное прямоугольное поле. Его диагональ равна 100 метров. И всё у этого крестьянина было хорошо, пока не наступил кризис и государство не пришло национализировать это поле. К его счастью, власти потребовали лишь часть: «Уменьши одну сторону своего прямоугольного поля на 50 м, а другую — на 62 м. Оставшаяся часть твоя.» После подсчётов, у крестьянина получилось, что периметр поля уменьшился в 5 раза. Найдите диагональ нового поля.

Решение.

Пусть исходные стороны поля равны a и b. Из условия задачи можно составить систему уравнений:

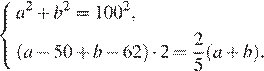
Решим ее:

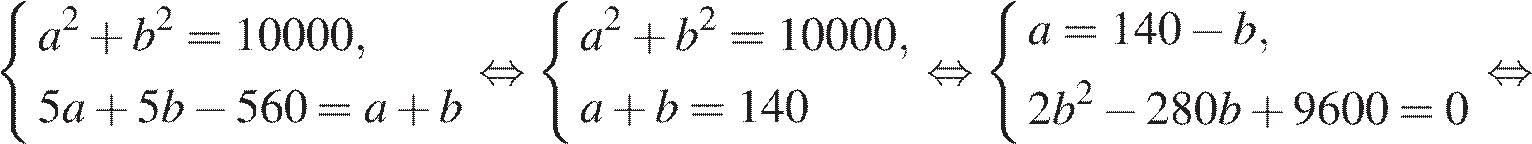
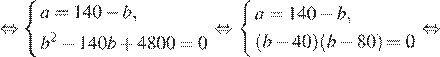
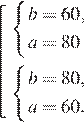
Найдем новую диагональ по теореме Пифагора:

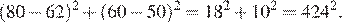
Таким образом, новая диагональ стала равна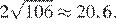

Ответ:

Лист жести имеет форму прямоугольника, длина которого на 10 см больше ширины. По углам этого листа вырезали квадраты со стороной 5 см и сделали коробку. Найдите размеры листа жести в сантиметрах, если объем коробки равен 1000 см³. Объем коробки равен произведению ее длины, ширины и высоты.

Решение.

Примем стороны прямоугольника за a см и b см. После вырезания его стороны стали равны 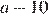см и 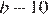см. Высота коробки — 5 см. Из условия задачи составим систему уравнений:

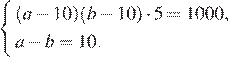
Решим её методом подстановки:

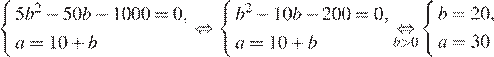
Таким образом, ширина и длина листа жести равны 20 и 30 сантиметров соответственно.

Ответ: 20 и 30.

20 и 30.

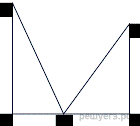
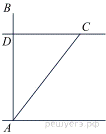
Две башни, одна высотой 40 футов, а другая — 30 футов, расположены на расстоянии 50 футов одна от другой. К расположенному между ними колодцу слетают одновременно с обеих башен две птички, и летя с одинаковой скоростью, одновременно прибывают к колодцу. Найти расстояние от колодца до башен в футах.

4. Решение.

Пусть точка M — место расположения колодца. Тогда сумма отрезков AM и MC равна 50 футов. Примем эти отрезки за a и b соответственно. Факт того, что птицы прилетели одновременно, летя с одинаковой скоростью означает, что отрезки BM и DM равны. Составим систему уравнений и решим её.

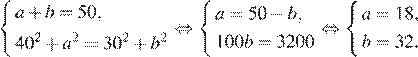
Таким образом, расстояние равно 18 и 32 футов соответственно.

Ответ: 18 и 32.

18 и 32.

Цветок Лотоса возвышается над тихим озером на полфута. Когда порыв ветра отклонил цветок от прежнего места на 2 фута, цветок скрылся над водой. Определите глубину озера в футах.

5. Решение.

Примем глубину пруда за x, а длину лотоса за y. Из условия 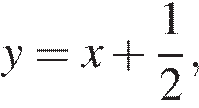а 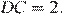Так как 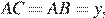составим систему уравнений и решим ее

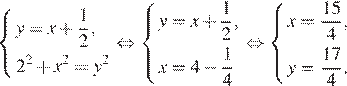
Таким образом, получаем, что глубина озера равна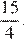

Ответ: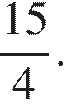

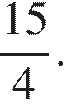
55.

Длина садового участка, имеющего форму прямоугольника, на 10 м больше его ширины. Его площадь решили увеличить на 400 м. Для этого длину увеличили на 10 м, а ширину — на 2 м. Найдите площадь нового участка в м².

Решение.

Примем длину и ширину садового участка за a и b. Из условия задачи составим систему уравнений и решим её

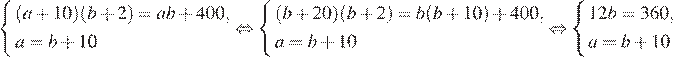
Откуда получаем, что до увеличения участка его ширина и длина были равны 30 и 40 соответственно. Таким образом, площадь старого участка равна 1200 м², а нового — 1600 м².

Ответ: 1600.

1600.

Для школьной площадки выделен прямоугольный участок земли определенной площади. Если его заменить квадратным участком той же площади , то потребуется меньше материала для его отгораживания. Для этого надо длину участка уменьшить на 12 м, а ширину увеличить на 10 м. Чему равна сторона квадратного участка в метрах?