
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Геометрия
Геометрия
Дата:02.04.20 г.
Тема:Соотношения между сторонами и углами треугольника
1. Повторение. Вспоминаем:
Теорема: В треугольнике против большей стороны лежит больший угол и, обратно, против большего угла лежит большая сторона.
Следствие (признак равнобедренного треугольника): Если два угла треугольника равны, то этот треугольник равнобедренный.
2.  Решение задач.
Решение задач.
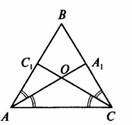
№ 240. Дано:  – равнобедренный,
– равнобедренный,
АС – основание АА1 и СС1 – биссектрисы.
Доказать:  – равнобедренный.
– равнобедренный.
Доказательство:
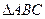 – равнобедренный с основанием АС. В равнобедренном треугольнике углы при основании равны, следовательно,
– равнобедренный с основанием АС. В равнобедренном треугольнике углы при основании равны, следовательно, 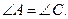
АА1 и СС1 – биссектрисы двух равных углов, значит, 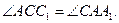 По признаку равнобедренного треугольника
По признаку равнобедренного треугольника 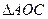 – равнобедренный■
– равнобедренный■
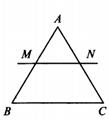
№ 241. Дано: 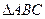 – равнобедренный,
– равнобедренный,
АВ=АС. MN||BC.
Доказать: 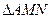 – равнобедренный.
– равнобедренный.
Доказательство:
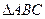 – равнобедренный, АВ=АС, значит,
– равнобедренный, АВ=АС, значит, 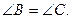
MN||BC, следовательно, 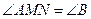 и
и 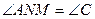 как соответственные. Тогда,
как соответственные. Тогда, 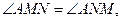 т.е. в
т.е. в 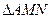 два угла равны. По признаку равнобедренного треугольника
два угла равны. По признаку равнобедренного треугольника  – равнобедренный■
– равнобедренный■
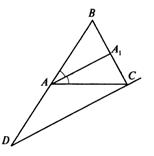
№ 243. Дано:  , АА1 – биссектриса,
, АА1 – биссектриса,
CD||АА1, 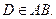
Доказать: АD=АС .
Доказательство:
АА1 – биссектриса, тогда 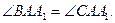
CD||АА1, AC – секущая, значит, 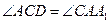 как накрест лежащие.
как накрест лежащие.
CD||АА1, BD – секущая, значит, 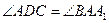 как соответственные.
как соответственные.
Т.е., в 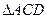
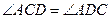 , тогда по признаку равнобедренного треугольника
, тогда по признаку равнобедренного треугольника 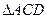 – равнобедренный с основанием CD, значит, АD=АС■
– равнобедренный с основанием CD, значит, АD=АС■
№ 246. Дано: 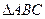 , ВО, СО – биссектрисы, ОЕ||АВ, ОD||АC.
, ВО, СО – биссектрисы, ОЕ||АВ, ОD||АC.
Доказать: 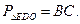
Доказательство:
ВО, СО – биссектрисы, значит, 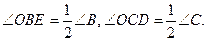
ОЕ||АВ, тогда 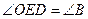 как соответственные.
как соответственные.
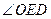 – внешний для
– внешний для 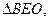 значит,
значит, 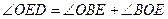 ,
, 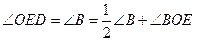 , отукуда
, отукуда 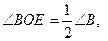 т.е.
т.е. 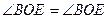 и по признаку равнобедренности ВЕ=ОЕ.
и по признаку равнобедренности ВЕ=ОЕ.
Аналогично, ОD||АC, 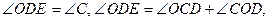
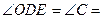
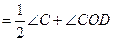 , откуда
, откуда 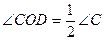 и
и 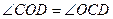 , по признаку равнобедренности СD=OD.
, по признаку равнобедренности СD=OD.
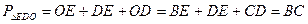 ■
■
№ 247. Дано: 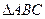 , АВ=АС, AP=AQ.
, АВ=АС, AP=AQ.
Доказать: а) 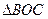 – равнобедренный;
– равнобедренный;
б) АО – медиана и высота.
Доказательство:
а) АВ=АС, т.е. 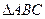 – равнобедренный, значит,
– равнобедренный, значит, 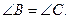
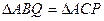 по двум сторонам и углу между ними (АВ=АС, AP=AQ,
по двум сторонам и углу между ними (АВ=АС, AP=AQ, 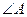 – общий), следовательно,
– общий), следовательно, 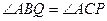 . Тогда
. Тогда 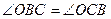 и по признаку равнобедренности
и по признаку равнобедренности 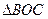 - равнобедренный с основанием ВС.
- равнобедренный с основанием ВС.
б) Т.к. 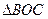 - равнобедренный с основанием ВС, то ВО=СО.
- равнобедренный с основанием ВС, то ВО=СО.
Тогда 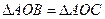 по трем сторонам (АВ=АС, ВО=СО, АО – общая), значит,
по трем сторонам (АВ=АС, ВО=СО, АО – общая), значит, 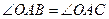 , т.е. АО – биссектриса.
, т.е. АО – биссектриса.
Т.к. 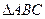 – равнобедренный, АО – биссектриса, проведенная к основанию, значит, АО является и медианой и высотой■
– равнобедренный, АО – биссектриса, проведенная к основанию, значит, АО является и медианой и высотой■
3. Д/з. Решать №№ 242, 244, 245.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|