ГЕОМЕТРИЯ:. А – вершина треугольника АВС!!!

ГЕОМЕТРИЯ:

Основные свойства треугольника:

1) Сумма углов любого треугольника равна 180°.

2) Внешний угол треугольника равен сумме двух других углов не смежных с ним.

3) Высоты, медианы, биссектрисы и серединные перпендикуляры треугольника пересекаются в одной точке (каждые линии в своей точке!)

4) Медианы треугольника точкой пересечения делятся в отношении 2 к 1 считая от вершины.

5) Центром вписанной в треугольник окружности является точка пересечения биссектрис.

6) Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к его сторонам.

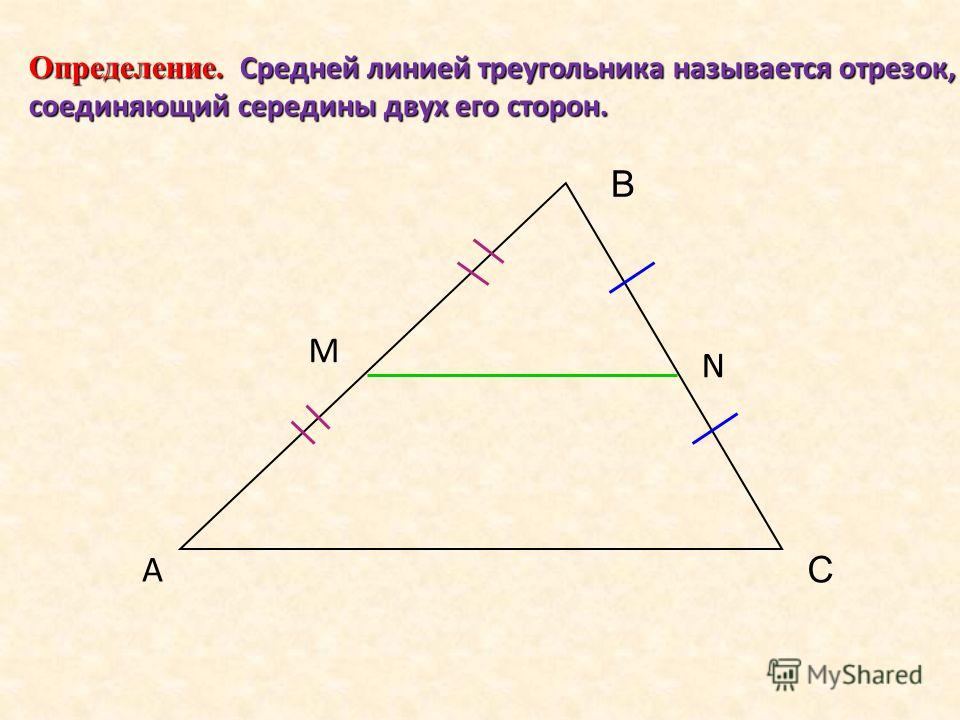
7) Средняя линия треугольника параллельна одной из его сторон и равна ее половине.

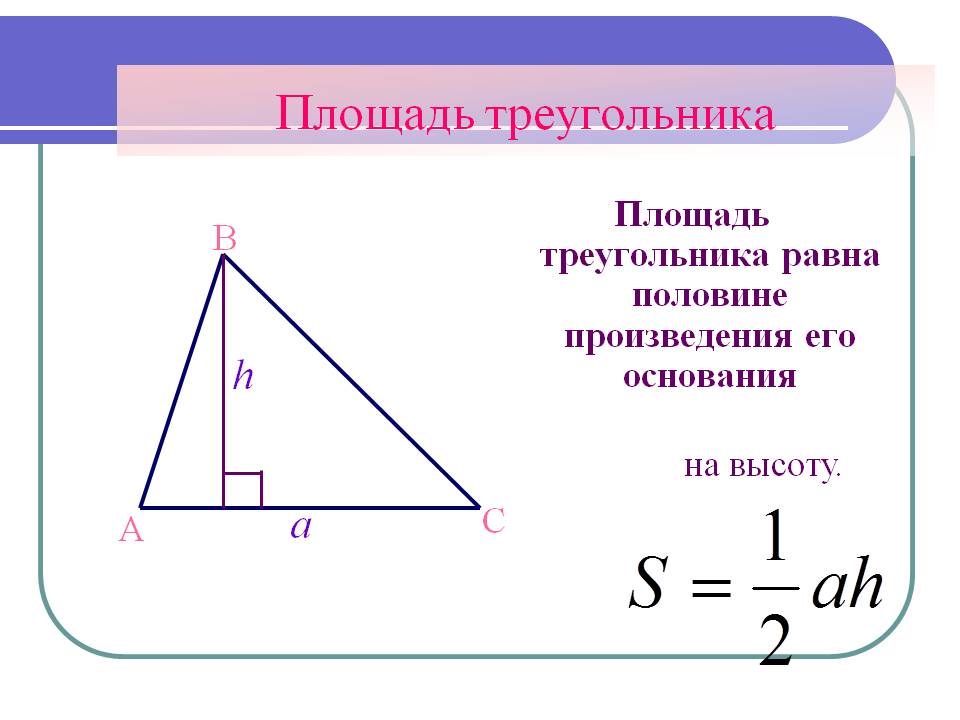
8) Площадь треугольника равна половине произведения высоты на основание.

Основные свойства равнобедренного треугольника:

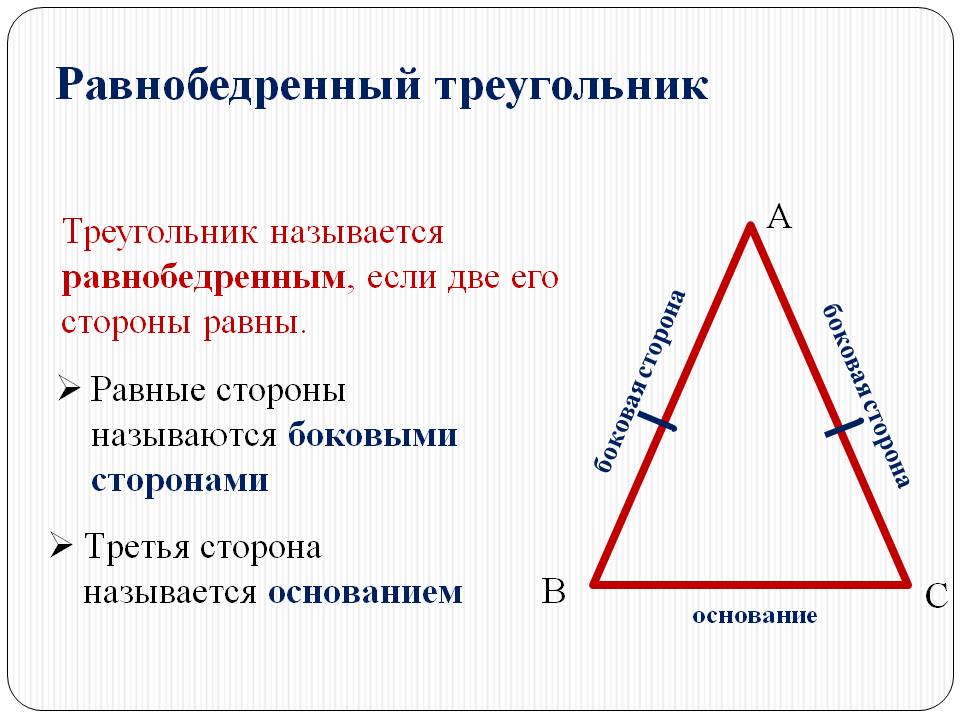
А – вершина треугольника АВС!!!

1) Равнобедренный треугольник обладает всеми свойствами обыкновенного треугольника.

2) Углы при основании равнобедренного треугольника равны.

3) Высота, проведенная из вершины равнобедренного треугольника, является так же его биссектрисой и медианой.

4) Высоты, биссектрисы и медианы, проведенные к боковым сторонам равнобедренного треугольника, равны между собой.

Основные свойства равностороннего (правильного) треугольника:

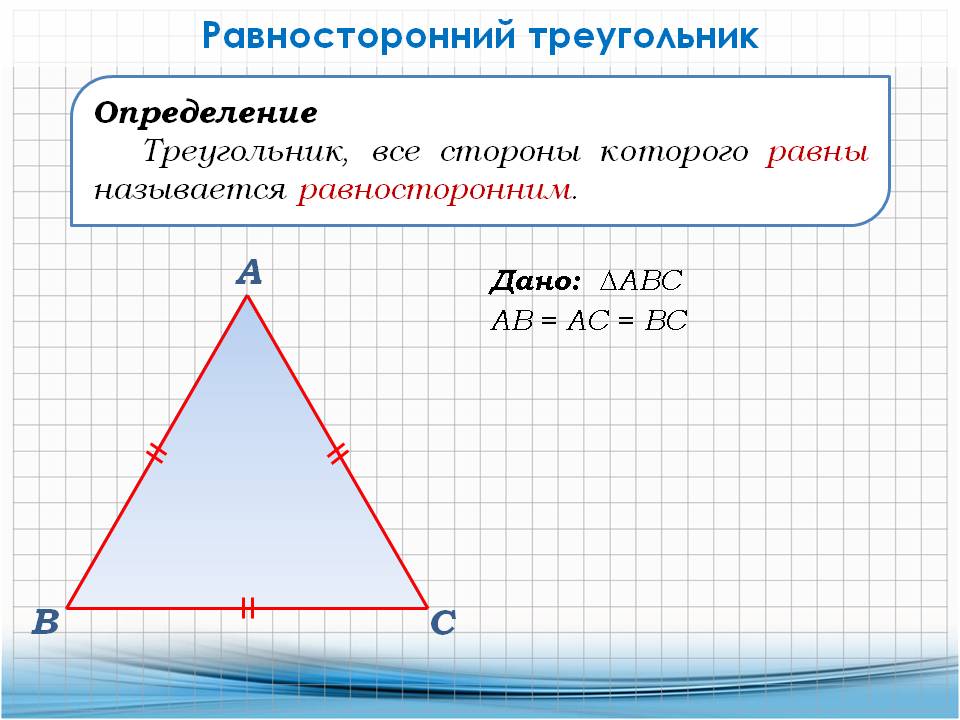
1) Равносторонний треугольник обладает всеми свойствами обыкновенного и равнобедренного треугольника.

2) Углы равностороннего треугольника равны между собой и равны по 60°.

3) Высота, проведенная из любой вершины равностороннего треугольника, является его биссектрисой и медианой.

4) Высоты, медианы, биссектрисы и серединные перпендикуляры к сторонам равностороннего треугольника пересекаются в ОДНОЙ (общей!) точке.

5) Центры вписанной и описанной около равностороннего треугольника окружностей – совпадают.

Основные свойства прямоугольного треугольника:

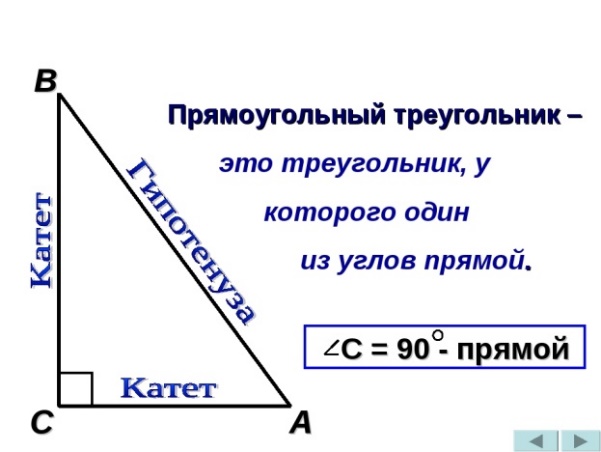
1) Прямоугольный треугольник обладает всеми свойствами обыкновенного треугольника.

2) Сумма острых углов прямоугольного треугольника равна 90°.

3) Катет, лежащий против угла 30°, равен половине гипотенузы.

4) Медиана, проведенная к гипотенузе, равна ее половине.

5) Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы, а сама гипотенуза является диаметром этой окружности.

6) Теорема Пифагора: Квадрат гипотенузы равен сумме квадратов катетов.

7) Чтобы вычислить синус острого угла прямоугольного треугольника, надо противолежащий катет разделить на гипотенузу.

8) Чтобы вычислить косинус острого угла прямоугольного треугольника, надо прилежащий катет разделить на гипотенузу.

9) Чтобы вычислить тангенс острого угла прямоугольного треугольника, надо противолежащий катет разделить на прилежащий катет.

10) Площадь прямоугольного треугольника равна половине произведения его катетов.

Основные свойства параллелограмма:

Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.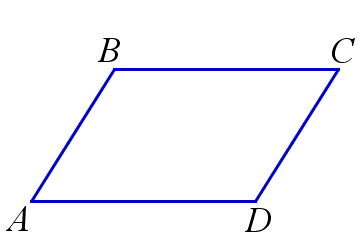

1) Противоположные стороны параллелограмма параллельны и равны.

2) Противоположные углы параллелограмма равны.

3) Сумма всех углов параллелограмма равна 360°.

4) Сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.

5) Диагонали параллелограмма точкой пересечения делятся пополам.

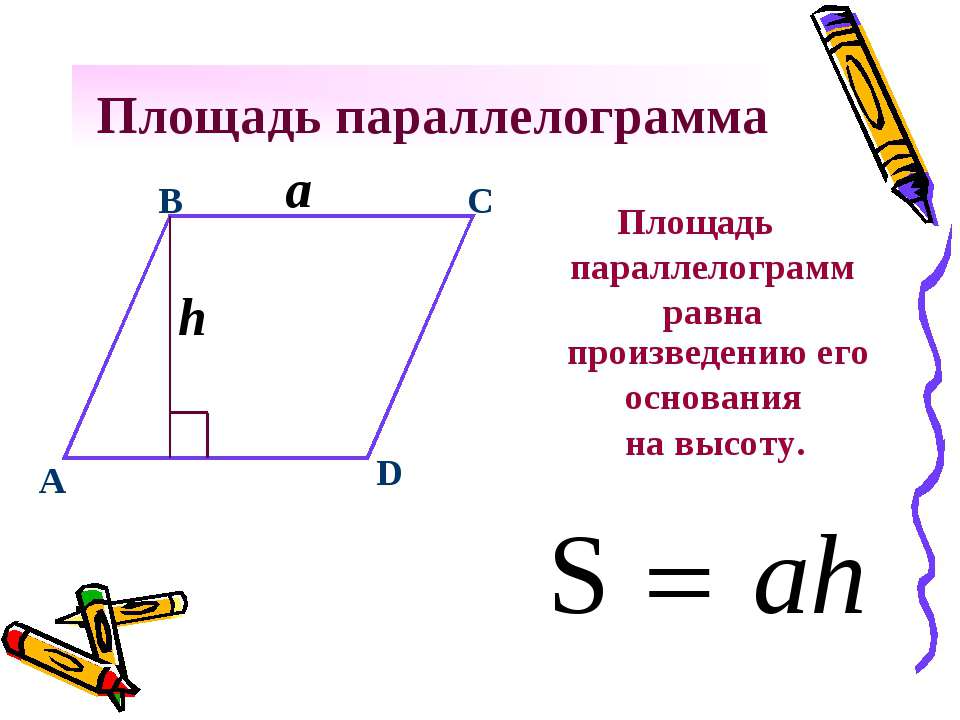
6) Площадь параллелограмма равна произведению высоты на основание.

Основные свойства ромба:

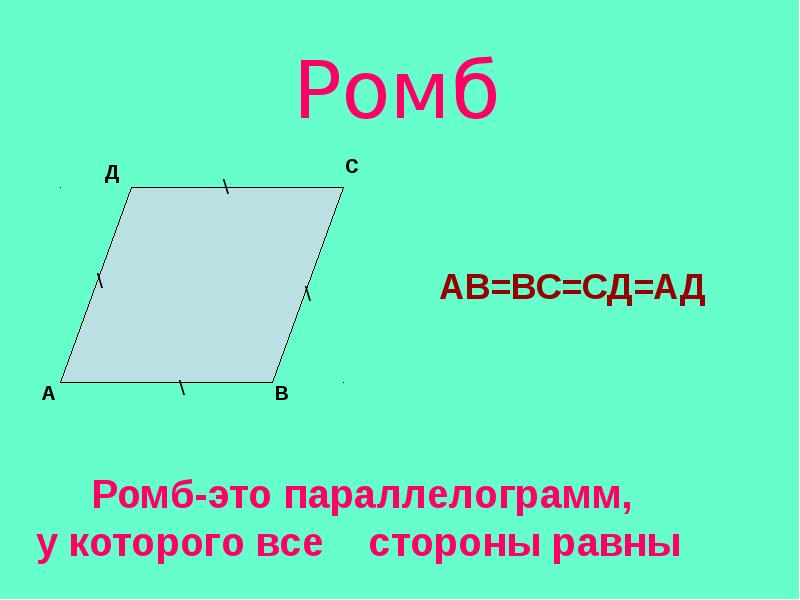
1) Ромб обладает всеми свойствами параллелограмма.

2) Диагонали ромба перпендикулярны между собой.

3) Диагонали ромба делят его углы пополам (являются биссектрисами углов).

4) Площадь ромба равна половине произведения его диагоналей.

Основные свойства прямоугольника:

1) Прямоугольник обладает всеми свойствами параллелограмма.

2) Все углы прямоугольника равны по 90°.

3) Диагонали прямоугольника равны.

4) Площадь прямоугольника равна произведению его смежных сторон (высоты на длину).

Основные свойства квадрата:

1) Квадрат обладает всеми свойствами параллелограмма и ромба.

2) Все стороны квадрата равны и все углы равны по 90°.

3) Площадь квадрата равна квадрату его стороны.

Основные свойства трапеции:

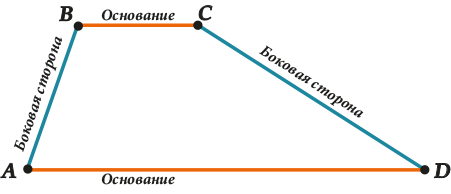
Трапеция – такой четырехугольник, у которого две стороны параллельны, а две другие – нет. Параллельные стороны называются – основания, а непараллельные стороны называются боковыми сторонами.

1) Сумма углов трапеции равна 360°.

2) Сумма углов, прилежащих к боковой стороне трапеции, равна 180°.

3) Площадь трапеции равна полу-сумме оснований, умноженной на высоту.

Основные свойства равнобедренной трапеции:

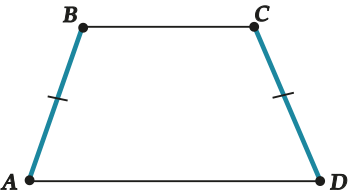
Если боковые стороны равны, то она называется равнобедренной, или равнобокой.

1) Равнобедренная трапеция обладает всеми свойствами обыкновенной трапеции.

2) Углы при основаниях равнобедренной трапеции равны.

3) Диагонали равнобедренной трапеции равны.