- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Паронджанов В. Д. 9 страница
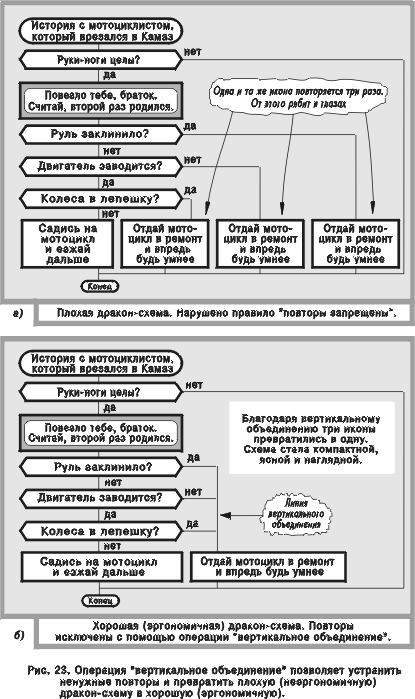
Сравнивая алгоритмы на рис. 23а и б, легко заметить, что схема на рис. 23б обладает более высоким эргономическим качеством: она стала более компактной, ясной и наглядной, поскольку освободилась от бессмысленного повторения икон. Отсюда проистекает вывод: равносильное преобразование “вертикальное объединение” позволяет улучшить эргономичность алгоритмов.
Иногда для исключения повторов используется не вертикальная, а горизонтальная линия. Соответствующая операция называется горизонтальным объединением. Она также является равносильным преобразованием.
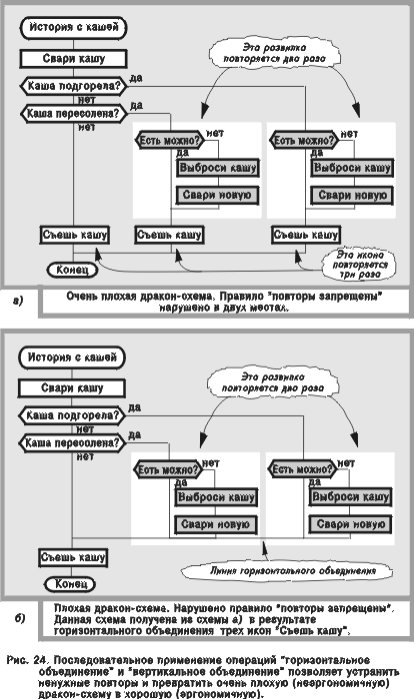
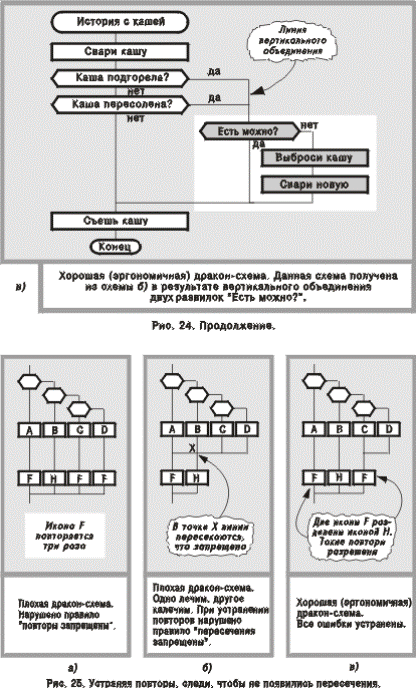
Рассмотрим пример на рис. 24а. Сначала с помощью горизонтального объединения устраним повторение иконы “Съешь кашу” и получим схему на рис. 24б. Затем применим вертикальное объединение и исключим повторение развилки “Есть можно?”. Окончательный результат показан на рис. 24в. Полученная схема более удобна и занимает меньше места, чем исходная схема на рис. 24а.
Разобранный пример показывает, что равносильное преобразование “горизонтальное объединение” также улучшает эргономичность алгоритмов.
П р е д о с т е р е ж е н и е: выполняя вертикальное и горизонтальное объединение, нужно следить, чтобы не появились пересечения соединительных линий (рис. 25).
ЭРГОНОМИЧНОСТЬ ЛИТЕРАЛЬНЫХ АЛГОРИТМОВ
Можно ли улучшить эргономичность литеральных дракон-схем с помощью равносильных преобразований? Мы уже знаем, что рокировка в этом случае бесполезна. Однако вертикальное и горизонтальное объединение позволяют заметно повысить эргономичность литеральных схем.
|

23
|

24
|

24-25
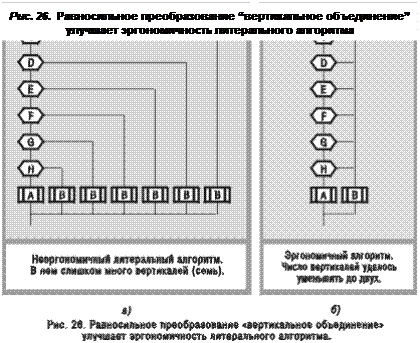
Чтобы убедиться в этом, обратимся к рис. 26 и 27. В самом деле, схема на рис. 26а выглядит неоправданно громоздкой: она содержит семь вертикалей, тринадцать икон и заставляет читателя шесть раз читать идентификатор В, чтобы убедиться, что правые шесть икон одинаковые. А равносильная ей схема на рис. 26б (полученная методом вертикального объединения) свободна от этого недостатка. Она наглядна, проста и изящна, содержит только две вертикали и восемь икон, занимает втрое меньше места на листе бумаги (на экране) и к тому же имеет всего два прямоугольных излома линий (на рис. 26а — семь изломов). Таким образом, литеральная схема на рис. 26б более эргономична, чем ее соседка.
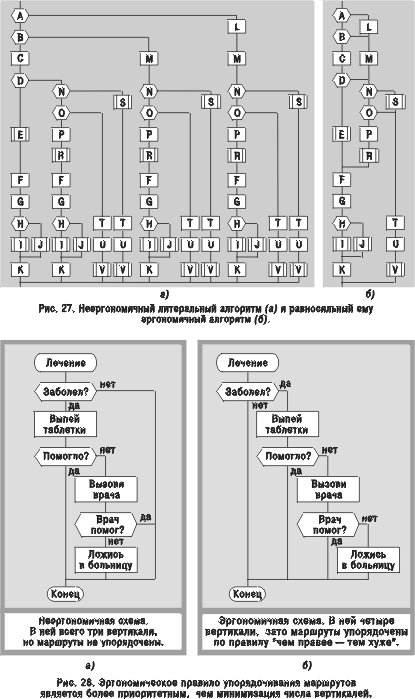
Еще более громоздкой выглядит литеральная схема на рис. 27а, в которой насчитывается 14 вертикалей. А равносильная ей схема на рис. 27б (полученная методом вертикального и горизонтального объединения) снова выигрывает: позволяет уменьшить число вертикалей почти в пять раз (с 14 до 3), сокращает число икон более чем в три раза (с 65 до 21), обеспечивает более экономное топологическое упорядочивание маршрутов, заметно сокращает суммарную длину соединительных линий.
Проведенный анализ позволяет сделать вывод: в отличие от рокировки, которая полезна только для смысловых дракон-схем, вертикальное и горизонтальное объединение улучшают эргономичность не только смысловых, но и литеральных алгоритмов.
|

что делать, если эргономические требования
противоречат друг другу?
До сих пор мы рассматривали простейшие случаи, когда различные эргономические требования не вступали в конфликт. Однако подобные конфликты возможны. Вот два эргономических критерия, которые могут противоречить друг другу:
! правило главного и побочного маршрутов,
! минимизация числа вертикалей.
Чтобы исключить конфликт, следует держаться принципа: правило маршрутов имеет более высокий приоритет, нежели стремление уменьшить число вертикалей.
В качестве иллюстрации сравним равносильные схемы на рис. 28. По критерию “минимизация числа вертикалей” выигрывает схема на рис. 28а, имеющая на одну вертикаль меньше. Однако в ней нарушается правило маршрутов, причем сразу в двух местах. Во-первых, главный маршрут (когда человек здоров) не совмещен с шампуром. Во-вторых, маршруты не упорядочены слева направо, ибо самое тяжелое заболевание (когда человек вынужден лечь в больницу) находится на средней вертикали, а слева и справа от нее находятся более легкие недомогания. Таким образом, схему на рис. 28а нельзя признать эргономичной.
Чтобы исправить недостаток, необходимо выполнить:
! вертикальное разъединение в точке С (эта операция обратна вертикальному объединению);
! рокировку развилки “Заболел?”;
! рокировку развилки “Врач помог?”.
В итоге получим схему на рис. 28б, где все маршруты упорядочены слева направо по принципу “чем правее — тем хуже”. В самом деле, левая вертикаль означает, что дела идут хорошо, ибо человек здоров; значит, главный маршрут идет по шампуру. Вторая вертикаль показывает легкое недомогание, которое можно снять таблеткой. Третья вертикаль говорит: самочувствие ухудшилось, нужен врач. Наконец, четвертая (крайняя правая) вертикаль означает, что дела обстоят плохо — пришлось лечь в больницу.
Как уже упоминалось, схема на рис. 28б не удовлетворяет эргономическому требованию минимизации числа вертикалей. Тем не менее мы признаем ее эргономичной, поскольку выполняется более приоритетное правило маршрутов. Отсюда вытекает, что (благодаря наличию приоритетов) комплекс эргономических требований является взаимоувязанным и непротиворечивым.
ИКОНА-ВСТАВКА КАК ЭРГОНОМИЧЕСКИЙ ПРИЕМ
Мы уже знаем, что язык ДРАКОН запрещает применять пересечения, обрывы и соединители. Отсюда вытекает жесткое ограничение: любая дракон-схема должна целиком размещаться на одном листе бумаги. А если она слишком большая и вылезает за рамки прокрустова ложа?
Тогда можно взять бумагу больших размеров, например формата А1. А если схема громадная и все равно не помещается? На этот случай предусмотрены специальные приемы, позволяющие уменьшить габариты дракон-схемы и разрубить ее на куски. Эти приемы позволяют разместить дракон-схему на листах желаемого размера. Рассмотрим проблему на “миниатюрном” примере.
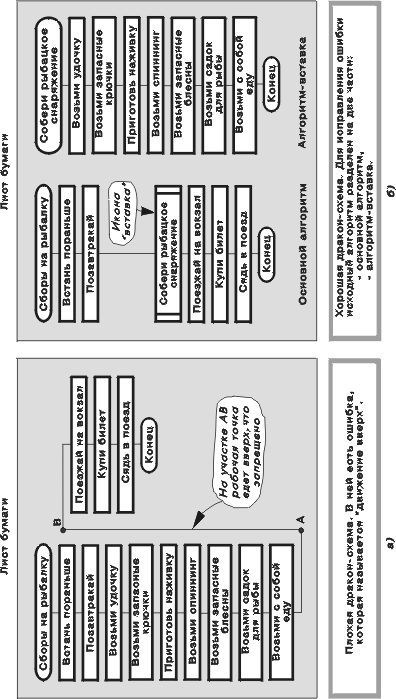
Предположим, линейный алгоритм состоит из четырнадцати икон, а бумажный лист небольшой, так что на нем можно разместить по вертикали не более десяти икон. Как быть?
На рис. 29 показаны два варианта решения проблемы. Алгоритм на рис. 29а не годится, так как на участке АВ рабочая точка движется вверх, что запрещено правилами языка ДРАКОН. Преодолеть затруднение можно двумя способами: применить конструкцию “силуэт” (о которой шла речь в гл. 6) либо разделить алгоритм на две части. Рассмотрим последний способ. Для этого удалим из алгоритма несколько связанных по смыслу икон, а вместо них нарисуем икону-заместитель, которая называется вставкой (рис. 29б). Вставка нужна, чтобы напомнить об изъятых иконах. Вставка занимает мало места — намного меньше, чем выброшенные иконы, поэтому алгоритм становится короче. Разумеется, выброшенные иконы не пропадают — они образуют новый алгоритм — алгоритм-вставку.
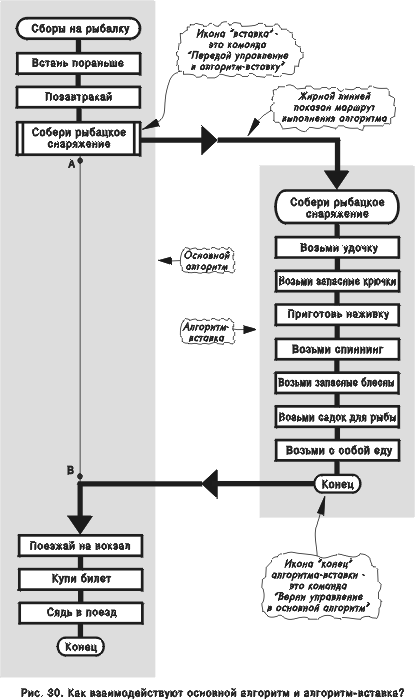
Икона-вставка — это команда “Передай управление в алгоритм-вставку” (рис. 30). Икона “конец” алгоритма-вставки означает: “Верни управление в основной алгоритм”. При этом управление возвращается в точку, расположенную после иконы-вставки. На языке программистов алгоритм-вставка — это процедура, а икона-вставка — это оператор “Вызов процедуры”.
ЧТО ТАКОЕ ПОДСТАНОВКА?
Операция “подстановка” связана с использованием иконы-вставки. Она выполняется за три шага.
Шаг 1. Из дракон-схемы удаляется фрагмент, имеющий один вход и один выход.
Шаг 2. Вместо него подставляется икона-вставка с именем Х.
Шаг 3. К удаленному фрагменту добавляется икона-заголовок с тем же именем Х и икона-конец; в результате получается алгоритм-вставка.
Два алгоритма на рис. 29 неравносильны: их формулы не совпадают, поскольку маршрут на рис. 29а содержит 14 икон, а на рис. 29б — 17 икон (см. также рис. 30). Вместе с тем нетрудно убедиться, что подстановка — эквивалентное преобразование алгоритмов, так как исходный и преобразованный алгоритмы дают одинаковые результаты для одних и тех же исходных данных. Попутно заметим, что равносильные алгоритмы всегда эквивалентны (обратное неверно). Таким образом, операция “подстановка” представляет собой эквивалентное (но не равносильное) преобразование алгоритмов.
|
 рис. 29
рис. 29
|

рис. 30
|
 Рис. 31 — на 2 стр.
Рис. 31 — на 2 стр.


УЛУЧШЕНИЕ ЭРГОНОМИЧНОСТИ АЛГОРИТМОВ
С ПОМОЩЬЮ ЦЕПОЧКИ
ЭКВИВАЛЕНТНЫХ ПРЕОБРАЗОВАНИЙ
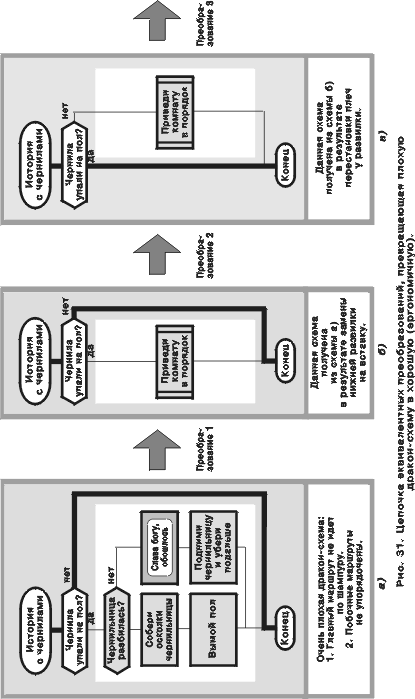
Когда рисуешь алгоритм, нужно стремиться, чтобы он с самого начала удовлетворял правилам и был эргономичным. А если это не получилось? Если первый блин комом, как на рис. 31а? В этом случае необходимо довести алгоритм до ума с помощью последовательности эквивалентных преобразований. Вообще говоря, в примере на рис. 31а достаточно сделать всего две рокировки (преобразовав обе развилки)
и мы сразу получим нужный ответ — искомую эргономичную схему на рис. 31д.
Однако, чтобы сделать изложение более наглядным, лучше избрать другой путь и двигаться к цели мелкими шажками. Для начала используем визуальную формулу на рис. 32 и с ее помощью заменим нижнюю развилку на рис. 31а на икону-вставку “Приведи комнату в порядок”. Результат подстановки представлен на рис. 31б. Затем выполним рокировку и получим схему на рис. 31в. После этого произведем обратную подстановку по формуле на рис. 32 и заменим икону-вставку на развилку “Чернильница разбилась?” Полученная схема показана на рис. 31г. Наконец, делаем еще одну рокировку и приходим к искомой эргономичной схеме на рис. 31д.
|
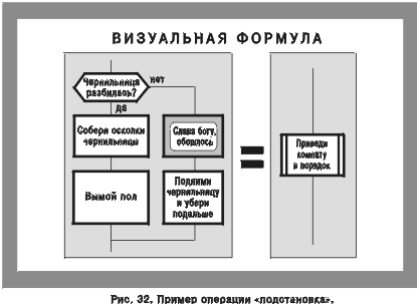
Для удобства читателя на рис. 33 дана общая сводка эквивалентных преобразований.
ВЫВОДЫ
1. Понятие эргономичного алгоритма весьма актуально. Применение достижений эргономики к теории алгоритмов позволяет значительно улучшить понимаемость алгоритмов и программ.
2. Понятие эргономичного алгоритма задается с помощью конечного набора четко определенных правил и признаков, таких, как “главный маршрут должен идти по шампуру” и т. д. Следовательно, это понятие является строгим.

3. Рассмотренные выше четыре эквивалентных преобразования алгоритмов подтверждают, что эргономичность алгоритмов можно улучшить с помощью простых и ясных методов, которые в некотором смысле можно считать формальными.
Г Л А В А 8
Визуализация циклов
Успешность принятия решения во многом зависит от способности человека “визуализировать проблемную ситуацию”, наглядно представлять ее и оперировать наглядными образами.
Наталья Завалова, Борис Ломов,
Владимир Пономаренко
ОБЫЧНЫЙ ЦИКЛ
В языке ДРАКОН имеется следующий ассортимент циклов:
! обычный цикл;
! переключающий цикл;
! цикл ДЛЯ;
! веточный цикл;
! цикл ЖДАТЬ.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
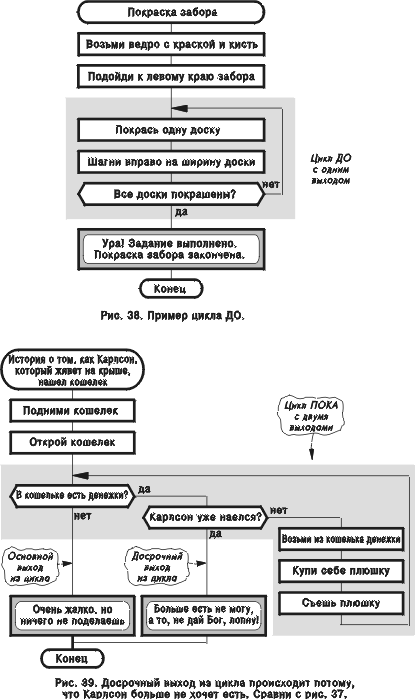
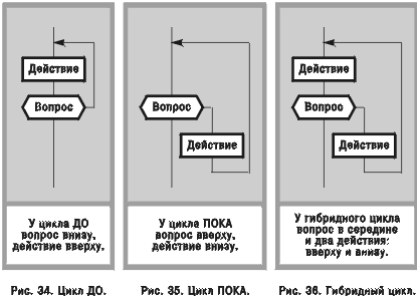
Составной визуальный оператор “обычный цикл” (рис. 2, макроикона 4) содержит иконы “вопрос” и “петля цикла” (рис. 1, иконы И4, И24). Он охватывает циклы трех типов (рис. 34—36):
! цикл ДО (do-while),
! цикл ПОКА (while-do),
! гибридный цикл (do-while-do).
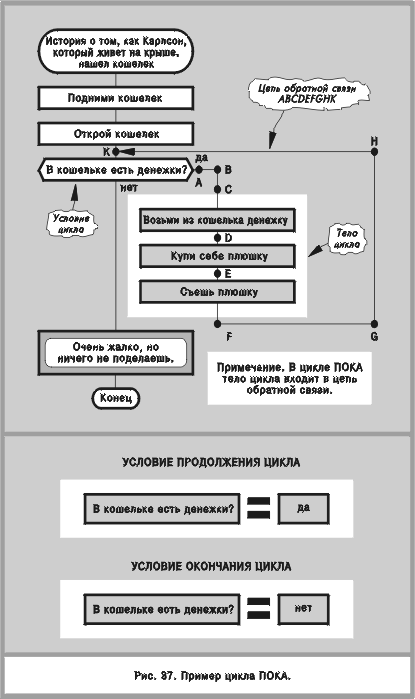
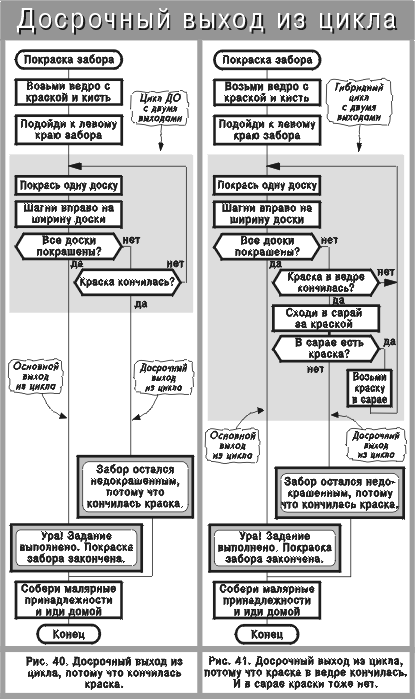
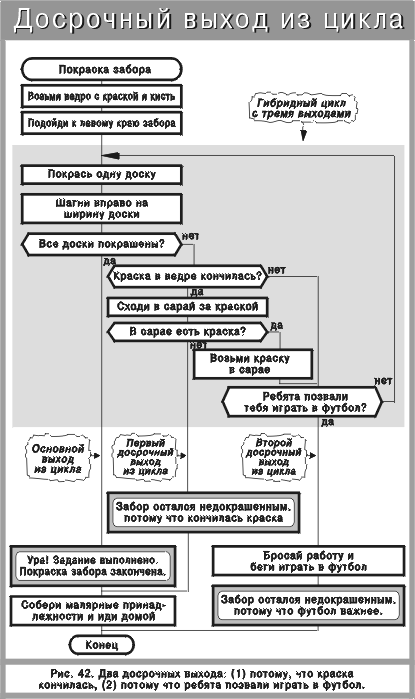
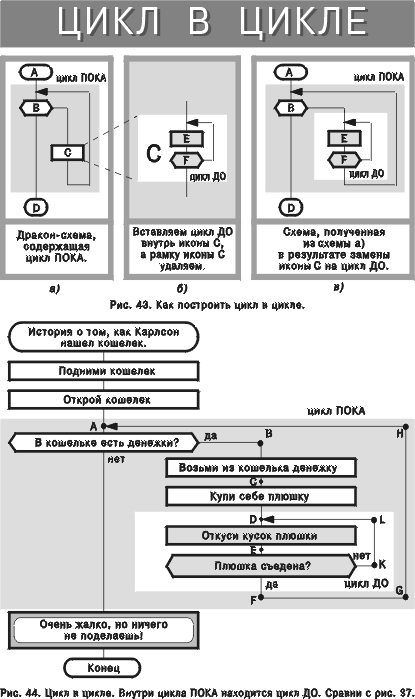
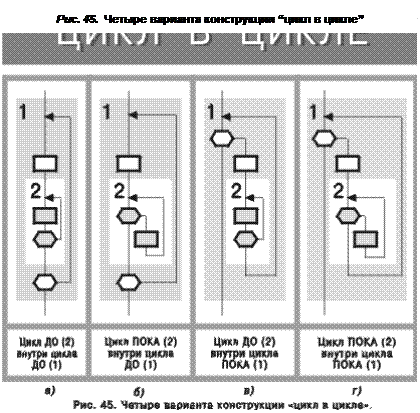
Примеры циклов ПОКА и ДО приведены на рис. 37, 38. Досрочный выход из цикла показан на рис. 39—42. Конструкция “цикл в цикле” представлена на рис. 43—45.
Анализируя рисунки, можно заметить следующие особенности.
! Оператор “обычный цикл” имеет один вход и один или несколько выходов.
! Цикл с одним выходом представляет собой шампур-блок (вход и выход находятся на одной вертикали).
! Если цикл имеет более одного выхода, основной выход размещается на главной вертикали, дополнительные — правее ее.
! Петля цикла находится правее главной вертикали и закручена против часовой стрелки.
! Икона “вопрос” задает условие цикла, которое распадается на две части: условие продолжения и условие окончания (рис. 37).
! Условие продолжения соответствует правому выходу иконы “вопрос”, условие окончания — нижнему.
! Условие окончания может помечаться как словом “нет”, так и словом “да”. То же самое относится и к условию продолжения.
ПЕРЕКЛЮЧАТЕЛЬ И ПЕРЕКЛЮЧАЮЩИЙ ЦИКЛ
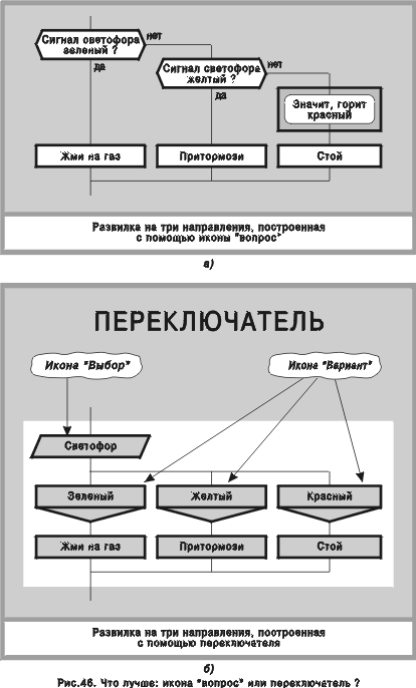
Предположим, в алгоритме нужно организовать разветвление на несколько направлений. Задачу можно решить двумя способами: с
помощью иконы “вопрос” (рис. 46а) и с помощью переключателя (рис. 46б).
Переключатель — составной визуальный оператор (рис. 2, макроикона 3), имеющий один вход и один выход, содержащий одну икону “выбор” и несколько (две и более) икон “вариант” (рис. 1, иконы И5, И6). Внутри иконы “выбор” делается надпись, обычно в утвердительной форме, которая обозначает вопрос, имеющий строго определенное число ответов (два и более). Ответы записываются в иконах “вариант”. Таким образом, число вариантов равно числу ответов. Говоря формально, в иконе “выбор” записывается переменная, в иконах “вариант” — ее значения. На рис. 46б переменная “Светофор” принимает три значения: зеленый, желтый, красный.
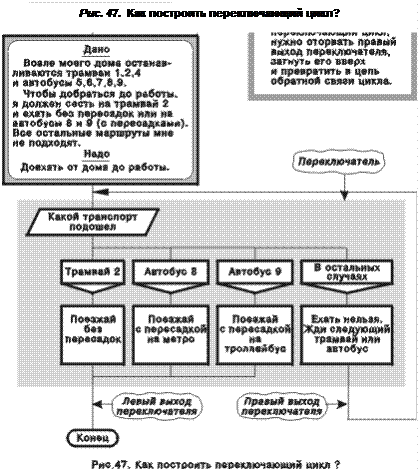
Переключатель позволяет создать особый тип цикла — переключающий цикл (рис. 2, макроикона 5). Для этого нужно оторвать выход правой ветви переключателя, загнуть его вверх и присоединить стрелку в нужное место (рис. 47).
На рис. 48 изображен цикл с переключателем, однако это не переключающий цикл, а обычный. Как их отличить? В первом случае переключатель имеет два выхода, во втором — только один. Есть еще одно отличие. Если вверх загибается выход иконы “вопрос” — это обычный цикл (ДО, ПОКА или гибридный). А если кверху идет выход переключателя — перед нами переключающий цикл.
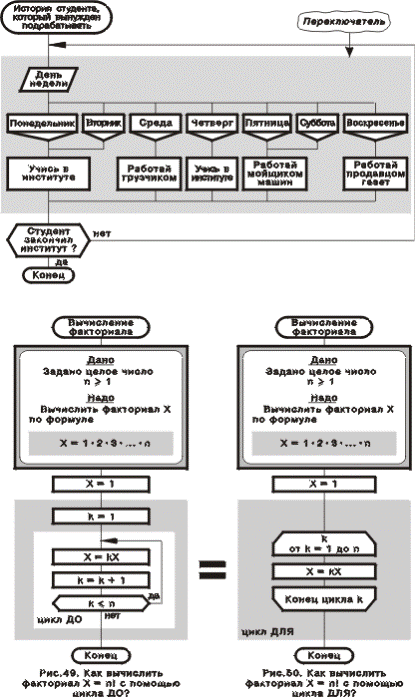
ЦИКЛ ДЛЯ
На рис. 49 и 50 показаны два варианта решения простой математической задачи. В первом случае используется цикл ДО, во втором — цикл ДЛЯ. Цикл ДЛЯ — составной визуальный оператор (рис. 2, макроикона 6), содержащий иконы “начало цикла ДЛЯ” и “конец цикла ДЛЯ” (рис. 1, иконы И12, И13), между которыми располагаются одна или несколько других икон. Внутри иконы “начало цикла ДЛЯ” указываются переменная цикла, ее начальное и конечное значения и шаг. Порядок
|
|
записи этих величин определяется выбранным вариантом текстового синтаксиса. На рис. 50 изображен вариант, по умолчанию принимающий, что шаг равен 1.
ВЕТОЧНЫЙ ЦИКЛ
Циклы, описанные выше, могут использоваться как в примитиве, так и в силуэте. В этом параграфе речь пойдет о веточном цикле, который встречается только в силуэте.
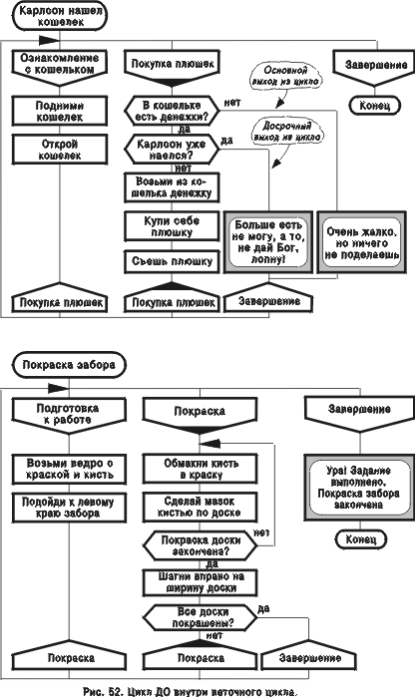
Веточный цикл образуется, когда метка в иконе “адрес” указывает либо на свою ветку, либо на ветку, которая находится левее. Например, икона-адрес “Покупка плюшек” на рис. 51 указывает на свою ветку. Внутри веточного цикла могут появляться циклы других типов. На рис. 52 изображена конструкция “цикл в цикле”, у которой внутри веточного цикла находится цикл ДО.
|

рис.48, 49, 50
|

51, 52
|
 53
53
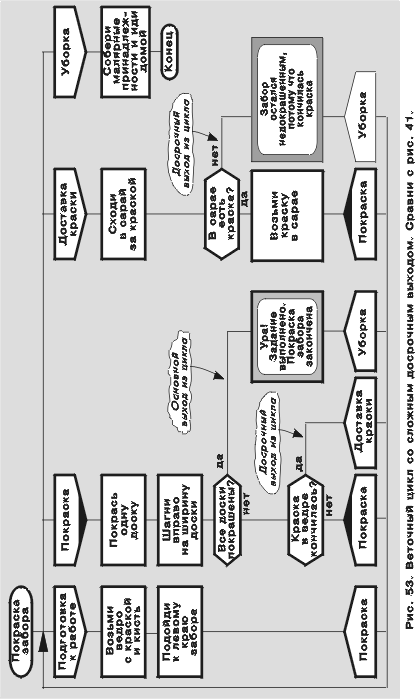
При замене примитива на эквивалентный ему силуэт гибридный цикл нередко превращается в веточный цикл. В этом легко убедиться, сравнив эквивалентные алгоритмы на рис. 41 и 53.
ГЛАВНЫЙ МАРШРУТ СИЛУЭТА
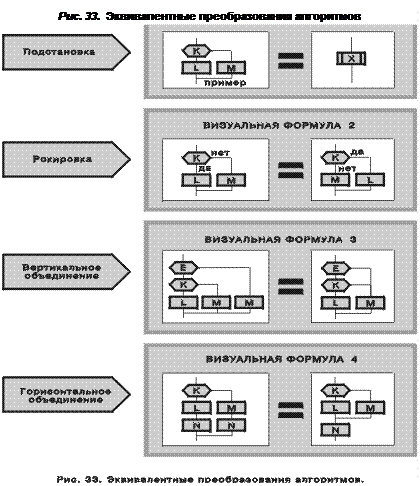
В этом параграфе мы продолжим изучение веточных циклов и попытаемся ответить на вопрос: как найти главный маршрут веточного цикла? Для этого нужно проанализировать понятие “главный маршрут силуэта” (рис. 54).
Линейный (неразветвленный) силуэт имеет один-единственный маршрут, который и является главным. Он проходит по шампурам всех веток и по всем иконам силуэта (рис. 54а).
 |
Формула маршрута для силуэта имеет особенность: одноименные иконы “адрес” и “имя ветки” обозначаются одной буквой, которая повторяется в формуле дважды. Например, силуэт на рис. 54а имеет формулу
где парные буквы обозначают переход с первой ветки на вторую (С — С) и со второй на третью (D — D).
Ветка называется одноадресной, если она имеет одну икону “адрес”. Если все ветки одноадресные, силуэт считается одноадресным.
Линейный силуэт всегда одноадресный. Однако одноадресный силуэт может быть и разветвленным. В последнем случае его главный маршрут следует по шампурам всех веток, однако он не проходит по всем иконам (рис. 54б).
Если хотя бы одна ветка имеет более одного адреса, может сложиться ситуация, когда какие-то ветки не попадают на главный маршрут. На рис. 54в икона-адрес D лежит на побочном маршруте. Это приводит к тому, что ветка D также оказывается на побочном маршруте. В результате главный маршрут проходит по шампурам всех веток, кроме ветки D (рис. 54в).
Веточные циклы образуются только в многоадресных силуэтах, в одноадресных их в принципе не может быть. Они бывают нескольких типов:
! одноветочные (если цикл помещается в одной ветке);
! двухветочные (если цикл занимает две ветки);
! трехветочные (цикл в трех ветках)
и т. д.
 |
Как работает одноветочный цикл? Предположим, до начала выполнения цикла на рис. 54г имеют место условия
|

54

Предположим также, что веточный цикл выполняется два раза, после чего условие Е принимает значение “нет”. Это значит, что при третьем проходе по ветке В произойдет выход из цикла по пути “Е нет С”. В такой ситуации формула главного маршрута для силуэта на рис. 54г принимает вид:
Как выглядит главный маршрут на дракон-схеме? Ответ изображен жирной линией на рис. 54г. Мы видим, что главный маршрут как бы разветвляется в иконе Е и проходит через оба ее выхода. Разумеется, это условность, которая означает следующее. Сначала (когда Е = да) главный маршрут идет по шампуру, затем (когда выполняется условие окончания цикла Е = нет) главный маршрут проходит через правый выход иконы Е.
Чтобы построить одноветочный цикл, нужно в левой иконе “адрес” записать Х, где Х — имя данной ветки. Для выхода из цикла следует добавить вторую икону “адрес” и записать в ней Y, где Y — имя следующей (по порядку исполнения) ветки.
Если в веточном цикле слишком много икон, он может не поместиться в одной ветке. К счастью, его можно разделить на части. Например, веточный цикл на рис. 54д содержит пять икон: Е, F, G, H, R (иконы “имя ветки” и “адрес” не в счет). Поместим иконы Е и F в ветку В,
а иконы G, H, R — в ветку С. В результате цикл станет двухветочным. Главный маршрут силуэта с двухветочным циклом имеет разветвление в иконе R. Условие R = да позволяет вернуться к началу цикла. Если
R = нет, главный маршрут ведет нас к концу алгоритма (рис. 54д).
Таким образом, двухветочный цикл — это цикл, содержащий две ветки Х и Y, причем в ветке Х имеется икона-адрес Y, а в ветке Y — икона-адрес Х.
На рис. 54е представлена ситуация “цикл в цикле”: веточный цикл С находится внутри веточного цикла В. Из рисунка видно, что в этом случае главный маршрут “разветвляется” дважды: в иконах R и J.
 |
Если выполняется условие R = да, происходит повторение внутреннего цикла С. При сочетании условий
производится выход из цикла С и повторение внешнего цикла В. Наконец, сочетание условий

означает, что выполнение цикла В и алгоритма в целом заканчивается.
ВЫВОДЫ
1. В различных текстовых языках при описании циклов применяются разные наборы ключевых слов, имеющих к тому же разную семантику. Неразбериху усугубляют отличия в логике окончания цикла. Например, в языке Си для циклов while и do-while условие окончания цикла соответствует значению false или 0, условие продолжения — значению true или 1. В языке Паскаль картина иная: в цикле while-do выход из цикла соответствует значению false, а в цикле repeat-until по каким-то загадочным причинам применяется диаметрально противоположный принцип: выход из цикла производится, когда логическое выражение принимает значение true. Все эти путаные правила программист обязан знать и неукоснительно выполнять.
2. Отсутствие унификации ключевых слов и разнобой в определении условий выхода из цикла является серьезным недостатком: программисты вынуждены зубрить ключевые слова и значения условий, причем освоение каждого следующего языка требует новой зубрежки.
3. С точки зрения визуального программирования, указанные трудности являются надуманными и легко устраняются. Надо лишь отказаться от сложившихся привычек и устаревших стереотипов мышления, связанных с текстовым программированием. Визуализация качественно меняет ситуацию, поскольку текст больше не является единственным носителем информации.
4. Визуальные образы уменьшают нагрузку на память программиста, ликвидируют ошибки, вызванные неправильным пониманием семантики ключевых слов, отменяют ненужные ограничения, предоставляют пользователю богатую палитру выразительных средств и в конечном итоге обеспечивают более высокую понимаемость алгоритмов и программ.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|