Исходные данные. Задача 1

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра «Электропривода и автоматизации промышленных установок»

РАСЧЁТНО-ГРАФИЧСКАЯ РАБОТА

по предмету:ТЕОРИЯ СПЕЦИАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ

ВариаНТ 26

Выполнил:

Студент группы ЭМА-72

Журавлев Алексей Аркадьевич

Проверила:

к.т.н., доц. Кучер Екатерина Сергеевна

Новосибирск 2020г.

Исходные данные

Таблица 1 — Параметров объекта управления


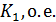
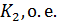
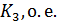
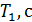
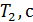
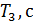
2.2	1.5	2.0

Структурная схема №2 объекта управления изображена на рисунке 1:

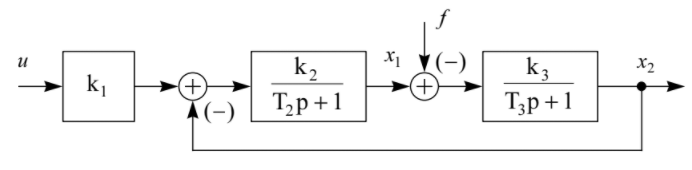
Рисунок 1 — Структурная схема объекта управления

Задача 1

Представить математическую модель объекта управления, заданную структурной схемой, в векторно-матричной форме. Определить установившиеся значения координат состояния объекта при подаче единичных управляющего и возмущающего воздействий.

Решение:

Представим математическое описание объекта управления, заданное структурной схемой, в виде операторных уравнений:

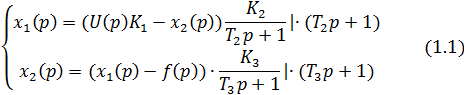
Перейдём к дифференциальной форме записи:

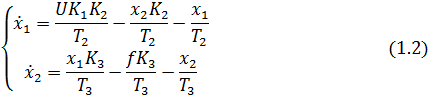
Векторно-матричную модель заданного объекта представляется в форме [1. cт.13]:

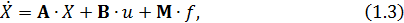
где 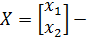двумерный вектор координат состояния; 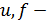скалярные управляющие и возмущающие воздействия соответственно; 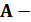собственная матрица объекта управления:

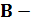матрица управлений:

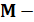матрица возмущений, характеризующая вхождение сигнального возмущающего воздействия 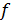в структуру объекта управления :

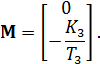
Определим установившиеся значения координат состояния объекта управления при подаче управляющего и возмущающего воздействий путём векторно-матричных преобразований^[1]. Модель (1.3) с использованием оператора Лапласа примет вид:

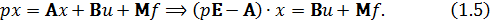
Из уравнения 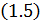выражаем :

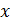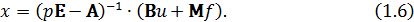
Разделив левую и правую части уравнения (1.6) на u, при 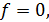получим матричную передаточную функцию ОУ по управлению^[1]:

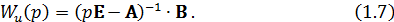
Аналогично при 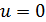получаем матричную передаточную функцию ОУ по возмущению:

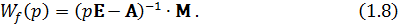
Установившиеся значения координат состояния объекта при подаче единичного управляющего воздействия найдём на основании уравнения (1.7) при 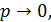принимая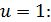

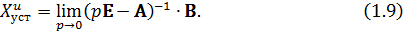
По аналогии определяются установившиеся значения объекта управления при подаче единичного возмущающего воздействия ( ):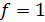

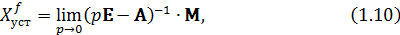
где 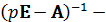обратная матрица, которая определяется выражением:

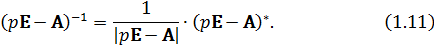
Найдём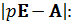

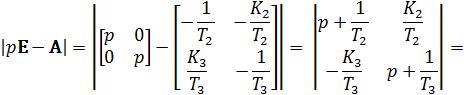
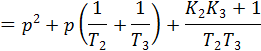
Подставляя значения всех параметров, получаем:

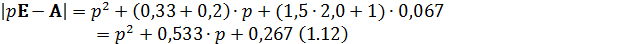
Получим присоединённую матрицу 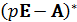из исходной путём замены всех элементов их алгебраическими дополнениями с последующим транспонированием^[1]:

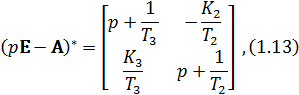
тогда

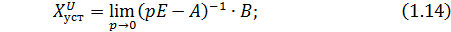
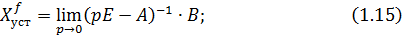
С учётом уравнени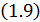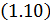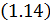й , , и 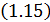установившиеся значения координат состояния при подаче единичного сигнала управления:

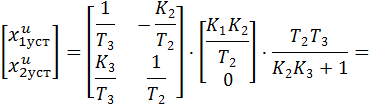
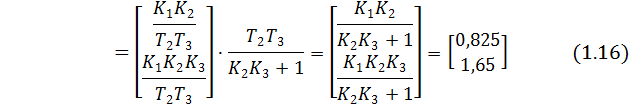
при подаче единичного сигнала возмущения:

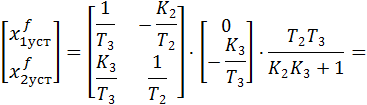
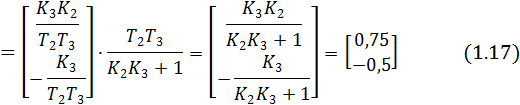
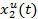
Проверка результатов расчетаматематической модели:

t,c

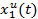
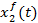
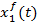
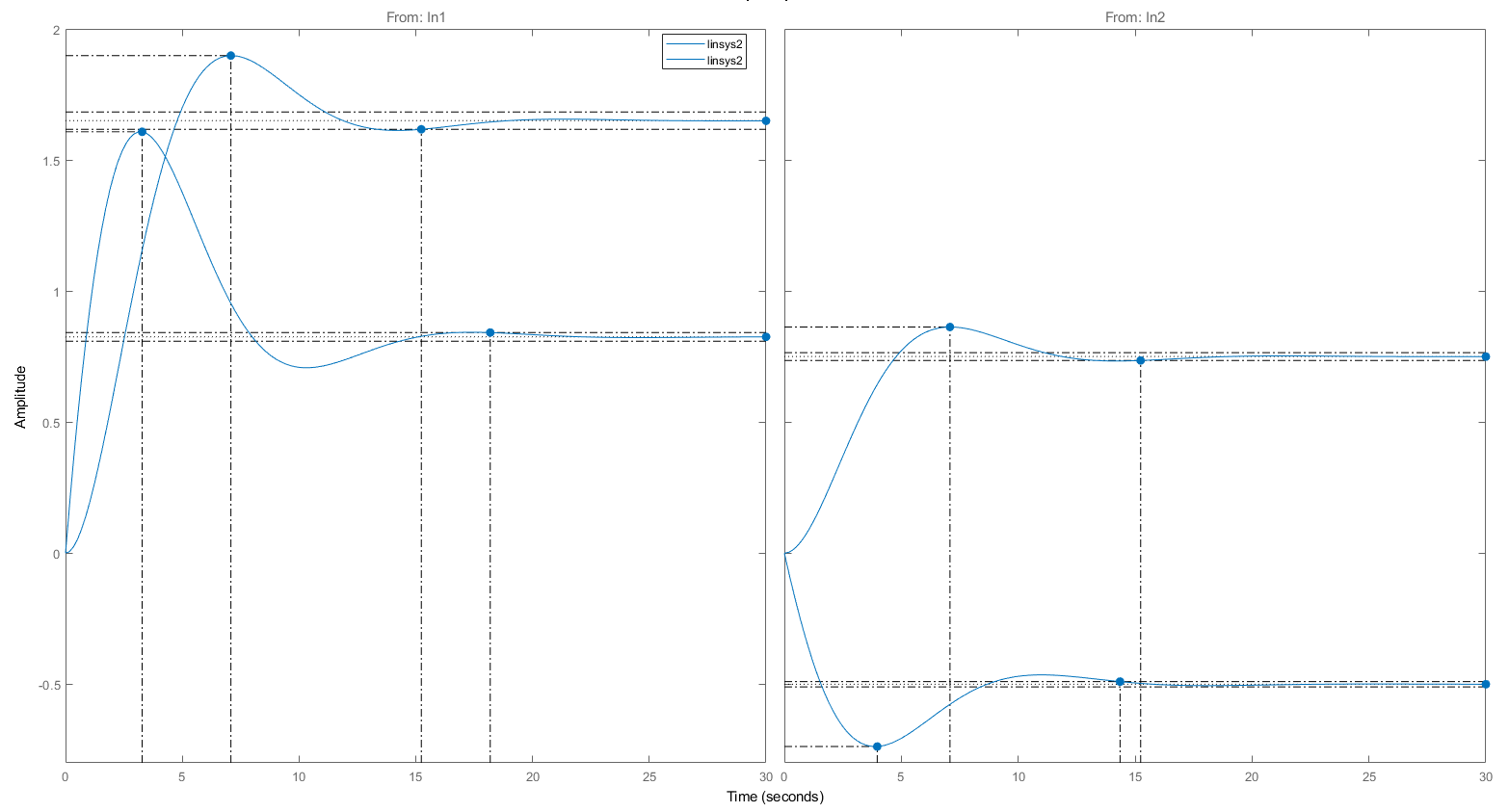
Рисунок 2 — Графики переходных процессов координат состояния объекта управления по управляющему и возмущающему воздействиям

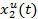
t,c

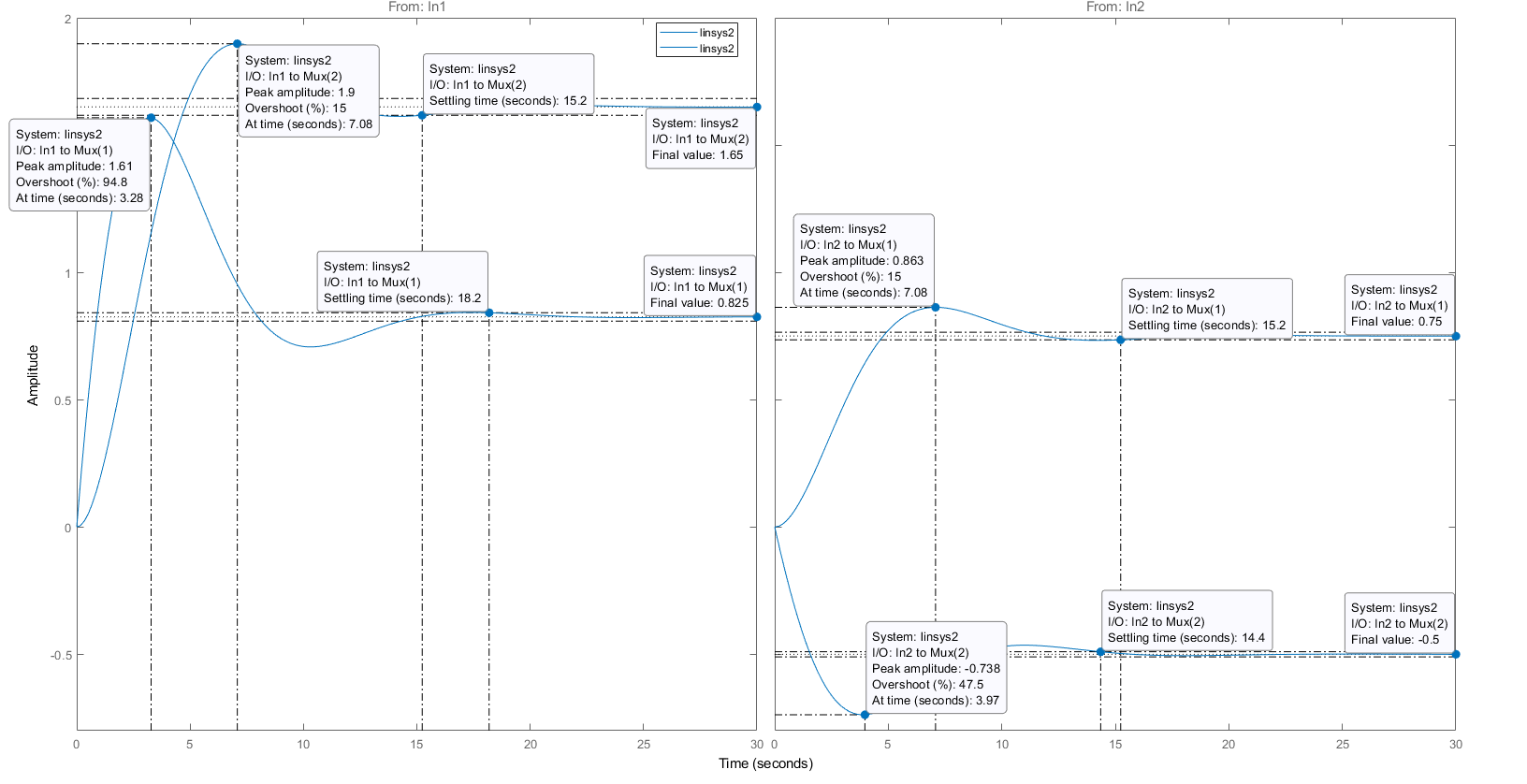
Рисунок 3 — Показатели качества объекта управления

Определим прямые показатели качества переходного процесса объекта управления и установившиеся значения 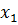и 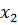, результаты сведены в таблицу 2.

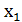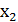Таблица 2 – Прямые показатели качества переходного процесса объекта управления и установившиеся значения координат и при единичном возмущащем и управляющем воздействиях

Показатель	Управляющее воздействие		Возмущающее воздействие
Показатель
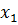
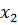
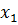
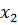
Перерегулирование, %	94,8			47,5
Время регулирования, сек	18,2	15,2	15,2	14,4
Количество колебаний, шт
Установившиеся значение, о.е.	0,825	1,65	0,75	-0,5

Вывод:

В результате моделирования были получены переходные характеристики координат состояния объекта управления по управляющему и возмущающему воздействиям (Рис.3). Установившиеся значения координат состояния объекта управления, полученные по переходным характеристикам, были проверены аналитически. В следствии проверки можно увидеть, что рассчитанные и смоделированные значения координат состояния объекта управления полностью совпадают. В соответствии с этим можно говорить о правильности расчета.

Задача 2

Синтезировать алгоритм модального управления заданным объектом при полных измерениях и настройке системы на желаемое распределение корней характеристического полинома, соответствующее стандартной линейной форме Бесселя. Среднегеометрический корень характеристического полинома принять равным [1, ст. 63]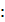

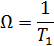
Решение:

Перед началом синтеза модального регулятора необходимо произвести проверку условия управляемости. Для заданного объекта матрица управляемости Yимеет вид [1, ст. 44]:

Определим матрицу AB:

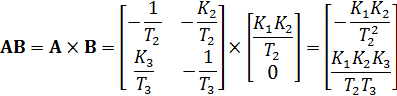
Тогда:

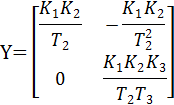
Определитель матрицы Yравен:

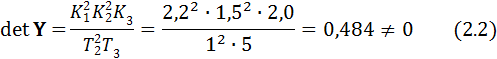
Из последнего неравенства видно, что ранг матрицы управляемости Yравен порядку объекта управления:

т.е. объект является полностью управляемым.

В задачу синтеза закона модального управления входит нахождение коэффициентов передачи каналов отрицательных обратных связей по координатам состояния 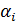, преднамеренное введение в систему которых обеспечивает желаемое распределение корней характеристического уравнения замкнутой системы.

Скалярное управляющее воздействие uформируется на основании следующего закона управления [1, ст. 50]:

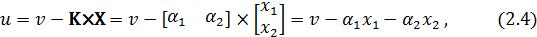
где 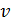– скалярное задающее воздействие.

Структурная схема синтезированной системы модального управления (СМУ) изображена на рисунке 2:

α₁

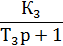
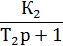
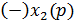
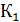
α₂

Рисунок 4 — Структурная схема объекта управления с модальным корректором

Подстановкаалгоритма (2.4) в математическую модель (1.3) изменяет её вид:

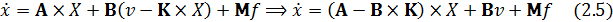
Переходя к операторной форме, имеем:

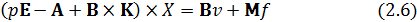
В результате собственные динамические свойства замкнутой системы модального управления теперь описываются определителем 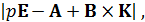который является её характеристическим полиномом:

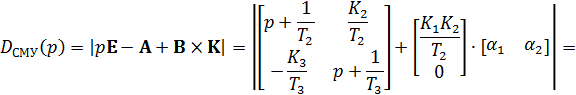
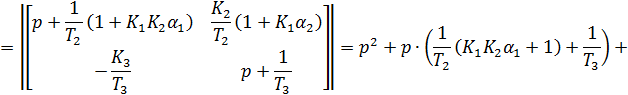
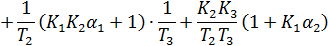
Подставляя значения всех параметров, получаем:

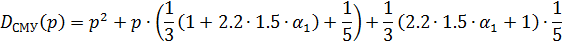
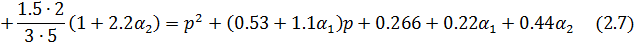
Приравнивая полученный характеристический полином к стандартному виду:

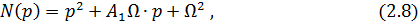
получаем систему алгебраических уравнений:

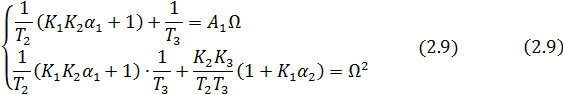
из которой найдем элементы матрицы 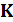, выбирая среднегеометрический корень равным 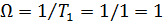, а также коэффициент формы 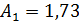. [1, табл. П1.4]

Из первого уравнения системы (2.9)

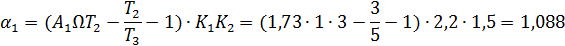
Согласно второму уравнению системы (2,9):

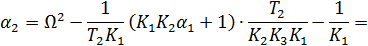
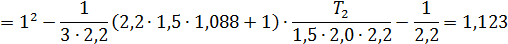
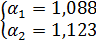
Установившиеся значения координат состояния при подаче единичных задающего и возмущающего воздействий определяются по формулам^[1]:

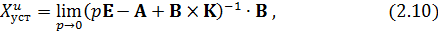
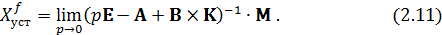
Получим присоединённую матрицу 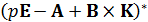из исходной путём замены всех элементов их алгебраическими дополнениями с последующим транспонированием:

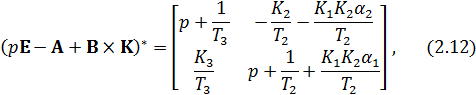
тогда:

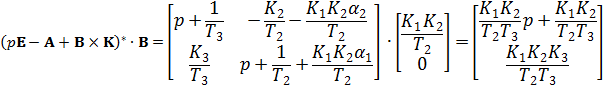
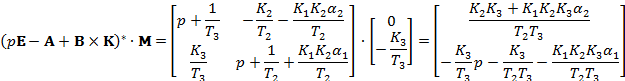
С учётом уравнений (2.10) и (2.11) и последних соотношении установившиеся значения координат состояния при подаче единичного сигнала управления:

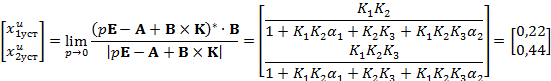
при подаче единичного сигнала возмущения:

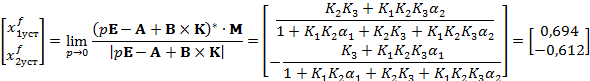
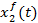
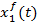
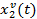
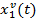
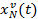
t,c

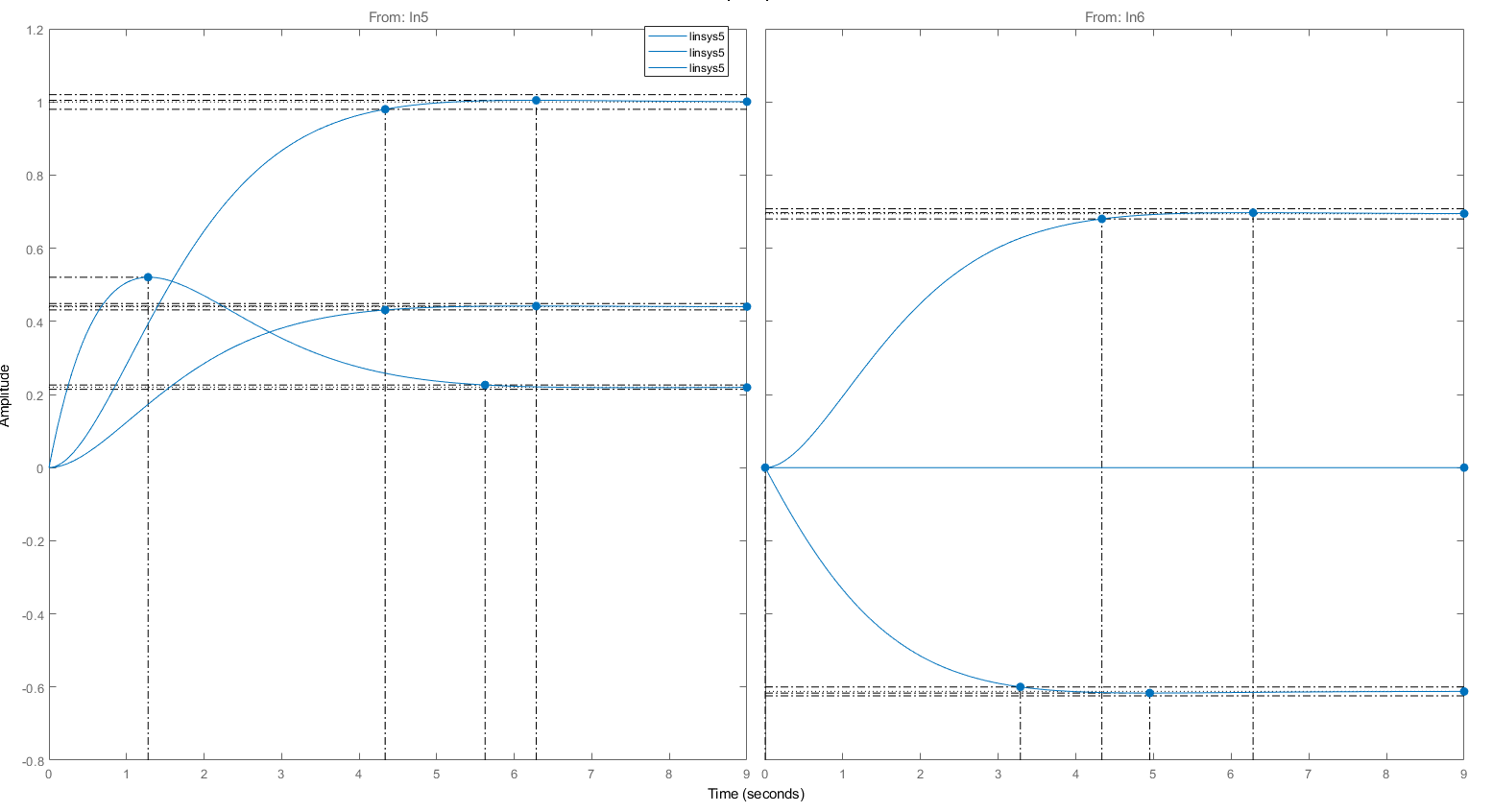
Рисунок 5 — Переходный процес системы с модальным регулятором при единичном задающем воздействии

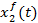
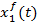
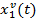
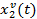
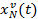
t,c

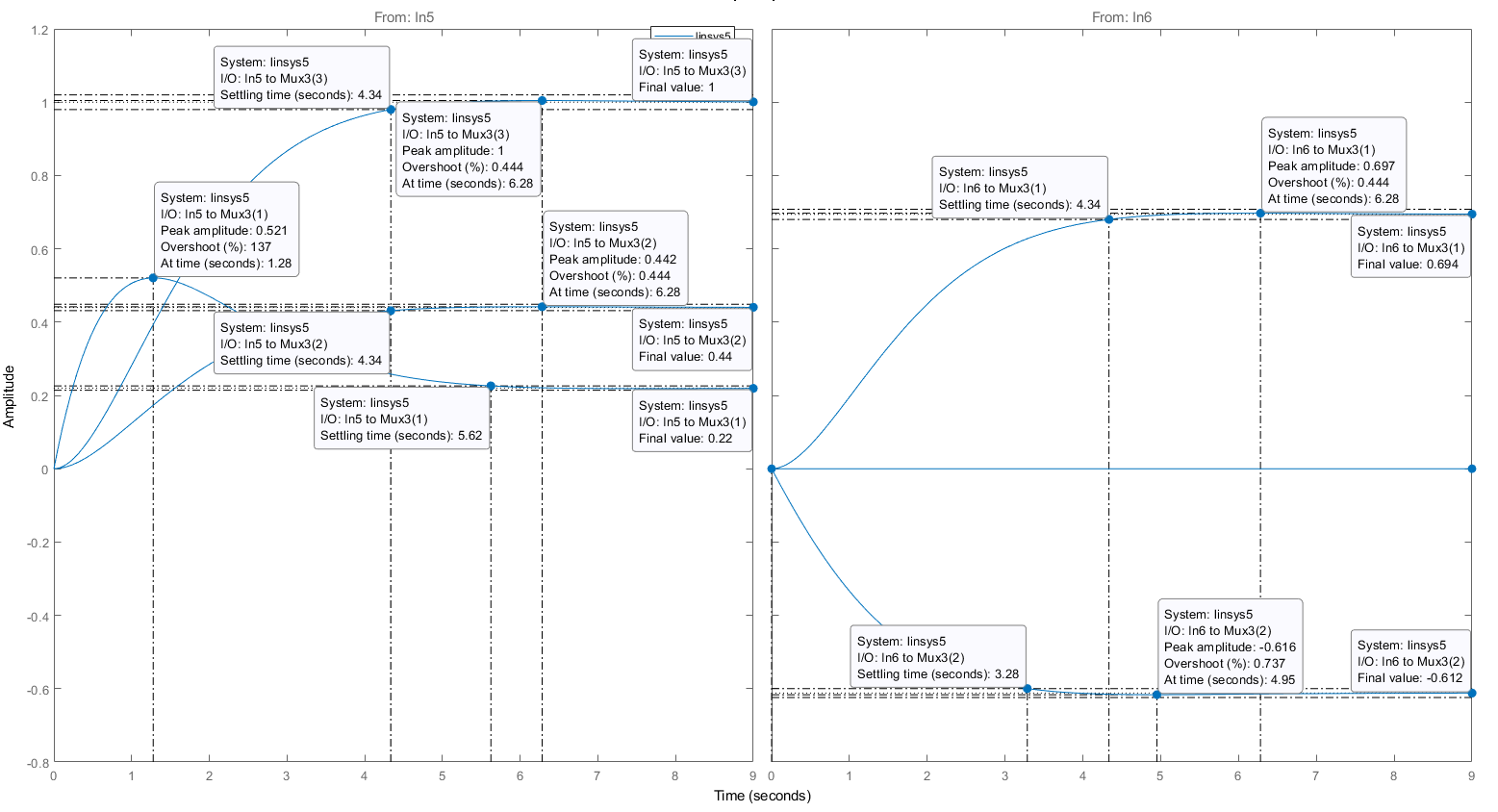
Рисунок 6 — Показатели качества системы с модальным регулятором при единичном управляющем и возмущающем воздействии

Определим прямые показатели качества переходного процесса системы с модальным регулятором и установившиеся значения 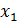и 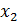, результаты сведены в таблицу 3.

Таблица 3 – Прямые показатели качества переходного процесса системы с модальным регулятором и установившиеся значения 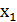и 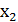при единичном возмущающем и управляющем воздействиях

Показатель	Управляющее воздействие		Возмущающее воздействие		Желаемый переходный процесс
Показатель
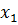
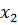
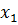
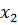
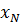
Перерегулирование, %		0,44	0,44	0,737	0,44
Время регулирования, сек	5,62	4,34	4,34	3,28	4,34
Количество колебаний, шт
Установившиеся значение, о.е.	0,22	0,44	0,694	-612

Рассчитаем погрешности настройки системы:

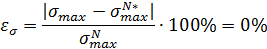
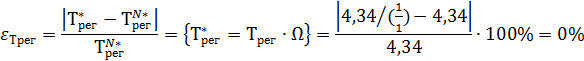
Вывод:

В ходе решения данной задачи был проведен синтез алгоритма модального управления заданным объектом при полных измерениях и настройке системы на желаемое распределение корней характеристического полинома, соответствующее стандартной линейной форме Бесселя. Рассчитаны установившиеся значения координат состояния при подаче единичных задающих и возмущающего воздействий. Сняты показатели качества СМУ, такие как величина перерегулирования равная 0,44% и время регулирования 4,34 с. для 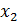, данные показатели качества имеют небольшую погрешность с желаемой САУ, что говорит о большой точности проведенных настроек, но в системе присутствует статическая ошибка.

Задача 3

Синтезировать наблюдатель Люенбергера полного порядка с распределением корней характеристического полинома, соответствующим стандартной линейной формеБесселя, и среднегеометрическим корнем, равным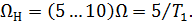

В качестве измеряемой координаты вектора состояния принять 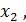возмущающее воздействие считать неконтролируемым.

Решение:

Динамическая подсистема для оценивания вектора координат состояния строится на основе математической модели объекта управления путём её дополнения «стабилизирующей добавкой» 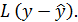Так как в системе производится прямое измерение 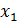, матрица выхода Сравна:

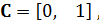
а сам вектор выходных переменных:

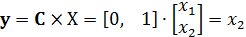
Полагая возмущающее воздействие неконтролируемым, на основании последних соотношений математическую модель наблюдателя Люенбергера полного порядка в пространстве состояний представим в следующем виде[1. ст.16]:

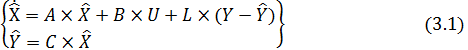
Или для системы второго порядка:

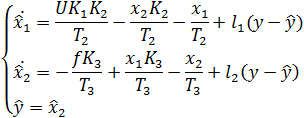
Синтез наблюдателя Люенбергера начинается с проверки условия наблюдаемости, выражаемого требованием равенства ранга матрицы наблюдаемости Нпорядку объекта управления. Матрица наблюдаемости для принятого объекта равна:

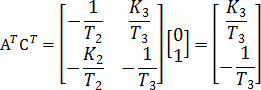
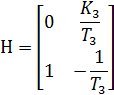
Определитель матрицы Нравен:

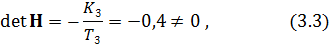
что удовлетворяет условию полной наблюдаемости:

Включение в подсистему оценивания координат «стабилизирующей добавки» влияет на собственные динамические свойства наблюдателя, которые должны обеспечивать требуемую форму и качество свободных составляющих переходного процесса в нём. По этой причине элементы матрицы Lопределяются путём приравнивания характеристического полинома наблюдателя полного порядка (НПП) [1. ст.17]:

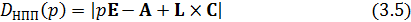
к нормированному полиному

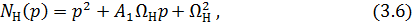
коэффициент формы, которого согласно условию задачи соответствует стандартной линейной форме 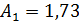и выбирается из таблицы. [1, табл. П1.4]

Увеличение среднегеометрического корня 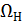по отношению к 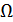позволяет разнести темпы процессов в синтезированной САУ с модальным регулятором и в подсистеме оценивания координат состояния, в результате чего наличие наблюдателя Люенбергера практически не оказывает влияния на динамику системы управления.^[1] Характеристический полином наблюдателя:

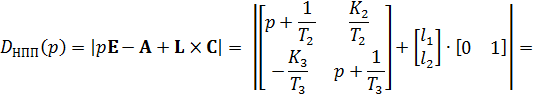
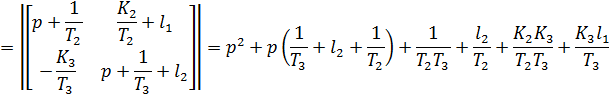
Приравнивая соответствующие коэффициенты из последнего уравнения и уравнения (3.6), получаем систему уравнений для вычисления компонентов матрицы L:

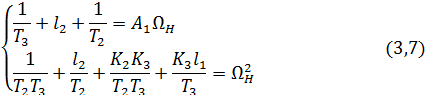
Выражаем 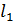и :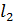

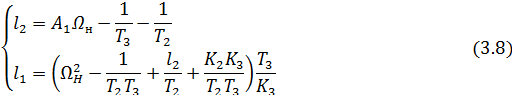
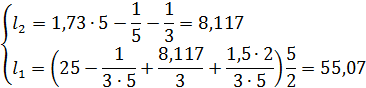
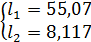
При дополнении системы модального управления динамической подсистемой оценивания координат состояния, по выходам которой замкнуты обратные связи, закон управления (2.4) преобразуется к виду^[1]:

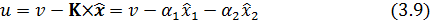
Структурная схема синтезированной замкнутой системы с наблюдателем Люенбергера полного порядка и модальным регулятором представлена на рисунке 7.

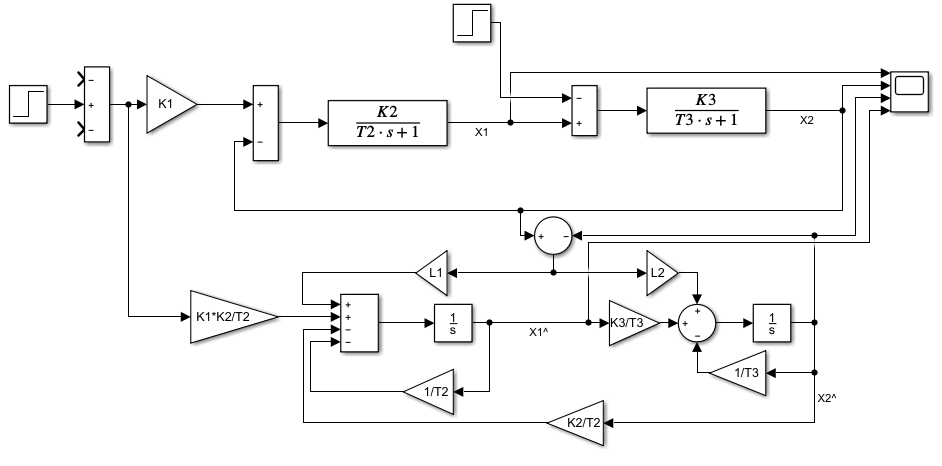
Рисунок 8 — Структурная схема замкнутой системы модального управления с наблюдателем полного порядка в программе MathLAB2019b

Xвых

t,c

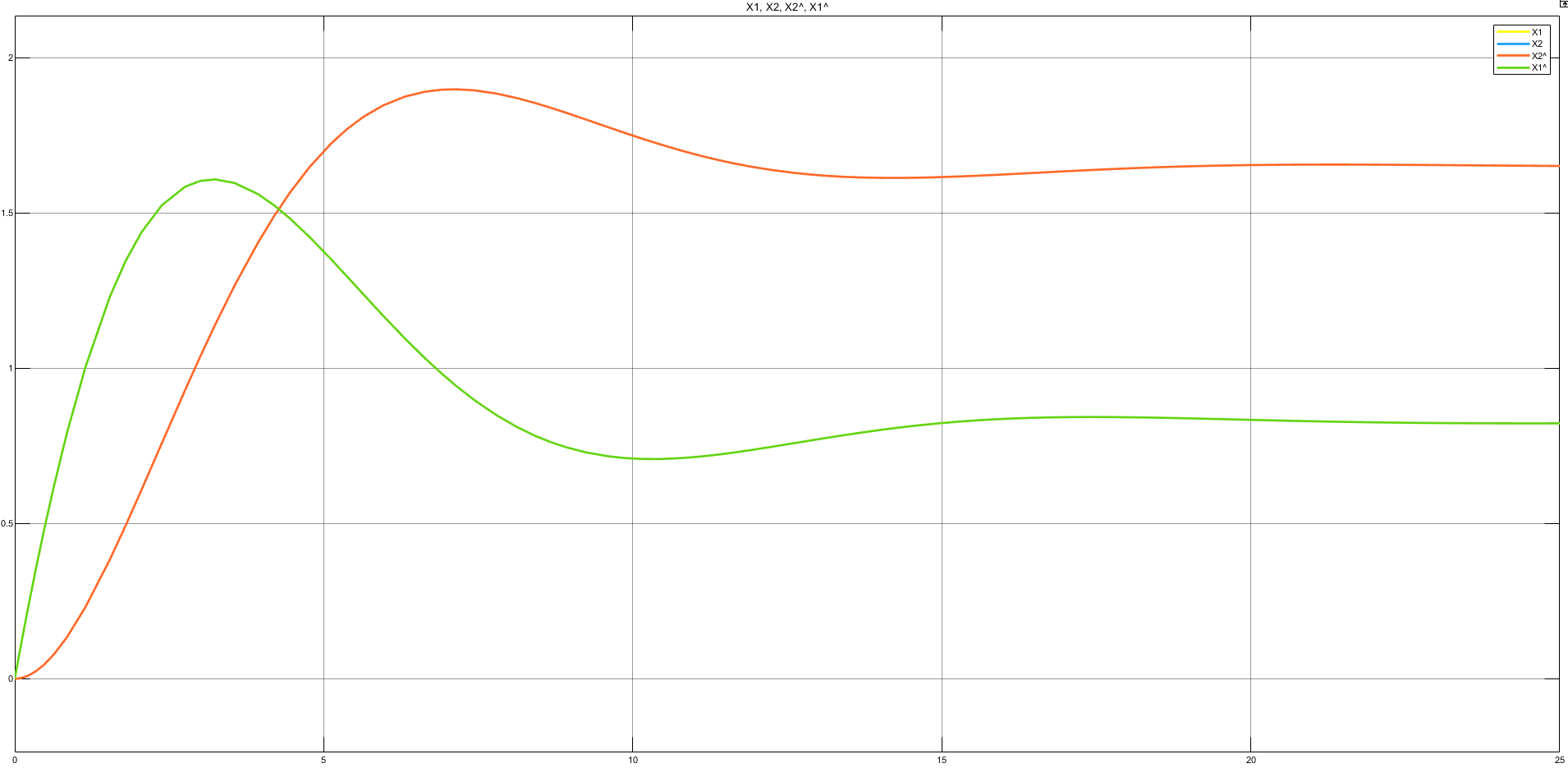
Рисунок 9 — Переходные характеристики координат состояния объекта управления и наблюдаемых координат состояния при нулевом возмущающем воздействии

Xвых

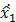
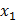
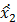
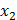
Вывод: графики переходных характеристик координат состояния объекта управления и оценок совпадают, следовательно, НПП структурно синтезирован, верно.

t,c

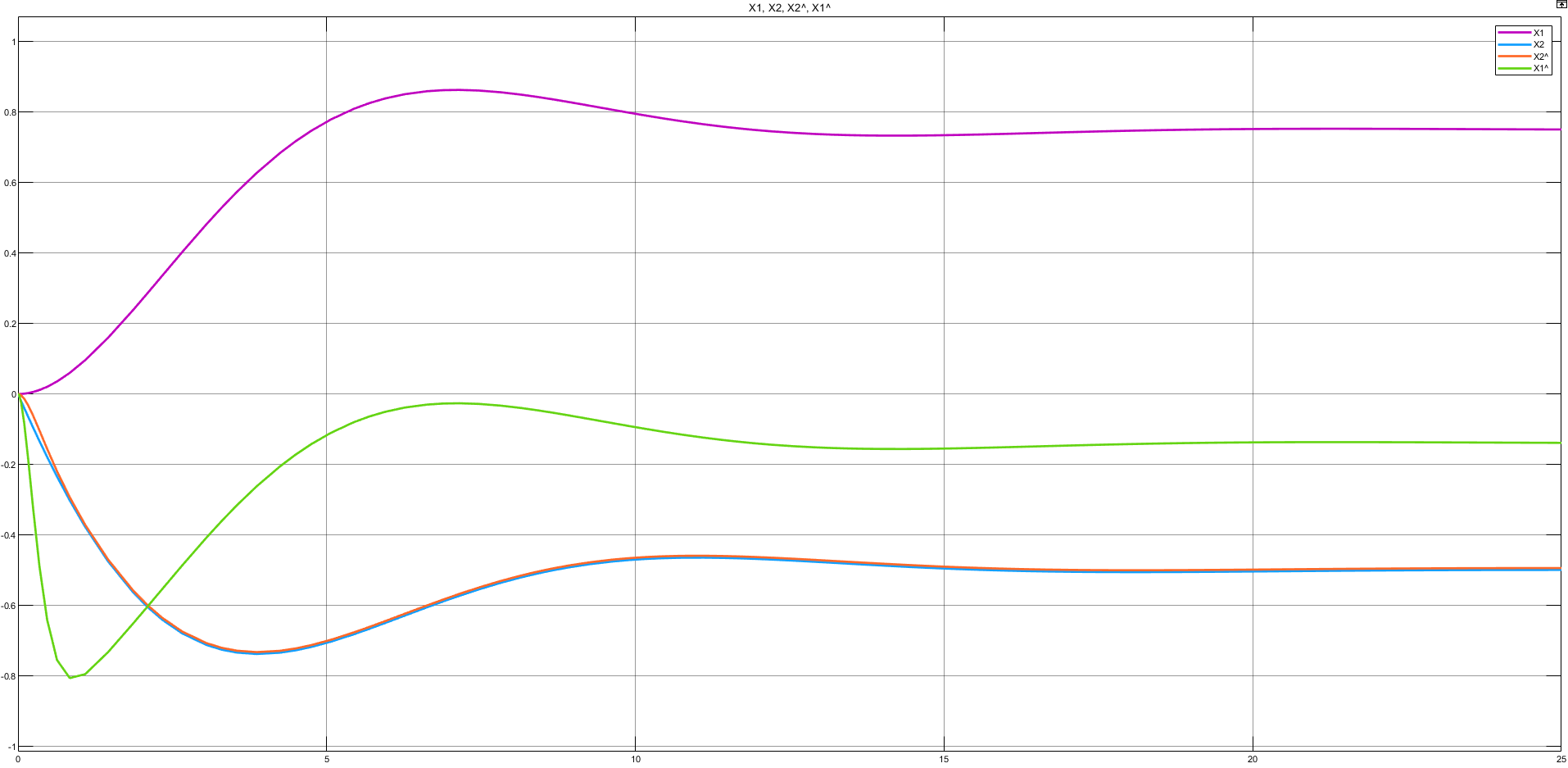
Рисунок 10 — Переходные характеристики координат состояния объекта управления и наблюдаемых координат состояния при нулевом управляющем воздействии

Рассчитаем статистическую ошибку наблюдения координат состояния 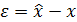объекта в наблюдателе полного порядка:

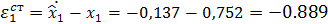
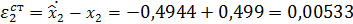
Вывод: при синтезе НПП возмущающее воздействие не учитывается, следовательно, возникает статическая ошибка регулирования в установившемся режиме

t,c

Xвых

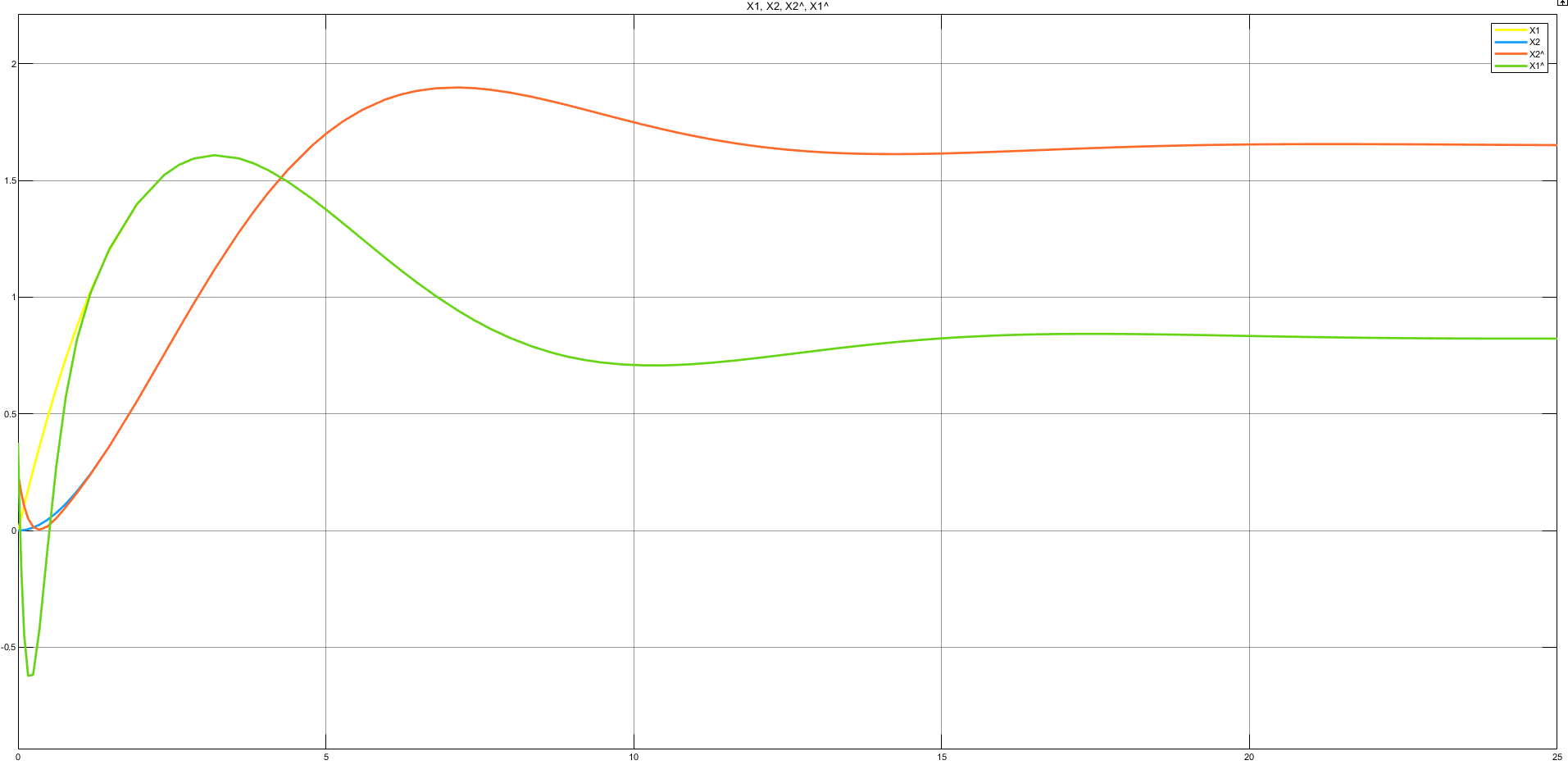
Рисунок 11 —— Переходные характеристики координат состояния объекта управления

и наблюдаемых координат состояния при нулевом возмущающем воздействии с начальными отклонениями

Xвых

Вывод: при отклонении от НУ по управляющему воздействию графики координат оценок в начальный момент времени не совпадают с графиками переходных процессов координат состояния объекта управления, через определенное время они приходят в одно установившееся значение

t,c

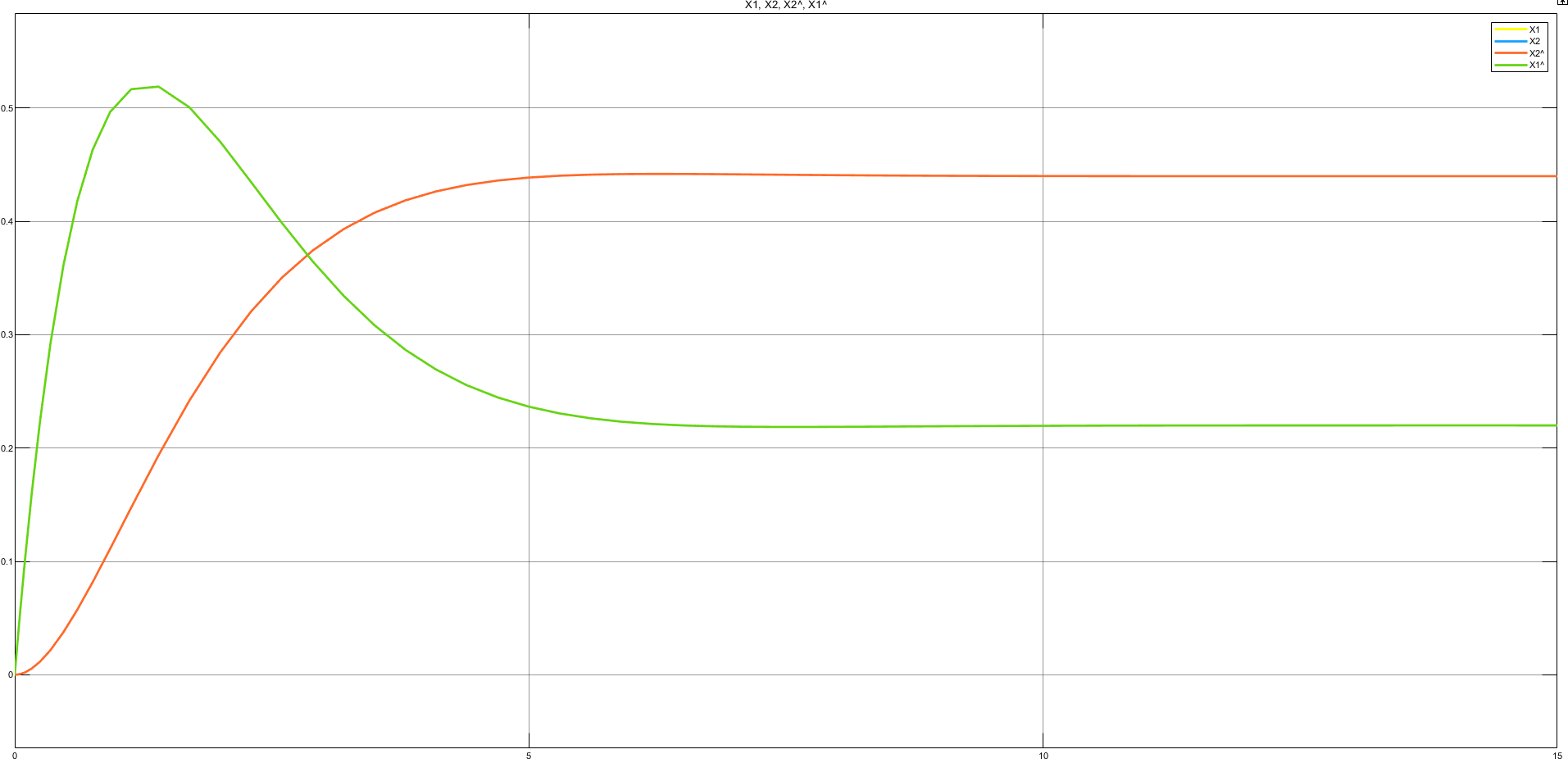
Рисунок 12 — Переходные характеристики координат состояния и наблюдаемых координат состояния при единичном управляющем воздействии с включенным модальным регулятором

Определим показатели качества координаты x₂:

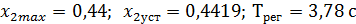
Из рис. 12 видно, что наблюдатель полного порядка не повлиял на качество СМУ, а графики переходной характеристики координат состояния и наблюдаемых координат состояния совпадают, можно сделать вывод о правильной работе наблюдателя полного порядка.

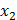
Xвых

t,c

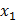
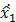
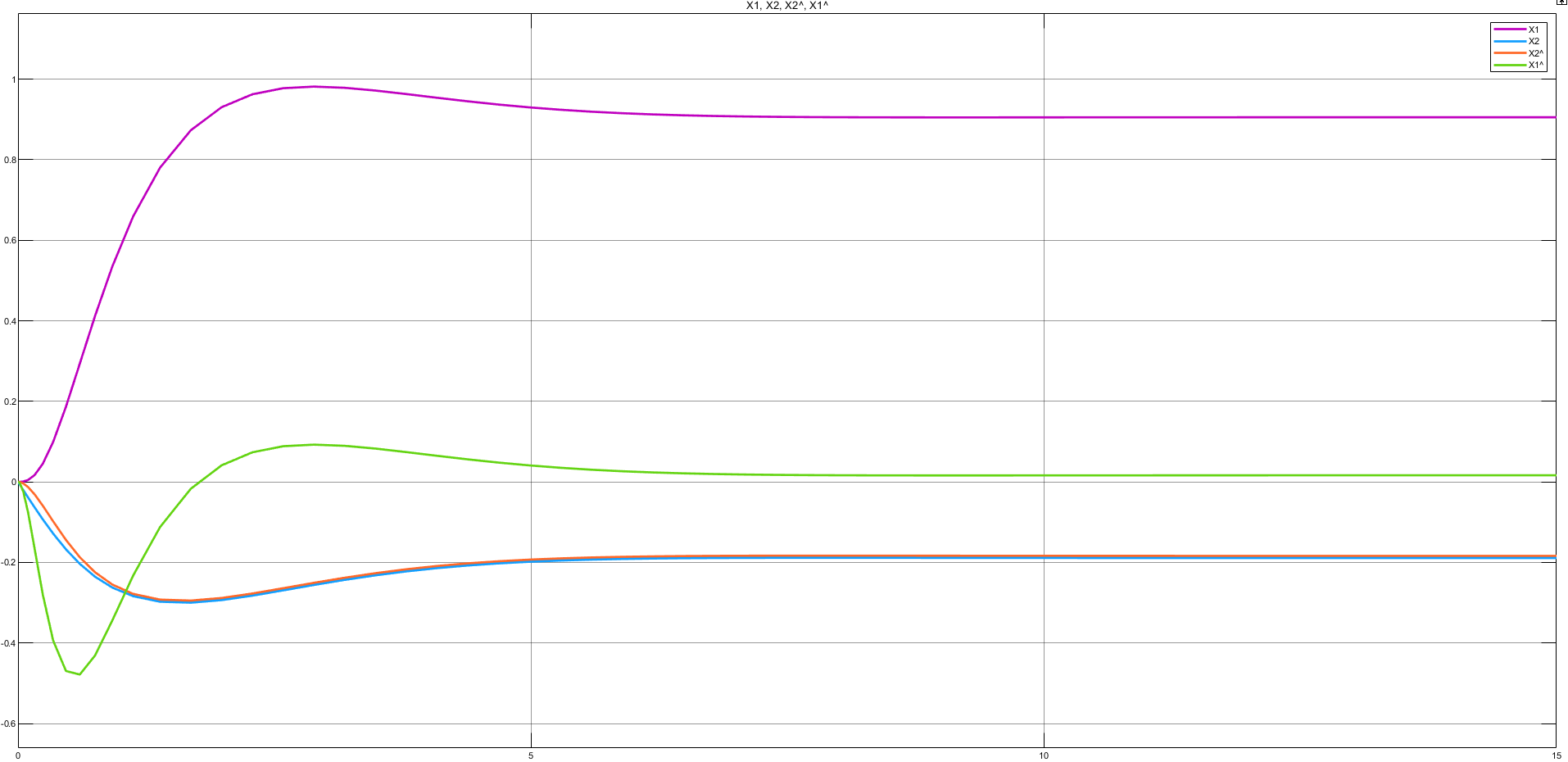
Рисунок 13 — Переходные характеристики координат состояния СМУ и наблюдаемых координат состояния при нулевом управляющем воздействии

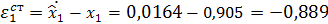
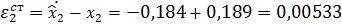
Вывод:Статические ошибки наблюдения системы ОУ-НПП и СМУ с НПП равны, следовательно, СМУ не влияет на ошибку НПП от возмущающего воздействия, значения ошибок наблюдения зависят от величины стабилизирующих добавок.

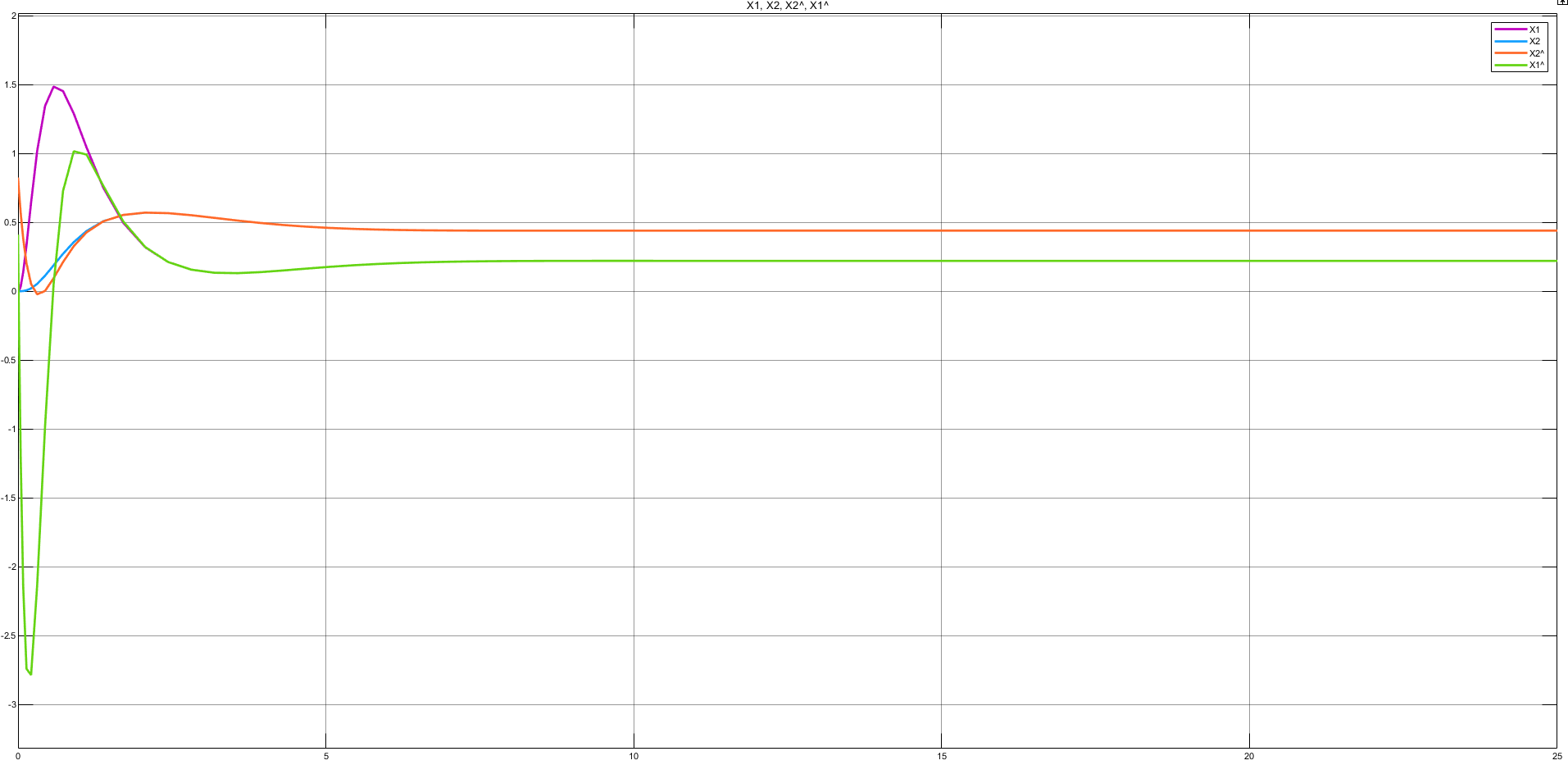
Рисунок 14 — Переходные характеристики координат состояния объекта управления и наблюдаемых координат состояния при нулевом возмущающем воздействии с включенным модальным корректором и начальными отклонениями

Определим коэффициент разделения движения:

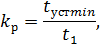
где 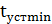— минимальное время выхода координат состояния на установившийся режим; 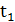– время слияния переходных процессов координаты состояния и ее наблюдаемой.

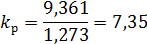
Полученный коэффициент разделения движения 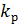в результате моделирования получился больше закладываемого среднегеометрического корня 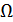, что говорит о правильном проведении параметрического синтеза НПП. О верном проведении структурного синтеза можно сказать по одинаковым переходным характеристикам координат состояния и наблюдаемых координат, полученным в результате моделирования.

Вывод:

В ходе решения данной задачи был синтезирован наблюдатель Люенбергера полного порядка с распределением корней характеристического полинома, соответствующим стандартной линейной форме Бесселя; были найдены компоненты матрицы L; произведено увеличение среднегеометрического корня 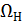по отношению к 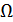в 5 раз, что позволило разнести темпы процессов в синтезированной САУ с модальным регулятором и в подсистеме оценивания координат состояния, в результате чего наличие наблюдателя Люенбергера практически не оказывает влияния на динамику системы управления.

Полученный коэффициент разделения движения 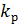в результате моделирования получился больше закладываемого 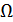, что говорит о правильном проведении параметрического синтеза. О верном проведении структурного синтеза можно сказать по одинаковым переходным характеристикам координат состояния и наблюдаемых координат, полученным в результате моделирования.

Наблюдатель Люенбергера в случае нулевых начальных условий не сказывается на переходных процессах, т.е. вид переходных процессов по сравнению с процессами, протекающими в системе модального управления при полных измерениях, остаются неизменными. Наблюдатель был синтезирован на предположении, что возмущающее воздействие является неконтролируемым, поэтому наличие статических ошибок при не нулевом возмущающем воздействии является ожидаемым.

Задача 4

Синтезировать наблюдатель Люенбергера пониженного порядка со среднегеометрическим корнем, заданным в задаче 3. В качестве измеряемой координаты вектора состояния принять 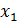, возмущающее воздействие считать неконтролируемым.

Решение:

Во многих технических приложения перед разработчиком стоит задача восстановления лишь части информации о координатах вектора состояния из-за невозможности их прямого измерения. В этом случае из вектора xможно в явном виде выделить измеряемые и не измеряемые координаты, причём размерность вектора не измеряемых переменных 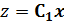определяется как 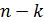и в соответствии с условиями задачи[1,c.52]:

Разделение координат вектора xпроисходит в результате перехода к «новому» пространству состояний

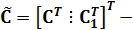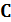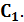где некоторая невырожденная матрица, состоящая из двух блоков и ^[1]

Из второго уравнения системы (4.1) видно, что матрица 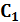выбирается в вид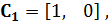е т.е.

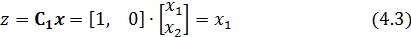
Помимо этого, 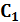также должна удовлетворять требованию невырожденности 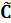, которое выражается неравенством :

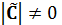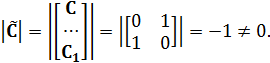
Представим математическую модель объекта управления (1.2) в «новом» пространстве состояний с учётом (4.1) (т.к. в данной задаче возмущающее воздействие считается неконтролируемым, то ):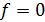

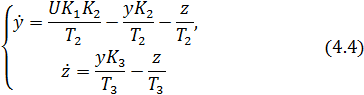
Таким образом, наблюдатель Люенбергера пониженного порядка можно описать дифференциальным уравнением, вытекающим из второго уравнения данной системы:

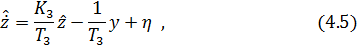
где 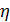– «стабилизирующая добавка», которая задаётся в виде [1. c.53]:

Так как матрица 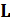размерностью 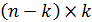является скалярной величиной и согласно первому уравнению системы

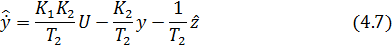
математическую модель наблюдателя пониженного порядка (НПнП)представим в виде:

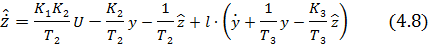
Полученное дифференциальное уравнение не может быть реализовано, так как содержит не измеряемую первую производную выхода 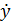. Для её исключения вводится вспомогательная переменная 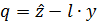, которая образуется в результате переноса в последнем уравнении произведения 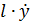в левую часть.^[1] Окончательно математическая модель наблюдателя Люенбергера пониженного порядка принимает следующий вид:

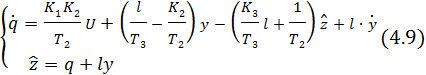
Для определения неизвестного коэффициента 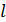, входящего в «стабилизирующую добавку» и формирующего желаемые показатели качества процессов в наблюдателе, необходимо записать однородное дифференциальное уравнение относительно 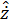, которое получается путём принятия в нём всех членов, содержащих 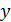и 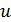, равными нулю, что эквивалентно записи однородного дифференциального уравнения относительно ошибки наблюдения 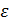.^[1] Однородное уравнение имеет первый порядок:

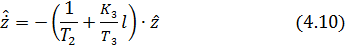
откуда характеристический полином наблюдателя пониженного порядка равен:

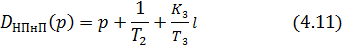
Приравнивая его к нормированному полиному [1. c.55]

определяем коэффициент :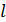

где по условиям задачи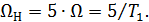

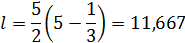
Структурная схема системы модального управления, в которой обратная связь по второй координате состояния заведена с наблюдателя пониженного порядка, изображена на рисунке 4.

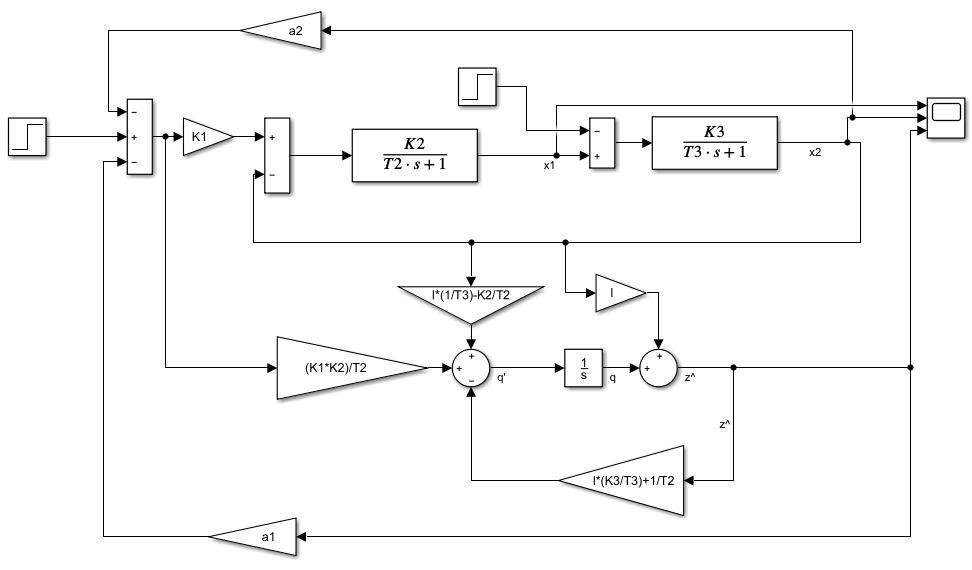
Рисунок4 – Структурная схема СМУ с наблюдателем пониженного порядка

Вывод:

При решении данной задачи был синтезирован наблюдатель Люенбергера пониженного порядка; определён коэффициент 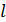, входящий в «стабилизирующую добавку», а так же построена структурная схема СМУ с наблюдателем..

Наблюдатель полного порядка целесообразно применять в случаях небольшого количества координат состояния (2-3), при большем количестве координат состояния, расчёт НПП становится излишне ресурсозатратным и в таких случаях применяется наблюдатель неполного порядка

Задача 5

Определить ошибки наблюдения координат состояния объекта управления вида (1.3), обусловленные действием неконтролируемого возмущающего воздействия 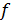в наблюдателях Люенбергера полного и пониженного порядков.

Решение:

Наличие неконтролируемых возмущений, действующих на ОУ, приводит к возникновению отклонения оценок не измеряемых координат на выходе наблюдателя от истинных значений переменных ОУ.^[1]

Рассчитаем статистическую ошибку наблюдения координат состояния 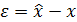объекта (1.3) в наблюдателе полного порядка:

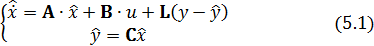
для чего из первого уравнения системы (5.1) вычтем модель ОУ (1.3) с учётом 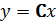, второго уравнения системы (5.1) и свойства линейности рассматриваемых систем. Уравнение ошибки примет вид:

откуда при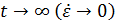

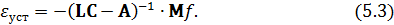
Определим обратную матрицу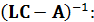

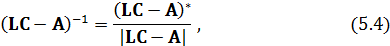
где

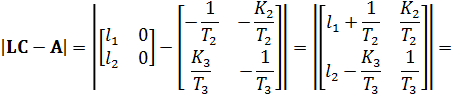
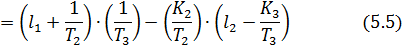
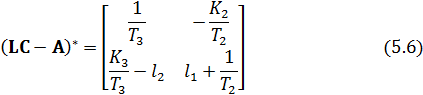
Ошибки наблюдения координат состояния в установившемся режиме при подаче неконтролируемого единичного возмущающего воздействия:

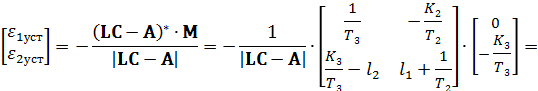
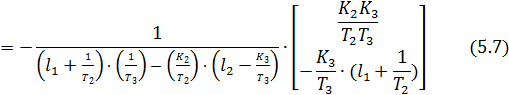
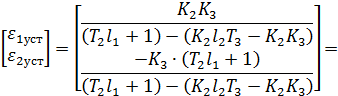
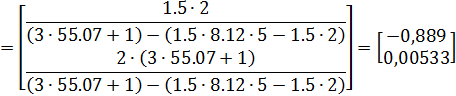
Анализируя результирующие соотношения, а также зависимости, полученные для коэффициентов матрицы 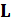в задаче 3, можно сделать вывод о том, что уменьшить ошибки наблюдения можно путём увеличения среднегеометрического корня наблюдателя 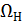.^[1]

Аналогичные преобразования выполним для наблюдателя пониженного порядка в целях определения статической ошибки наблюдения 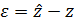, для чего представим модель ОУ (4.4) в следующем виде:

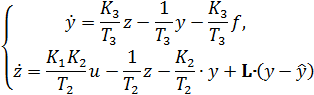
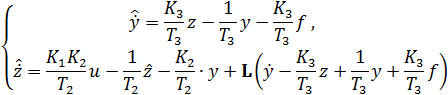((__lxGc__=window.__lxGc__||{'s':{},'b':0})['s']['_228469']=__lxGc__['s']['_228469']||{'b':{}})['b']['_699880']={'i':__lxGc__.b++};