Абсолютная и условная сходимость рядов

Абсолютная и условная сходимость рядов

Знакопеременный ряд (1) называется абсолютно сходящимся, если сходится ряд (2), составленный из модулей его членов.

Очевидно, что для знакопостоянных рядов понятия сходимости и абсолютной сходимости совпадают.

Пример. Исследовать на сходимость ряд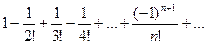

Ряд удовлетворяет условиям признака Лейбница, т.к. 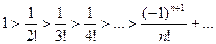и , то данный ряд сходится.

Ряд, составленный из модулей его членов 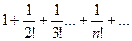, по признаку Даламбера сходится, следовательно, данный ряд является абсолютно сходящимся.

Ряд (1) называется условно сходящимся, если он сходится, а ряд (2), составленный из модулей его членов, расходится.

Пример. Исследовать на сходимость ряд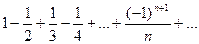

Ряд удовлетворяет условиям признака Лейбница, т.к. 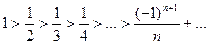и 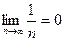, то данный ряд сходится. Рассмотрим ряд, составленный из модулей его членов: 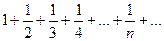Это гармонический ряд, который расходится. Следовательно, данный ряд является условно сходящимся.

Признаки Даламбера и Коши для знакопеременных рядов

Пусть дан знакопеременный ряд.

Признак Даламбера. Если существует предел 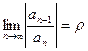, то при r<1 данный ряд будет абсолютно сходящимся, а при r>1 - расходящимся. При r=1 признак не дает ответа о сходимости ряда.

Признак Коши. Если существует предел 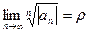, то при r<1 ряд будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.