ЕГЭ профиль 2 вариант решение. Решение.. Решение.. Решение.. Примечание.

ЕГЭ профиль 2 вариант решение

1.В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 1200 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 4 недели?

Решение.

За 4 недели в офисе расходуется 1200 · 4 = 4800 листов бумаги. Разделим 4800 на 500:

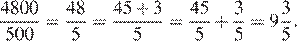
Значит, нужно купить не меньше 10 пачек бумаги.

Ответ: 10.

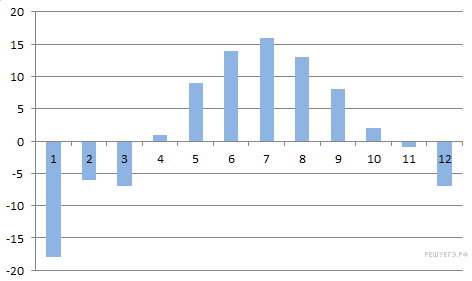
2.На диаграмме показана средняя температура воздуха (в градусах Цельсия) в Санкт-Петербурге за каждый месяц 1988 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев, когда среднемесячная температура была выше нуля.

Решение.

Из диаграммы видно, что среднемесячная температура была выше нуля в течение 7 месяцев с апреля по октябрь.

Ответ: 7.

3. 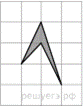Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Решение.

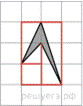Площадь четырехугольника равна разности площади большого прямоугольника, четырёх прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырехугольника и площади маленького квадрата. Поэтому

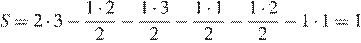
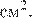
Примечание.

Заданный четырёхугольник можно рассматривать как два треугольника с общим основанием, равным длине квадратной клетки. Высоты этих треугольников равны 1, поэтому их площади 0,5, а сумма этих площадей равна 1.

4.В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.

Решение.

На первом рейсе 6 мест, всего мест 30. Тогда вероятность того, что турист П. полетит первым рейсом вертолёта, равна:

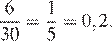
Ответ: 0,2.

5.Решите уравнение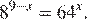

Решение.

Перейдем к одному основанию степени:

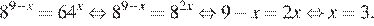
Ответ: 3.

6. 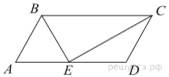Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.

Решение.

и как углы при параллельных прямых, значит, треугольник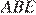и и 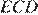– равнобедренные.

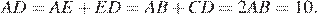
Ответ: 10.

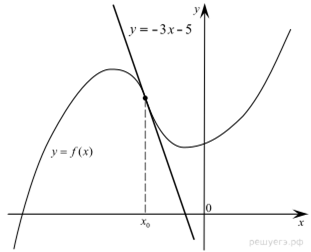
7.На рисунке изображены график функции 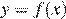и касательная к этому графику, проведённая в точке x₀. Уравнение касательной показано на рисунке. Найдите значение производной функции 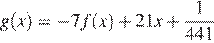в точке x₀.

Решение.

Найдём производную функции g(x):

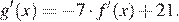
Найдём значение 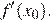Значение производной в точке касания равно угловому коэффициенту касательной.

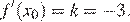
Тогда искомое значение

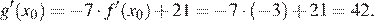
Ответ: 42.

8. 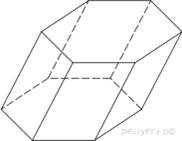Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны 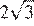и наклонены к плоскости основания под углом 30°.

Решение.

Объем призмы 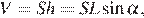где S – площадь основания, а L – длина ребра, составляющего с основанием угол α. Площадь правильного шестиугольника со стороной a равна

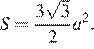
Тогда объем призмы

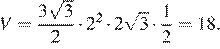
Ответ: 18.

9.Найдите 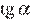, если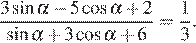

Решение.

Используем свойство пропорции:

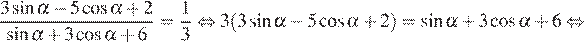
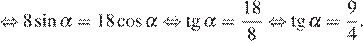
Следовательно,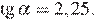

Ответ: 2,25.

10.Водолазный колокол, содержащий моля воздуха при давлении 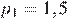атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления 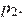Работа, совершаемая водой при сжатии воздуха, определяется выражением 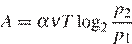, где — постоянная, 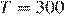К — температура воздуха. Найдите, какое давление 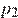(в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 6900 Дж.

Решение.

Задача сводится к решению уравнения 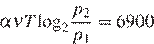при заданных значениях постоянной 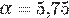, температуры воздуха 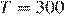К, начального давления 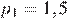атм и количества воздуха моль:

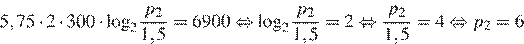атм.

Ответ: 6.

11.Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?

Решение.

Пусть t ч – время движения автомобилей до встречи. Первый автомобиль пройдет расстояние 65t км, а второй – 75t км. Тогда имеем:

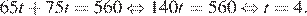
Таким образом, автомобили встретятся через 4 часа.

Ответ: 4.

12.Найдите точку минимума функции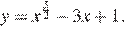

Решение.

Найдем производную заданной функции:

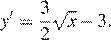
Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

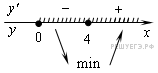
Искомая точка минимума

Ответ: 4.

13.а) Решите уравнение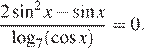

б) Найдите все корни этого уравнения, принадлежащие отрезку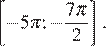

Решение.

а) Перейдём к системе: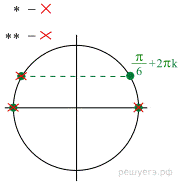

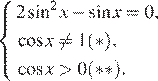
Решаем уравнение системы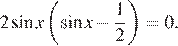

Получаем:

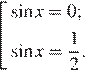
С учётом всех ограничений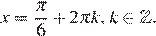

б) С помощью числовой окружности отберём корни, принадлежащие отрезку 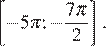Получим число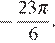

Примечание. Отбор корней может быть обоснован и любым другим способом: с помощью графика, решения двойных неравенств и т. п.

Ответ: а) 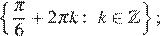б)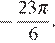

14.В правильной треугольной призме ABCA₁B₁C₁ все рёбра равны 6. На рёбрах AA₁ и CC₁ отмечены точки M и N соответственно, причём AM = 2, CN = 1.

а) Докажите, что плоскость MNB₁ разбивает призму на два многогранника, объёмы которых равны.

б) Найдите объём тетраэдра MNBB₁.

Решение.

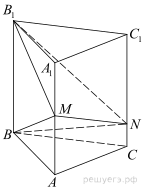Площадь основания призмы равна 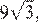а объём призмы равен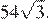

В четырёхугольной пирамиде B₁A₁C₁NM высота совпадает с высотой основания призмы A₁B₁C₁, опущенной на сторону A₁C₁, и равна 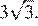Основание A₁C₁NM пирамиды B₁A₁C₁NM является трапецией, площадь которой равна 27. Значит, объём пирамиды B₁A₁C₁NM равен 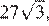то есть составляет половину объёма призмы. Поэтому объёмы многогранников B₁A₁C₁NM и ABCMB₁N равны.

б) В четырёхугольной пирамиде BACNM высота совпадает с высотой основания призмы ABC, опущенной на сторону AC, и равна 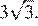Основание пирамиды BACNM является трапецией, площадь которой равна 9. Объём пирамиды BACNM равен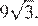

Многогранник ABCMB₁N состоит из двух частей: BACNM и MNBB₁. Значит, объём тетраэдра MNBB₁ равен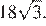

Ответ: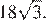

15.Решите неравенство: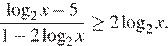

Решение.

Пусть 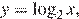получаем:

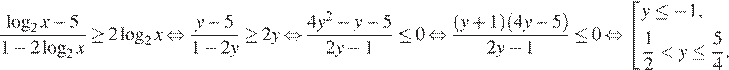
Вернёмся к исходной переменной:

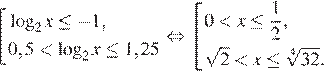
Таким образом, решение исходного неравенства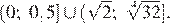

Ответ: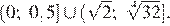

16.В прямоугольном треугольнике ABC точки M и N — середины гипотенузы AB и катета BC соответственно. Биссектриса угла BAC пересекает прямую MN в точке L.

а) Докажите, что треугольники AML и BLC подобны.

б) Найдите отношение площадей этих треугольников, если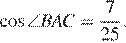

Решение.

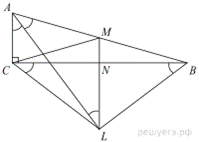а) Прямая ML параллельна прямой AC, так как содержит среднюю линию треугольника ABC (см. рисунок). Следовательно,

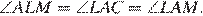
Таким образом,

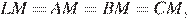
то есть точки A, B, C и L лежат на окружности с центром в точке M. Получаем:

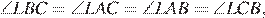
а значит, треугольники AML и BLC подобны по двум углам.

б) Углы ALB и ACB опираются на одну дугу, значит, 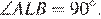Коэффициент подобия треугольников BLC и AML равен

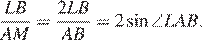
По условию

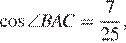
откуда

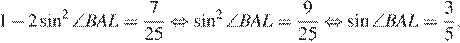
Значит, 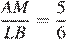и площади треугольников AML и BLC относятся как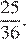

Ответ: б) 25 : 36.

17.В июле 2016 года планируется взять кредит в банке на пять лет в размере S тыс рублей. Условия его возврата таковы:

− каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;

− с февраля по июнь каждого года необходимо выплатить часть долга;

− в июле 2017,2018 и 2019 долг остаётся равным S тыс. рублей;

− выплаты в 2020 и 2021 годах равны по 360 тыс. рублей;

− к июлю 2021 долг будет выплачен полностью.

Найдите общую сумму выплат за пять лет.

Решение.

В июле 2017, 2018 и 2019 годов долг перед банком не меняется, а ежегодные выплаты составляют 0,2S тыс. рублей.

В январе 2020 года долг (в тыс. рублей) равен 1,2S, а в июле — 1,2S − 360.

В январе 2021 года долг равен 1,44S − 432, а в июле 1,44S − 792.

По условию, долг будет выплачен полностью, значит, 1,44S — 792 = 0, откуда S = 550.

Таким образом, первые три выплаты составляют по 110 тыс. рублей, а последние две — по 360 тыс. рублей.

Общая сумма выплат составляет:

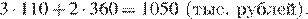
Ответ: 1050 тыс. рублей.

18.Найдите все значения 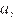при каждом из которых наименьшее значение функции

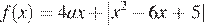
больше, чем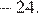

Решение.

1. При 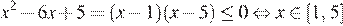функция имеет вид:

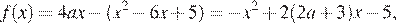
а её график представляет собой часть параболы с ветвями, направленными вниз.

При 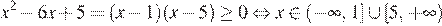функция имеет вид:

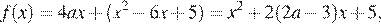
а ее график состоит из двух частей параболы с ветвями, направленными вверх и осью симметрии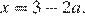

2. Если 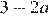принадлежит отрезку 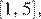то наименьшее значение функция может принимать только в точках 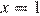и Если — то в точке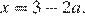

3. Наименьшее значение функции 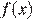больше 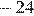тогда и только тогда, когда л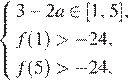ибо

либо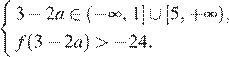

Решим первую систему:

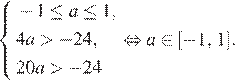
Решим вторую систему:

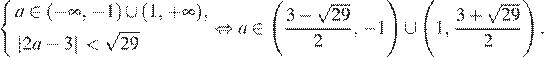
Ответ: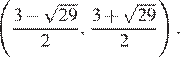

19.а) Существует ли конечная арифметическая прогрессия, состоящая из пяти натуральных чисел, такая, что сумма наибольшего и наименьшего членов этой прогрессии равна 99?

б) Конечная арифметическая прогрессия состоит из шести натуральных чисел. Сумма наибольшего и наименьшего членов этой прогрессии равна 9. Найдите все числа, из которых состоит эта прогрессия.

в) Среднее арифметическое членов конечной арифметической прогрессии, состоящей из натуральных чисел, равно 6,5. Какое наибольшее количество членов может быть в этой прогрессии?

Решение.

Без ограничения общности можно считать прогрессию возрастающей. Обозначим a — первый член прогрессии, n — количество членов, а d — её разность. Числа a, n, и d — натуральные.

а) Сумма первого и пятого членов этой прогрессии равна 2a + 4d и является чётным числом. Поскольку число 99 нечётное, сумма наибольшего и наименьшего членов конечной арифметической прогрессии из 5 натуральных чисел не может быть равной 99.

б) Сумма первого и шестого членов этой прогрессии равна 2a + 5d = 9. Поскольку d — натуральное число, получаем d — натуральное число, получаем d = 1. Тогда a = 2. Искомые числа: 2, 3, 4, 5, 6, 7.

в) Среднее арифметическое прогрессии равно полусумме её крайних членов, поэтому получаем 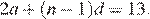Значит, 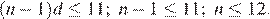Натуральны числа от 1 до 12 составляют прогрессию, среднее арифметическое членов которой равно 6,5, а количество членов равно 12. Поэтому наибольшее возможное количество чисел — это 12.

Ответ: а) нет; б) 2, 3, 4, 5, 6, 7; в)12.