Решение.. Решение.. Решение.. Решение.. Решение.. Решение.. Решение.. Решение.. Решение.. Решение.. Решение.. Решение.. Решение.. Решение.. Решение.. Решение.. Примечание.

1.Тетрадь стоит 24 рубля. Сколько рублей заплатит покупатель за 60 тетрадей, если при покупке больше 50 тетрадей магазин делает скидку 10% от стоимости всей покупки?

Решение.

За 60 тетрадей покупатель заплатил бы 60 · 24 = 1440 рублей. Скидка составит 10%, т. е. 144 рубля. Значит, покупатель заплатит 1440 − 144 = 1296 рублей.

Ответ: 1296.

2.На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев, когда среднемесячная температура была отрицательной.

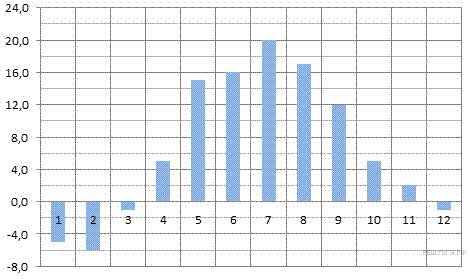
Решение.

Из диаграммы видно, что было 4 месяца с температурой ниже нуля (см. рисунок).

Ответ: 4.

3. 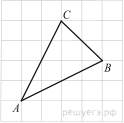На клетчатой бумаге с размером клетки 1 1 изображён треугольник ABC . Найдите длину его медианы, проведённой из вершины C.

Решение.

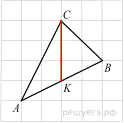Медиана проведенная из вершины C, будет делить основание AB пополам. Построим отрезок CK. Видно, что он равен 3.

Ответ: 3.

4.Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Решение.

Пусть A = «чайник прослужит больше года, но меньше двух лет», В = «чайник прослужит больше двух лет», С = «чайник прослужит ровно два года», тогда A + B + С = «чайник прослужит больше года».

События A, В и С несовместные, вероятность их суммы равна сумме вероятностей этих событий. Вероятность события С, состоящего в том, что чайник выйдет из строя ровно через два года — строго в тот же день, час и секунду — равна нулю. Тогда:

P(A + B + С) = P(A) + P(B) + P(С)= P(A) + P(B),

откуда, используя данные из условия, получаем

0,97 = P(A) + 0,89.

Тем самым, для искомой вероятности имеем:

P(A) = 0,97 − 0,89 = 0,08.

Ответ: 0,08.

5.Найдите корень уравнения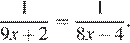

Решение.

Если две дроби с равным числителем равны, то равны их знаменатели. Имеем:

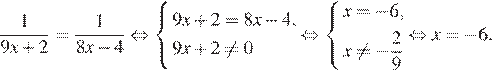
Ответ:−6.

6. 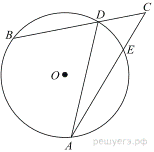Угол ACB равен 42°. Градусная величина дуги AB окружности, не содержащей точек D и E, равна 124°. Найдите угол DAE. Ответ дайте в градусах.

Решение.

Пусть искомый угол равен x. Тогда дуга DE, равна 2x. Угол между секущими CB и CA равен полуразности дуг AB и DE:

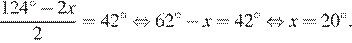
Ответ: 20.

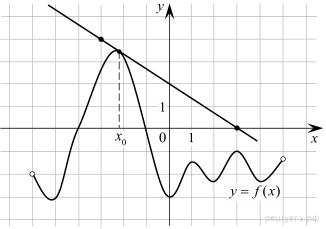
7.На рисунке изображены график функции 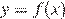и касательная к этому графику, проведённая в точке x₀. Найдите значение производной функции g(x) = 6f(x) − 3x в точке x₀.

Решение.

Найдём производную функции g(x):

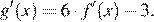
По рисунку найдём значение 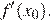Значение производной в точке касания равно угловому коэффициенту касательной, который, в свою очередь, равен тангенсу угла наклона данной касательной к оси абсцисс. Поэтому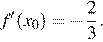

Тогда для искомого значение получаем

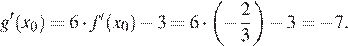
Ответ: −7.

8.Площадь поверхности правильной треугольной призмы равна 6. Какой станет площадь поверхности призмы, если все её рёбра увеличатся в три раза, а форма останется прежней?

Решение.

Площади подобных тел относятся как квадрат коэффициента подобия. Поэтому если все ребра увеличить в три раза, площадь поверхности увеличится в 9 раз. Следовательно, она станет равна 54.

Ответ: 54.

9.Найдите значение выражения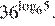

Решение.

Выполним преобразования:

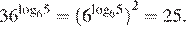
Ответ: 25.

10.Катер должен пересечь реку шириной м и со скоростью течения 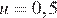м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением 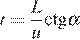, где 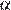– острый угол, задающий направление его движения (отсчитывается от берега). Под каким минимальным углом 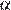(в градусах) нужно плыть, чтобы время в пути было не больше 200 с?

Решение.

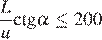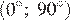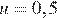Задача сводится к решению неравенства на интервале при заданных значениях длины реки м и скорости течения м/с:

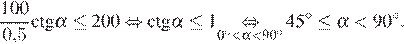
Ответ: 45.

11.Петя и Ваня выполняют одинаковый тест. Петя отвечает за час на 8 вопросов теста, а Ваня – на 9. Они одновременно начали отвечать на вопросы теста, и Петя закончил свой тест позже Вани на 20 минут. Сколько вопросов содержит тест?

Решение.

Обозначим N — число вопросов теста. Тогда время, необходимое Пете, равно 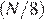часа, а время, необходимое Ване, равно 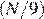часа. Петя закончил отвечать на тест через 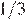часа после Вани. Поэтому:

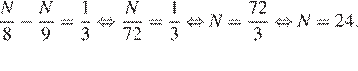
Ответ: 24.

12.Найдите точку минимума функции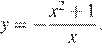

Решение.

Найдем производную заданной функции:

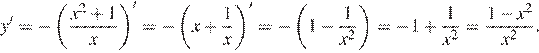
Найдем нули производной:

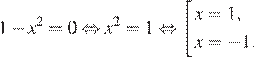
Определим знаки производной функции и изобразим на рисунке поведение функции:

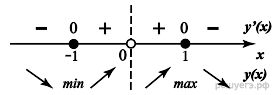
Искомая точка минимума

Ответ: −1.

13.Решите уравнение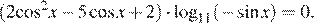

Решение.

Левая часть уравнения имеет смысл при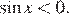

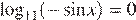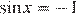Если , то , откуда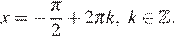

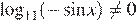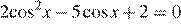Если , то , откуда 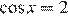или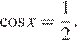

Уравнение 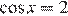не имеет решений.

Уравнение 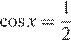имеет корни 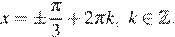Учитывая, что 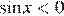, получаем: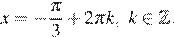

Ответ: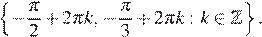

14.Ребро SA пирамиды SABC перпендикулярно плоскости основания ABC.

а) Докажите, что высота пирамиды, проведённая из точки A, делится плоскостью, проходящей через середины рёбер AB, AC и SA, пополам.

б) Найдите расстояние от вершины A до этой плоскости, если 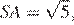AB = AC = 5,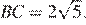

Решение.

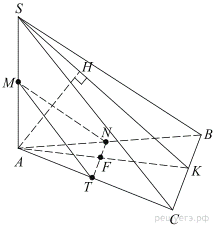
а) Пусть AH — искомая высота. Проведем SK, H 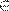SK. Проведем AK. Поскольку T и N — середины AC и AB соответственно, то TN — средняя линия треугольника ABC. Тогда TN делит AK на две равные части. Поэтому MF — средняя линия треугольника SKA, она делит AH на две равные части.

б) Поскольку AB = AC, то треугольник ABC — равнобедренный. Имеем SC = SB, следовательно, треугольник SCB тоже равнобедренный. Зная, что SA ⊥ (ABC), имеем SA ⊥ AB. Тогда треугольники SAC и SAB равны по двум сторонам и углу между ними.

Так как AC = AB, AH ⊥ (CBS), следовательно, HC ⊥ AH, AH ⊥ HB, тогда HC = HB. Значит, точка H принадлежит серединному перпендикуляру к CB, то есть SK, так как SK — медиана, высота и биссектриса равнобедренного треугольника. Тогда 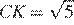, AK — биссектриса, медиана и высота равнобедренного треугольника ABC. По теореме Пифагора AK =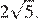

Поскольку SA ⊥ (ABC), SA ⊥ AK. Тогда по теореме Пифагора SK = 5. Имеем 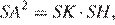то есть SH = 1. Тогда HK = 4, следовательно, AH = 2. Тогда искомое расстояние равно 1.

Ответ: б) 1.

15.Решите неравенство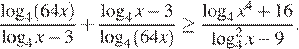

Решение.

Пусть 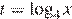, решим рациональное неравенство:

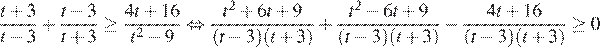
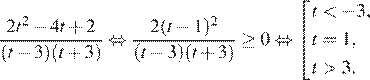
Вернёмся к исходной переменной, получим: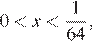

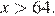
Ответ: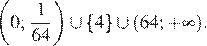

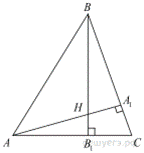
16.Высоты BB₁ и CC₁ остроугольного треугольника ABC пересекаются в точке H.

а) Докажите, что ∠AHB₁ = ∠ACB.

б) Найдите BC, если AH = 4 и ∠BAC = 60°.

Решение.

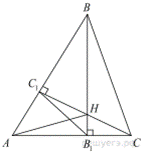а) В четырёхугольнике AC₁HB₁ углы C₁ и B₁ — прямые, следовательно, около этого четырёхугольника можно описать окружность, причём AH — её диаметр. Вписанные углы AC₁B₁ и AHB₁ опираются на одну дугу, следовательно, ∠AHB₁ = ∠AC₁B₁.

Углы BC₁C и BB₁C — прямые, значит, точки B, C, B₁ и C₁ лежат на окружности с диаметром BC. Следовательно,

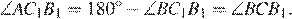
Получаем, что ∠ACB = ∠AHB₁.

б) В треугольнике AB₁C₁ диаметр описанной окружности AH = 4, откуда

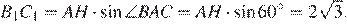
В прямоугольном треугольнике BB₁A имеем:

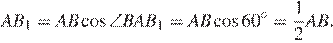
В прямоугольном треугольнике CC₁A имеем:

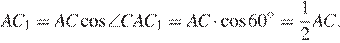
Получаем, что 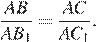Треугольники ABC и AB₁C₁ имеют общий угол A и 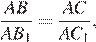следовательно, они подобны. Тогда 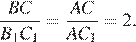Значит,

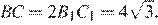
Ответ: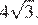

Примечание Дмитрия Гущина.

Укажем другое решение.

а) Поскольку AA₁ — перпендикуляр к ВС, а BB₁ — перпендикуляр к AС (см. рис.), углы AHB₁ и ACB равны как углы со взаимно перпендикулярными сторонами.

б) Сторона треугольника, величина противолежащего ей угла и отрезок высоты, проведённой из вершины этого угла в точку пересечения высот треугольника, связаны соотношением: 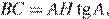откуда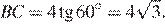

Примечание.

Рекомендуем сравнить эту задачу с заданием 519475 из экзаменационного варианта ЕГЭ 2018 года.

17.Зависимость объёма Q (в шт.) купленного у фирмы товара от цены Р (в руб. за шт.) выражается формулой 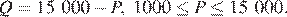Доход от продажи товара составляет РQ рублей. Затраты на производство Q единиц товара составляют 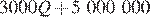рублей. Прибыль равна разности дохода от продажи товара и затрат на его производство. Стремясь привлечь внимание покупателей, фирма уменьшила цену товара на 20%, однако её прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?

Решение.

Прибыль фирмы выражается как 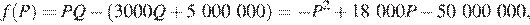то есть квадратично зависит от цены Р. Пусть первоначальная цена равнялась Р₀. После снижения цена стала равняться 0,8Р₀. Наибольшая прибыль достигается при значении Р, для которого 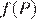достигает максимума. График функции 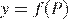— парабола с ветвями, направленными вниз, поэтому максимум 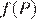достигается в вершине параболы. Поскольку 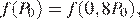вершина параболы находится в точке 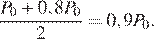Значит, нужно увеличить цену с 0,8Р₀ до 0,9Р₀, то есть на 12,5%.

Ответ: 12,5.

18.Найдите все значения 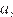при каждом из которых уравнение 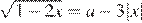имеет более двух корней.

Решение.

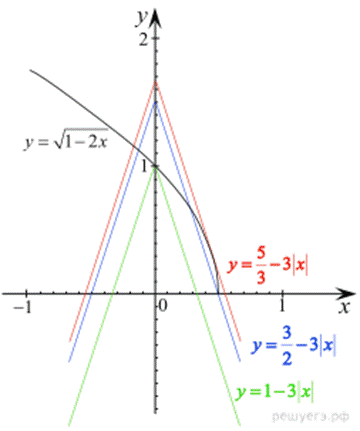Определим, что при a < 0 уравнение не имеет решений, так как левая часть не меньше нуля, а правая меньше нуля. Определим, для каких a ≥ 0 графики функци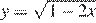и и 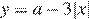имеют более двух общих точек на области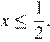

Заметим, что при всех a ≥ 1 уравнение имеет хотя бы один корень, не превосходящий нуль. При 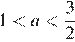уравнение имеет два решения. При 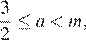где m — значение a, которому соответствует точка касания графика функции 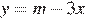и графика функции 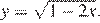Найдём m:

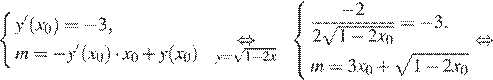
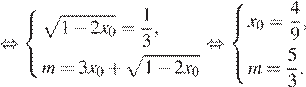
Таким образом, при 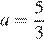уравнение имеет два решения, а при больших a — только одно решение. Значит, 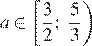— единственный промежуток, на котором уравнение имеет больше двух решений (то есть три).

Ответ: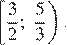

Приведём ещё одно решение:

Рассмотрим функци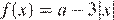и и 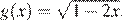Исследуем уравнение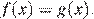

На промежутке 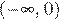функция 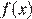возрастает. Функция 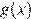убывает на этом промежутке, поэтому уравнение 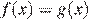имеет не более одного решения на промежутке 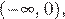причем решение будет существовать тогда и только тогда, когда, 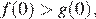то есть при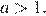

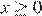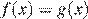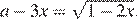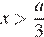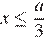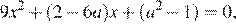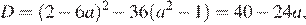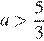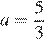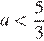При уравнение принимает вид При левая часть этого уравнения отрицательна, следовательно, решений нет. При это уравнение сводится к квадратному уравнению дискриминант которого поэтому при это уравнение не имеет корней, при — уравнение имеет единственный корень, равный при — уравнение имеет два корня.

Пусть уравнение имеет два корня, 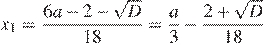и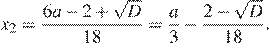

Тогда меньший корень 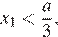а больший корень 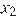не превосходит 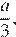если 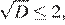то есть при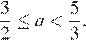

По теореме Виета 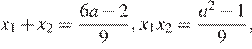поэтому знаки корне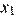й и 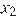зависят от знаков выражени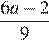й и 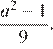Значит, при 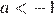оба корня отрицательны, при 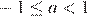один из корней отрицательный, а другой неотрицательный, при 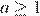оба корня неотрицательны.

Таким образом, при 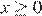уравнение 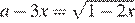не имеет корней пр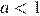и и 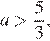имеет один корень пр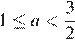и и 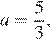имеет два корня при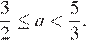

Таким образом, уравнение 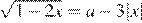имеет следующее количество корней:

— нет корней при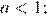

— один корень пр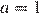и и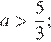

— два корня пр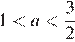и и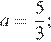

— три корня при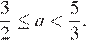

Ответ: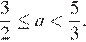

19.а) Можно ли число 2014 представить в виде суммы двух различных натуральных чисел с одинаковой суммой цифр?

б) Можно ли число 199 представить в виде суммы двух различных натуральных чисел с одинаковой суммой цифр?

в) Найдите наименьшее натуральное число, которое можно представить в виде суммы пяти различных натуральных чисел с одинаковой суммой цифр.

Решение.

а) Например числа 2006 и 8 имеют одинаковую сумму цифр и в сумме дают 2014.

б) Предположим, что число 199 можно представить в виде суммы двух натуральных чисел с одинаковой суммой цифр. Пусть одно из этих чисел состоит из a сотен, b десятков и c единиц. Тогда другое число состоит из 1 − a сотен, 9 − b десятков и 9 − c единиц. Суммы цифр этих чисел равны a + b + c и 19 − a − b − c соответственно. Они имеют разную чётность и не могут быть одинаковыми.

в) Наименьшее натуральное число, которое можно представить в виде суммы пяти различных натуральных чисел с одинаковой фиксированной суммой цифр, равно сумме пяти наименьших чисел с этой суммой цифр.

Для сумм 1, 2, 3 и 4 имеем соответственно:

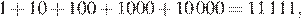
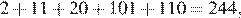
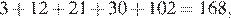
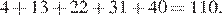
Если сумма цифр равна 5 или больше, обозначим её через a. Тогда наименьшее из таких чисел − как минимум a. Числа с одинаковой суммой цифр дают одинаковые остатки при делении на 9, поэтому идут минимум через 9. Значит, их сумма не меньше чем

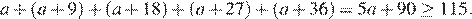
Получаем, что искомое число равно 110.

Ответ: а) да; б) нет; в) 110.