
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Обратите внимание на решение этих заданий!!!
Урок№22.Синус, косинус ,тангенс и котангенс двойного угла.
Цель занятия: - вывести формулы двойного угла; научиться применять формулы для упрощения тригонометрических выражений;
Актуализация знаний.
Обратите внимание на решение этих заданий!!!
№ 1. Вычислите:
а) 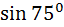 =
= 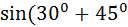 ) =
) = 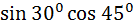 +
+ 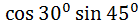 =
=
= 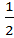
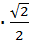 +
+ 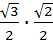 =
= 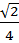 +
+ 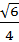 .
.
б) 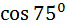 =
= 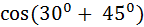 =
= 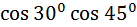 +
+ 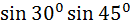 =
=
= 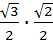 -
- 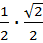 =
= 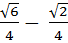 .
.
№ 2. Докажите тождество:
а) 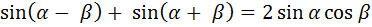 .
.
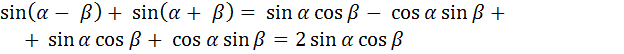 .
.
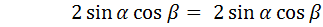 .
.
 .
.
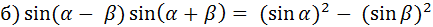 .
.
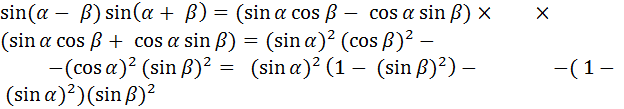 =
= 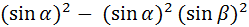 - –
- – 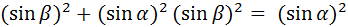 –
– 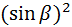 .
.
 –
– 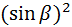 =
= 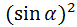 –
– 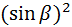 .
.
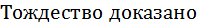 .
.
№ 3
Косинусы двух острых углов треугольника равны  и
и  . Найдите синус третьего угла.
. Найдите синус третьего угла.
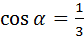 ;
; 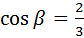 . Найти
. Найти 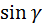 .
.
Т. к. 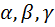 углы треугольника, то это углы I или II четверти.
углы треугольника, то это углы I или II четверти.
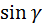 =
= 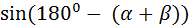 =
= 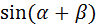 =
= 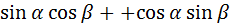 .
.
1) 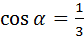
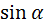 =
= 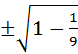 =
= 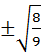 =
= 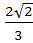 ,т.к.
,т.к. 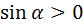 .
.
2) 
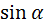 =
= 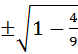 =
= 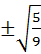 =
=  ,т.к.
,т.к. 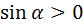 .
.
3) 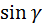 =
= 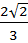
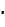
 +
+ 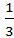
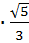 =
= 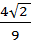 +
+ 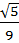 .
.
Ответ: 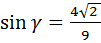 +
+ 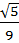 .
.
- Какие формулы применялись для выполнения заданий?
- синус и косинус суммы и разности двух углов
ПОВТОРИТЕ эти формулы !!!!!
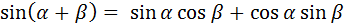

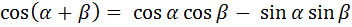
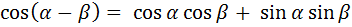
3.Изучение нового материала. 
Сегодня на занятии мы продолжим разговор о формулах сложения синуса, косинуса двух углов
На прошлом уроке мы говорили, что углы  могут быть как различными, и этот случай мы уже рассмотрели.
могут быть как различными, и этот случай мы уже рассмотрели.
- Могут ли быть углы  равными?
равными?
- да
- Какой вид примут тогда формулы сложения?
Рассмотрим формулу сложения для синуса суммы, если 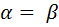
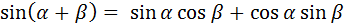
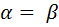
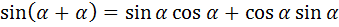
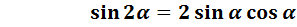
- Рассмотрите формулу сложения для косинуса суммы самостоятельно.
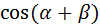 =
= 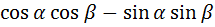
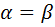
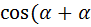 ) =
) = 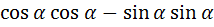
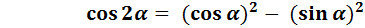
- Попробуйте дать название полученным формулам.
При возникновении затруднения в определении названия формул можно дать подсказку: сравните углы записанные в левой и правой частях тождеств.
- да, эти тождества называют формулами двойного угла.
Запишите в тетради тему урока
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|