Вариант 1. Критерий оценивания

Вариант 1

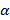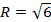1.Дан АВ – перпендикуляр к плоскости , АС и АD – наклонные, проведенные в противоположные стороны от перпендикуляра. Угол АСВ равен 30 , угол АDВ равен 60 , – радиус окружности, описанной вокруг треугольника АСD. Найдите АВ.

2.Через вершину прямого угла С в равнобедренном треугольнике DEC проведен перпендикуляр АС к плоскости данного треугольника. АС = 35 м, СD = 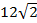м. Найдите расстояние от точки А до прямой DЕ.

3.В треугольнике со сторонами 5; 12 и 13 м, из центра вписанной окружности восстановлен перпендикуляр к плоскости треугольника. Найдите длину перпендикуляра, если расстояние от точки не принадлежащей плоскости треугольника до наибольшей стороны равно 7 м.

Критерий оценивания

№

Дескриптор

Балл

Обучающийся

Применяет признак и

свойства

перпендикулярности прямой и плоскости при решении задач

Выполняет чертеж по условию задачи

Делает вывод, что треугольник прямоугольный;

Находит длину большей стороны

Находит длины меньших сторон

Находит длину AB

Применяет теорему о трех перпендикулярах при

решении задач

Выполняет чертеж по условию задачи

Использует теорему о трех перпендикулярах

Применяет теорему о медиане прямоугольного треугольника

Находит длину необходимого отрезка

Находит расстояние от точки A до прямой DE

Применяет теорему о трех перпендикулярах при

решении задач

Выполняет чертеж по условию задачи

Указывает местоположение т. О – центра вписанной окружности

Определяет вид треугольника

Находит радиус вписанной окружности

Использует теорему о трех перпендикулярах

Находит длину перпендикуляра к плоскости треугольника

Итого