- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вариант 2. Критерий оценивания. задания
Вариант 2
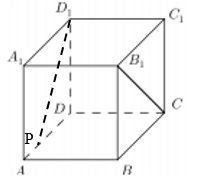
1.В кубе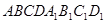 
ребро равно 1 см. 
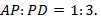Найдите угол между прямым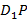и 
и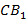 
2.Из точки проведены к плоскости две наклонные, меньшая из которых равна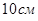 
. Проекции наклонных на плоскость равны соответственно 6 см и 
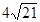см. Найдите длину большей наклонной
3.Через вершину М прямоугольного треугольника МNP с прямым углом P, проведена прямая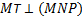 
А) докажите, что треугольник PNТ – прямоугольный
В) Найдите NТ, если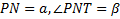 
4.Дан равнобедренный треугольник HDE: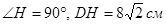 
. Через т. H проведена прямая 
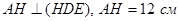. Найдите расстояние от т. A до прямой DE
Критерий оценивания
№
задания
Балл
Находит угол между двумя прямыми в пространстве
Применяет определения перпендикуляра, наклонной и проекции наклонной в пространстве при решении задач
Применяет теорему о трех перпендикулярах при решении задач