
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Проверка домашнего задания:. Решение.. Решение.. Решение.. Решение.
1. Проверка домашнего задания:
Тема: Неравенства с логарифмами по переменному основанию:
Задание № 4
Решите неравенство 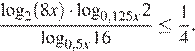
Решение.
Левая часть неравенства имеет смысл при  и
и 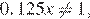 то есть при
то есть при 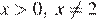 и
и 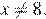 При этих условиях получаем:
При этих условиях получаем:
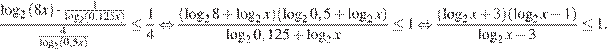
Сделаем замену 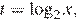 тогда
тогда
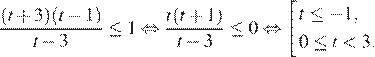
Возвращаясь к исходной переменной, получаем:
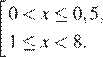
Из полученного набора нужно ещё исключить точку 2. Таким образом, множество решений исходного неравенства: 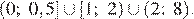
Ответ: 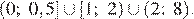
Задание № 11
Решите неравенство: 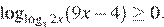
Решение.
Область допустимых значений неравенства задается соотношениями:
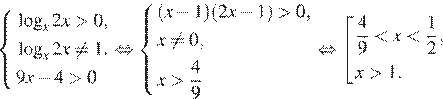
На области допустимых значений справедливы равносильности:
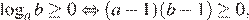
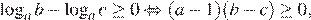
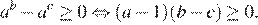
Поэтому на ОДЗ имеем:
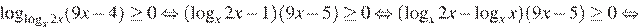
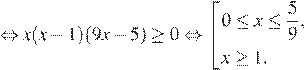
Учитывая ОДЗ получаем: 
Ответ: 
Задание № 22
Решите неравенство: 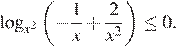
Решение.
Преобразуем неравенство: 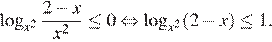
Рассмотрим два случая.
а) 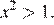
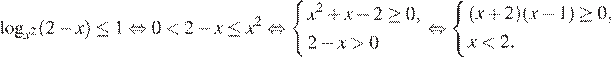
Откуда, учитывая условие 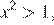 находим:
находим: 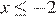 или
или 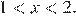
б) 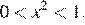
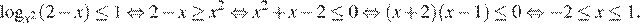
Учитывая условие 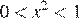 , получаем:
, получаем: 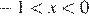 или
или 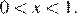
Множество решений неравенства: 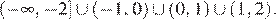
Ответ: 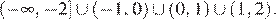
Задание № 28
Решите неравенство: 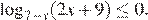
Решение.
Область допустимых значений неравенства задается соотношениями:
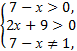 отсюда
отсюда 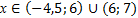
При этом можем перейти к равносильному условию:
(7-х-1)(2х+9-1)£0,
(6-х)(2х+8)£0,
(6-х)(2х+8)=0,
(6-х)=0 или (2х+8)=0
х=6 2х=-8
х=-4
Отсюда 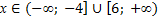 . С учетом ОДЗ получаем:
. С учетом ОДЗ получаем:
Множество решений неравенства: 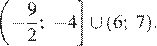
Ответ: 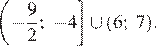
Задание № 31
Рассмотрим два случая.
Первый случай: 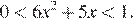 Тогда имеем систему
Тогда имеем систему
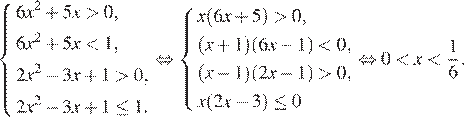
Второй случай: 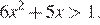 Тогда имеем систему:
Тогда имеем систему:
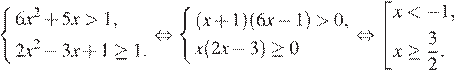
Множество решений неравенства: 
Ответ: 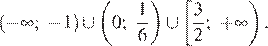
Тема: Задачи на оптимальный выбор
Задание № 18
Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 4t единиц товара.
За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей.
Григорий готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Решение.
Пусть на первом заводе работают суммарно 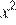 , а на втором —
, а на втором — 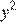 часов в неделю. Требуется найти максимум суммы
часов в неделю. Требуется найти максимум суммы 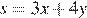 при условии
при условии
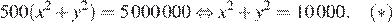
Выразим 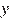 из первого соотношения:
из первого соотношения: 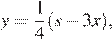 подставим в (*), получим уравнение:
подставим в (*), получим уравнение:

Полученное уравнение имеет решения, если неотрицателен его дискриминант, а значит, и четверть дискриминанта:
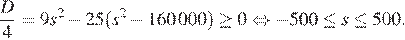
Тем самым, наибольшее возможное значение 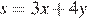 равно 500. Покажем, что оно достигается при натуральных значениях переменных: действительно, из (**) находим, что значению
равно 500. Покажем, что оно достигается при натуральных значениях переменных: действительно, из (**) находим, что значению 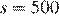 соответствует
соответствует 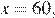 а тогда
а тогда 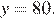
Ответ: 500 единиц товара.
Задание № 20
Производство x тыс. единиц продукции обходится в q = 0,5x2 + 2x + 5 млн рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет px − q. При каком наименьшем значении p через четыре года суммарная прибыль составит не менее 52 млн рублей?
Решение.
Прибыль (в млн рублей) за один год выражается как
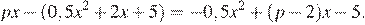
Это выражение является квадратным трёхчленом и достигает своего наибольшего значения при x = p − 2. Наибольшее значение равно 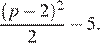 Через 4 года прибыль составит не менее 52 млн рублей при
Через 4 года прибыль составит не менее 52 млн рублей при
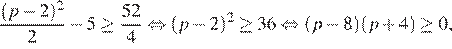
то есть при p ≥ 8, поскольку цена продукции не может быть отрицательной. Таким образом, наименьшее значение p = 8.
Ответ: p = 8 тыс. рублей.
Тема: Банки, вклады, кредиты
Задание № 77
олг перед банком (в млн рублей) по состоянию на июль должен уменьшаться до нуля равномерно:
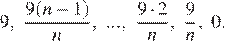
По условию, каждый январь долг возрастает на 20%, значит, последовательность размеров долга (в млн рублей) в январе такова:
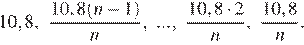
Следовательно, выплаты (в млн рублей) должны быть следующими:
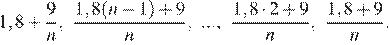
Получаем 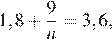 откуда
откуда 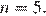 Значит, всего следует выплатить
Значит, всего следует выплатить
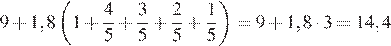 (млн рублей).
(млн рублей).
Ответ: 14,4 млн рублей.
Тема: Описанные окружности
Задание № 19
Угол C треугольника ABC, вписанного в окружность радиуса 3, равен 30°. Найдите сторону AB этого треугольника.
Решение.
По теореме синусов:
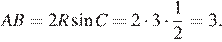
Ответ: 3.
Задание № 20
Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен 150°. Найдите радиус окружности, описанной около этого треугольника.
Решение.
Используем теорему синусов:
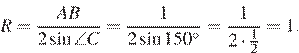
Ответ: 1.
Задание № 21
Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника.
Решение.
Для нахождения площади треугольника ABC, воспользуемся формулой Герона:
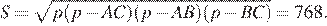
Далее по формуле 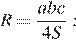

Ответ: 25.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|