Множество и его элементы

Множество и его элементы

Основоположником учения о множествах принято считать Георга Кантора (рис. 1), который в 1870 году разработал программу стандартизации математики, где любой математический объект должен был оказываться тем или иным «множеством». Однако у Кантора были и предшественники, и современники почти во всех вопросах разрабатываемой им теории. По разным причинам им не удалось получить таких серьезных результатов, каких добился Кантор.

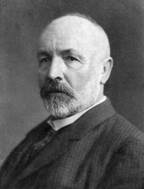
Рисунок 1. Георг Кантор (1845-1918)

«Под... множеством, – разъяснял Георг Кантор, – я понимаю вообще всякое многое, которое можно мыслить как единое, то есть всякую совокупность определенных элементов, которая может быть связана в одно целое с помощью некоторого закона...».

Множеством называют совокупность некоторых объектов. Объекты, из которых состоит множество, называют его элементами. Множества обозначают большими буквами, а элементы – маленькими.

То, что элемент a принадлежит множеству A (то есть является элементом множества A) записывают так a ∈ A, а то что элемент b не принадлежит множеству A (не является его элементом) записывают так b ∉ A.

Множество, не содержащее ни одного элемента, называется пустым и обозначается символом ∅.

Запись A⊂B (A содержится в B) означает, что каждый элемент множества A является элементом множества B; в этом случае множество А называется подмножеством множества B. Множества A и B называют равными (A=B), если A⊂B и B⊂A [9].

12 Следующая ⇒