Тест. Множества и операции над ними

Тест. Множества и операции над ними

1. На каком рисунке изображены отношения между множествами, если:

С – множество двузначных чисел,

D ={3, 34, 43, 56, 103}?

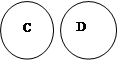
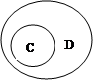
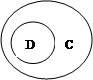
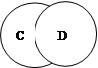
а) б) в) г)

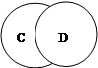
2. На каком рисунке изображены отношения между множествами, если:

С – множество двузначных чисел,

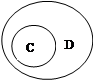
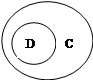D – множество натуральных чисел, не меньших 10?

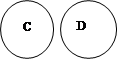а) б) в) г)

3. Какое высказывание является верным, если:

А – множество натуральных чисел, кратных 2

В – множество натуральных чисел, кратных 6?

а) А 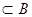б) В 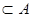в) А Ç В г) А = В

4. Пересечение множеств решений неравенств 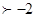х и х 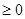изображено на рисунке

а)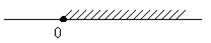

б)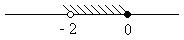

в)

г)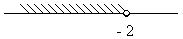

д)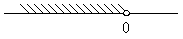

5. Объединение множеств решений неравенств 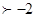х и х 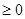изображено на рисунке

а)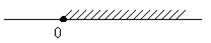

б)

в)

г)

д)

6. Объединение множеств решения неравенств х > - 5 и х ≤ 7, 5 изображено на рисунке

а)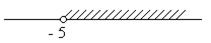

б)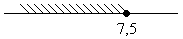

в)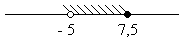

г)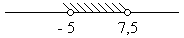

д)

7. Пересечение множеств решения неравенств х > - 5 и х ≤ 7, 5 изображено на рисунке

а)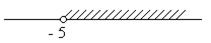

б)

в)

г)

д)

8. Какая фигура принадлежит пересечению множеств С и D, если:

С – множество ромбов;

D – множество прямоугольником.

а) ромб

б) прямоугольник

в) квадрат

9. Какие треугольники не принадлежит объединению множеств, если:

С – множество равнобедренных треугольников;

D – множество прямоугольных треугольников?

а) прямоугольные равнобедренные;

б) равнобедренные, но не прямоугольные;

в) прямоугольные, но не равнобедренные;

г) не прямоугольные и не равнобедренные.

10. Множеству Р равно множество:

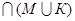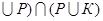а) Р б) (М в) (Р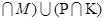

11. А – множество натуральных чисел кратных 4, С – множество натуральных чисел кратных 2. Множеству С \ А принадлежит

а) 8 б) 12 в) 26 г) 13

12. Реши задачу

Из 32 школьников 12 занимаются в волейбольной секции, 15 – в баскетбольной. 8 человек занимается и в той, и в другой секции. Сколько школьников не занимается ни в баскетбольной, ни в волейбольной секции?

а) 3 б) 13 в) 19

13. При помощи отношения « иметь один и тот же остаток при делении на 3» множество натуральных чисел разбивается на

а) два класса; б) три класса; в) четыре класса.

14. Объединением множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству

а) А и множеству В;

б) А или множеству В;

в) А, но не принадлежат множеству В;

г) В, но не принадлежат множеству А;

15. Пересечением множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству

а) А и множеству В;

б) А или множеству В;

в) А, но не принадлежат множеству В;

г) В, но не принадлежат множеству А;