Контакты

Случайная статья

Тема урока «Функции и их графики.

30.04.2020 г.

Алгебра.

9 класс

Тема урока «Функции и их графики.

Квадратичная функция и ее свойства»

Запишите в тетрадь число, классная работа, тему урока. Запишите алгоритм построения графика квадратичной функции и примеры решений заданий ГИА в тетрадь.

Алгоритм построения графика квадратичной функцииy = ах2 + bх + с

1. График функции – парабола, ветви которой направлены вверх, если а>0, вниз, если а<0.

2. Координаты вершины параболы: х₀ = 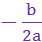, y₀ = a 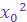+ bх₀ + с.

A(х₀;y₀)

3. Точки пересечения с осями координат:

а) с Ох: y = 0

ах² + bх + с = 0

Находим корни уравнения х₁, х_2.

В(х₁;0), С(х₂;0)

б) с Оy: х = 0

y = а 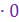+ b 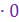+ с = c

D(0;c)

4. Дополнительные точки (при необходимости).

ГИА № 9.1

y = 4 – 3х – х²

1. График функции – парабола, ветви которой направлены вниз.

2. Координаты вершины параболы: х₀ = 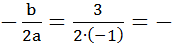1,5

y₀ = 4 – 3 1,5) 1,5)² = 4 + 4,5 2,25 = 6,25

A( 1,5; 6,25)

3. Точки пересечения с осями координат:

а) с Ох: y = 0

4 – 3х – х²= 0

х² + 3х – 4 = 0

х₁= – 4

х₂ = 1

В(– 4;0), С(1;0)

б) с Оy: х = 0

y = 4 – 3 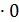– 0² = 4

D(0;4)

4. Дополнительные точки.

х	–1
y		–6

y = 4 – 3х – х²

- 4

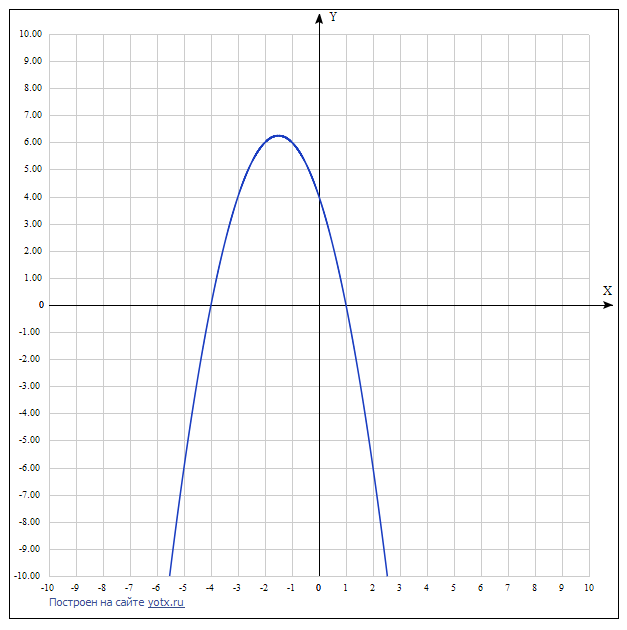
а) y>0 при x∈(-4,1)

б) y убывает при х∈[-1,5 +∞)

ГИА № 9.20

y = 2х2+ 4х – 6

1. График функции – парабола, ветви которой направлены вверх.

2. Координаты вершины параболы: х₀ = 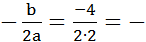1

y₀ = 2 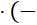1)² + 4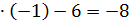

A( 1; )

3. Точки пересечения с осями координат:

а) с Ох: y = 0

2х² + 4х – 6= 0

х²+ 2х – 3 = 0

х₁= – 3

х₂ = 1

В(– 3;0), С(1;0)

б) с Оy: х = 0

y =–6

D(0;– 6)

х
y

4. Дополнительные точки.

- 8

- 6

y = 2х²+ 4х – 6

-1

- 3

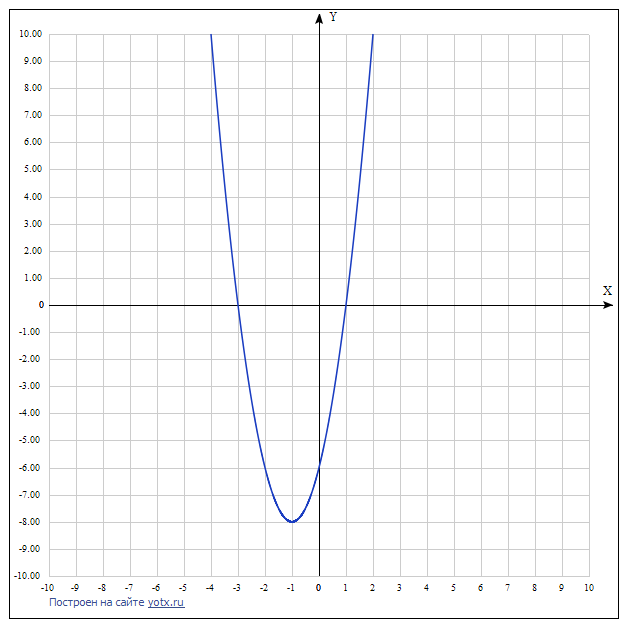
а) Е(y) = [-8; +∞)

б) yвозрастает при х∈[-1; +∞)

Домашнее задание. Решить из банка заданий ГИА № 9.2, 9.5, 9.7, 9.19.

Выслать на электронную почту.

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.