Понятие средней величины.

1. Понятие средней величины.

Средние величины и связанные с ними показатели вариации играют важную роль в статистике. Средние показатели, характеризующие всю совокупность явлений, позволяют выявить закономерности, присущие массовым социально-правовым явлениям, выявить характерные, типичные уровни изучаемых явлений и их изменения во времени и пространстве.

Средняя величина в правовой статистике– это обобщенный показатель, характеризующий типичный уровень количественно варьирующих признаков (числа судимостей, возраста и т.д.) явления в конкретных условиях места и времени. Средняя величина представляет собой именованную величину и выражается в тех же единицах измерения, что и признаки у отдельных единиц совокупности (например, размерностью при расчете среднего возраста осужденных будут годы).

Средняя величина отражает обобщенное, типичное для конкретной совокупности значение признака, присущее всем единицам совокупности, погашая при этом различия отдельных единиц.

Для того чтобы средняя величина отражала основные и действительно типические черты изучаемой совокупности, она должна рассчитываться для совокупности, состоящей из достаточно большого числа единиц, так как только в этом случае согласно закону больших чисел случайные индивидуальные различия между отдельными единицами совокупности будут нивелироваться.

Расчет средних показателей для небольшой группы данных может привести к ошибочным выводам, поскольку такие средние будут отражать значительное влияние индивидуальных особенностей, не характерных для изучаемой совокупности в целом.

Основное условие расчета средних величин – это качественная однородность единиц совокупности в отношении усредняемого признака, иначе средний показатель не будет действительно типизирующим.

Средние, рассчитанные для неоднородных совокупностей, т.е. для явлений разного типа, будут искажать различия неоднородных совокупностей или будут бессмысленными. Так, если рассчитать средний срок лишения свободы заключенных какого-либо исправительного учреждения, то получится фиктивный показатель, так как его вычисление произведено на основе разнородной совокупности, включающей в себя преступников, осужденных за различные категории преступлений (и за убийство, и за хулиганство ит.д.). В подобных случаях метод средних используется в сочетании с методом группировок. Группировки статистических показателей на основе качественных группировочных признаков позволяют выделить однородные группы, по которым и рассчитываются типические групповые средние, но мы их подробно рассматривать не будем.

2. Виды средних величин.В статистике используют различные виды средних величин, которые делятся на два больших класса:

• степенные средние (средняя гармоническая, средняя геометрическая, средняя арифметическая, средняя квадратическая, средняя кубическая);

• структурные средние (мода, медиана).

Для вычисления степенных средних необходимо использовать все имеющиеся значения признака. Мода и медиана определяются лишь структурой распределения, поэтому их называют структурными, позиционными средними. Медиану и моду часто используют как среднюю характеристику в тех совокупностях, где расчет средней степенной невозможен или нецелесообразен.

3. Самый распространенный вид средней величины – средняя арифметическая.

Под средней арифметической понимается такое значение признака, которое имела бы каждая единица совокупности, если бы общий итог всех значений признака был распределен равномерно между всеми единицами совокупности. Вычисление данной величины сводится к суммированию всех значений варьирующего признака и делению полученной суммы на общее количество единиц совокупности.

Например: 5рабочих выполняли заказ на изготовление деталей, при этом первый изготовил 5 деталей, второй – 7 деталей, третий – 4 детали, четвертый – 10 деталей, пятый– 12 деталей.

Поскольку в исходных данных значение каждого варианта встречалось только один раз, для определения средней выработки одного рабочего следует применить формулу простой средней арифметической:

т. е. в нашем примере средняя выработка одного рабочего равна

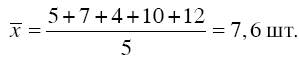
Наряду с простой средней арифметической изучают среднюю арифметическую взвешенную.

Например: рассчитаем средний возраст студентов в группе из 20 человек, возраст которых варьируется от 18 до 22 лет, где

x_i – варианты осредняемого признака,

f_i – частота, которая показывает, сколько раз встречается i-е значение в совокупности (табл. 5.1).

Таблица 5.1

Средний возраст студентов

Применяя формулу средней арифметической взвешенной, получаем: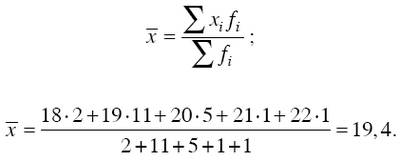

Для выбора средней арифметической взвешенной существует определенное правило: если имеется ряд данных по двум показателям, для одного из которых надо вычислить среднюю величину, и при этом известны численные значения знаменателя ее логической формулы, а значения числителя неизвестны, но могут быть найдены как произведение этих показателей, то средняя величина должна высчитываться по формуле средней арифметической взвешенной.

В некоторых случаях характер исходных статистических данных таков, что расчет средней арифметической теряет смысл и единственным обобщающим показателем может служить только другой вид средней величины – средняя гармоническая.

В настоящее время вычислительные свойства средней арифметической потеряли свою актуальность при расчете обобщающих статистических показателей в связи с повсеместным внедрением электронно-вычислительной техники.

Большое практическое значение приобрела средняя гармоническая величина, которая тоже бывает простой и взвешенной.

Если известны численные значения числителя логической формулы, а значения знаменателя неизвестны, но могут быть найдены как частное деление одного показателя на другой, то средняя величина вычисляется по формуле средней гармонической взвешенной.

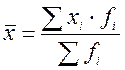
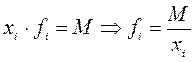
Если при использовании средней гармонической веса всех вариантов ( f ) равны, то вместо взвешенной можно использовать простую (не взвешенную) среднюю гармоническую:

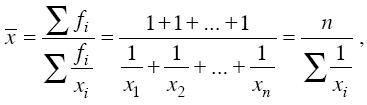
где x_i– отдельные варианты;

n– число вариантов осредняемого признака.

Любая средняя величина должна вычисляться так, чтобы при замене ею каждого варианта осредняемого признака не изменялась величина некоторого итогового, обобщающего показателя, который связан с осредняемым показателем.

Форма (формула) средней величины определяется характером (механизмом) взаимосвязи этого итогового показателя с осредняемым, поэтому итоговый показатель, величина которого не должна изменяться при замене вариантов их средней величиной, называется определяющим показателем. Для вывода формулы средней нужно составить и решить уравнение, используя взаимосвязь осредняемого показателя с определяющим.

Это уравнение строится путем замены вариантов осредняемого признака (показателя) их средней величиной.

Кроме средней арифметической и средней гармонической в статистике используются и другие виды (формы) средней величины. Все они являются частными случаями степенной средней.

Если рассчитывать все виды степенных средних величин для одних и тех же данных, то значения их окажутся одинаковыми, здесь действует правило мажорантности средних: «С увеличением показателя степени средних увеличивается и сама средняя величина».

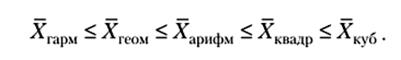
Наиболее часто применяемые в практических исследованиях формулы вычисления различных видов степенных средних величин представлены в табл. 5.2.

Таблица 5.2 Виды степенных средних

4. Средняя геометрическая применяется, когда имеется n коэффициентов роста, при этом индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики. Может обозначаться Ῡ. Средняя геометрическая характеризует, таким образом, средний коэффициент роста.

Средняя геометрическая простая рассчитывается по формуле

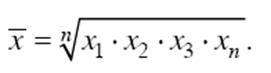
Формула средней геометрической взвешенной имеет следующий вид:

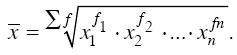
Приведенные формулы идентичны, но одна применяется при текущих коэффициентах или темпах роста, а вторая – при абсолютных значениях уровней ряда.

Ряды динамики - это значения статистических показателей, которые представлены в определенной хронологической последовательности.

Каждый динамический ряд содержит две составляющие:

1) показатели периодов времени (годы, кварталы, месяцы, дни или даты);

2) показатели, характеризующие исследуемый объект за временные периоды или на соответствующие даты, которые называют уровнями ряда.

Коэффициент роста Ki определяется как отношение данного уровня к предыдущему или базисному, показывает относительную скорость изменения ряда. Если коэффициент роста выражается в процентах, то его называют темпом роста.

Коэффициент роста

базисный - 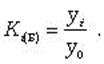цепной -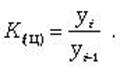

Пример: определить среднегодовой темп роста продукции предприятия.

Таблица 4.9 – Выпуск продукции предприятием в 2008-2012 гг.

Показатели	Годы
Показатели
Выпуск продукции, млн руб.	20,0 Y₁	22,0 Y₂	26,4 Y₃	50,1 Y₄	100,2 Y₅
Коэффициент роста выпуска продукции	–	1,1 k₁	1,2 k₂	1,9 k₃	2,0 k₄

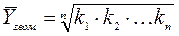(4.10)

где n – число коэффициентов роста.

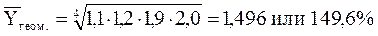
В среднем за каждый год объем продукции возрастает в 1,497 раза (или на 149,7%).

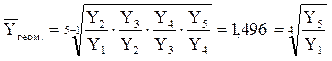(4.11)

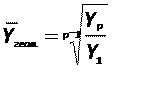(4.12)

где p – число дат (2008, 2009, 2010, 2011, 2012).

5. Средняя квадратическая применяется при расчете с величинами квадратных функций, используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической в рядах распределения и вычисляется по формуле

Средняя квадратическая взвешенная рассчитывается по другой формуле:

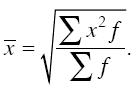
6. Средняя кубическая применяется при расчете с величинами кубических функций и вычисляется по формуле

Средняя кубическая взвешенная:

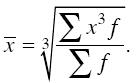
7. Все рассмотренные выше средние величины могут быть представлены в виде общей формулы:

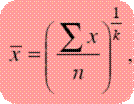где – средняя величина; Х– индивидуальное значение; n – число единиц изучаемой совокупности; k – показатель степени, определяющий вид средней.

При использовании одних и тех же исходных данных, чем больше k в общей формуле степенной средней, тем больше средняя величина. Из этого следует, что между величинами степенных средних существует закономерное соотношение, о котором уже указывалось выше ( правило мажорантности):

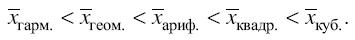
8. Средние величины, описанные выше, дают обобщенное представление об изучаемой совокупности и с этой точки зрения их теоретическое, прикладное и познавательное значение бесспорно. Но бывает, что величина средней не совпадает ни с одним из реально существующих вариантов, поэтому кроме рассмотренных средних в статистическом анализе целесообразно использовать величины конкретных вариантов, занимающие в упорядоченном (ранжированном) ряду значений признака вполне определенное положение. Среди таких величин наиболее употребительными являются структурные, или описательные, средние – мода (Мо) и медиана (Ме).

9. Мода– величина признака, которая чаще всего встречается в данной совокупности. Применительно к вариационному ряду модой является наиболее часто встречающееся значение ранжированного ряда, т. е. вариант, обладающий наибольшей частотой. Мода может применяться при определении магазинов, которые чаще посещаются, наиболее распространенной цены на какой-либо товар. Она показывает размер признака, свойственный значительной части совокупности, и определяется по формуле

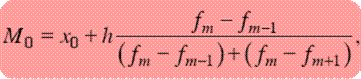
где х₀ – нижняя граница интервала;

h – величина интервала;

f_m – частота интервала;

f_{m_}₁ – частота предшествующего интервала;

f_m+₁ – частота следующего интервала.

Для дискретных рядов мода определяется визуально.

Пример: определить моду следующего ряда распределения.

Таблица 4.10 – Данные о проданных парах обуви, ед.

Размер обуви (х)	Число проданных пар (f)	Накопленные частоты (cum f)

		12 (2 + 10)
		32 (12 + 20)
37	88	120 (32 + 88)
		139 (120 + 19)
		148 (139 + 9)
		150 (148 + 2)
Итого	150	–

Модой является размер 37, т.е. наибольшее число проданной обуви было 37-го размера.

Новый термин «накопленные частоты» -что означает: к предыдущей частоте прибавляем следующую за ней. В таблице эти операции указаны действиями.

10. Медианой называется вариант, расположенный в центре ранжированного ряда. Медиана делит ряд на две равные части таким образом, что по обе стороны от нее находится одинаковое количество единиц совокупности. При этом у одной половины единиц совокупности значение варьирующего признака меньше медианы, у другой – больше ее.

Медиана используется при изучении элемента, значение которого больше или равно или одновременно меньше или равно половине элементов ряда распределения. Медиана дает общее представление о том, где сосредоточены значения признака, иными словами, где находится их центр.

Описательный характер медианы проявляется в том, что она характеризует количественную границу значений варьирующего признака, которыми обладает половина единиц совокупности. Задача нахождения медианы для дискретного (целые числа) вариационного ряда решается просто. Если всем единицам ряда придать порядковые номера, то порядковый номер медианного варианта определяется как с нечетным числом членов n.

Если же количество членов ряда является четным числом, то медианой будет являться среднее значение двух вариантов, имеющих порядковые номера n / 2 и n / 2 + 1.

Для ранжированного ряда (ряд упорядоченных числовых значений, в котором числа расположены в определенном логическом порядке, либо порядке возрастания, либо порядке убывания) с нечетным числом индивидуальных величин (например, 1, 2, 3, 6, 7, 9, 10) медианой будет величина, которая расположена в центреряда, т.е. четвёртая величина - 6.

Для ранжированного ряда с четным числом индивидуальных величин (например, 1, 5, 7, 10, 11, 14) медианой будет средняя арифметическая величина, которая рассчитывается из двух смежных величин. Для нашего случая медиана равна (7+10) = 8,5.

При определении медианы в интервальных вариационных рядах сначала определяется интервал, в котором она находится (медианный интервал). Этот интервал характерен тем, что его накопленная сумма частот равна или превышает полусумму всех частот ряда. Расчет медианы интервального вариационного ряда производится по формуле

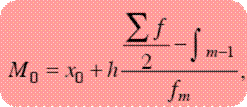
где X₀– нижняя граница интервала;

h– величина интервала;

f_m – частота интервала; f– число членов ряда;

f_m-1 – сумма накопленных членов ряда, предшествующих данному.

Наряду с медианой для более полной характеристики структуры изучаемой совокупности применяют и другие значения вариантов, занимающих в ранжированном ряду вполне определенное положение. К ним относятся квартили и децили. Квартили делят ряд по сумме частот на 4 равные части, а децили – на 10 равных частей. Квартилей насчитывается три, а децилей – девять.

Медианаи мода в отличие от средней арифметической не погашают индивидуальных различий в значениях варьирующего признака и поэтому являются дополнительными и очень важными характеристиками статистической совокупности. На практике они часто используются вместо средней либо наряду с ней. Особенно целесообразно вычислять медиану и моду в тех случаях, когда изучаемая совокупность содержит некоторое количество единиц с очень большим или очень малым значением варьирующего признака. Эти, не очень характерные для совокупности значения вариантов, влияя на величину средней арифметической, не влияют на значения медианы и моды, что делает последние очень ценными для экономико-статистического анализа показателями.

Контрольные вопросы и задания

1. В чем заключается сущность статистической обработки методом средней величины?

2. В каких случаях применяется средняя арифметическая простая? В чем ее отличие от средней арифметической взвешенной?

3. Назовите виды средних степенных величин и напишите формулу степенной средней.

4. Являются ли мода и медиана средними величинами и почему?

5. Как определить моду и медиану для дискретного ряда?