
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лекция по Математике (ТС-1) Тема 3.2.
Лекция по Математике (ТС-1) Тема 3.2.
Область определения функции, заданной аналитически. Графики функций.
у = х (Линейная функция) у = х2 (Квадратичная функция. Парабола)
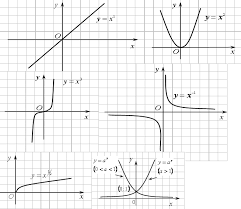
у = х3 у = у = х-3
(кубическая у = 1 /х3
парабола)
у = х1/2
у= 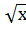
квадратный
корень
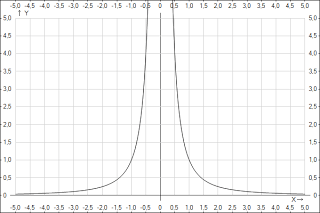 у = х1/3
у = х1/3
у= х-2 у= 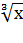
у=х1/2 кубический корень
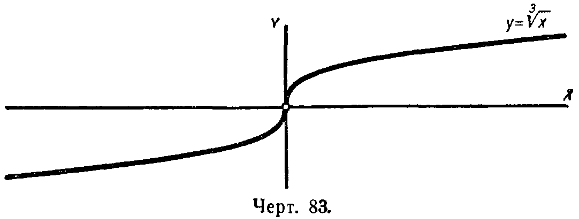
Область определения функции
Если функция задана формулой и область определения функции не указана, то считают, что её область определения состоит из всех значений независимой переменной, при которой эта формула имеет смысл.
1. Целые функции. Формула содержит действия +, -, *, (), 2.
Областью определения является любое действительное число. D= 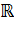 , D= (-
, D= (- 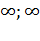 )
)
2. Дробно-рациональные функции. Формула содержит +, -, *, (), 2, / .
F(x) = U(x) / V(x). Область определения D: V(x) 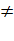 0
0
3. Иррациональныефункции F(x) = 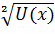 Область определения D: U(x) ≥ 0
Область определения D: U(x) ≥ 0
При делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный.
Свойства функции: Монотонность, ограниченность, четность и нечетность и периодичность функции.
1) МОНОТОННОСТЬ
Рассмотрим графики функции. Выберем произвольное значение аргумента и найдем соответствующее значение функции.
Монотонность
Возрастающая
Большему значению аргумента соответствует большее значение функции х1 < x2, f(x1) < f(x2)
f(x) ↑ функция возрастает
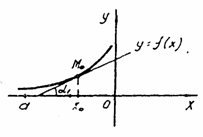 Рис.1
Рис.1
| Убывающая
Большему значению аргумента соответствует меньшее значение функции х1 < x2 f(x1) > f(x2)
f(x) ↓ функция убывает
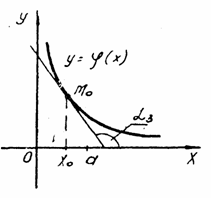 Рис.2 Рис.2
|
Опр. Функция только возрастающая или только убывающая называется МОНОТОННОЙ, (Рис 1,2)
Немонотонная функция – возрастаюшая и убывающая. Пример. Парабола
f(x) ↓ , x Î (- 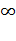 ,0) f(x) ↑ , (0; +
,0) f(x) ↑ , (0; +  )
)
Промежутки на которых функция возрастает или убывает называют промежутками монотонности.
2) ЧЕТНОСТЬ И НЕЧЕТНОСТЬ
Четная функция у = х2
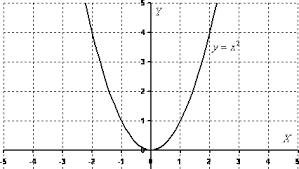 f(-x) = f(x)
f(x) – четная
График четной функции симметричен относительно оси ординат (у).
f(-x) = f(x)
f(x) – четная
График четной функции симметричен относительно оси ординат (у).
| Нечетная функция у = х3
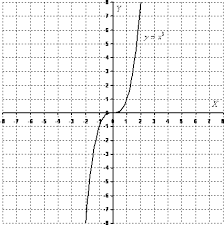 f(-x) = -f(x)
f(x) – нечетная
График нечетной функции симметричен относительно начала координат т.О.
f(-x) = -f(x)
f(x) – нечетная
График нечетной функции симметричен относительно начала координат т.О.
|
Большинство функций являются ни четными ни нечетными – функции общего вида.
Порядок выполнения отчета по лекции.
(ЛЕКЦИЮ ЗАКОНСПЕКТИРОВАТЬ В ТЕТРАДИ, прислать по ссылке в виде фото https://vk.com/public193953220) илина эл. почту Lena_Danukova@Mail.ru
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|