Тема: Целые и рациональные числа

Тема: Целые и рациональные числа

Дата: 06.10.2020 г.

Группа: МОЦИ-264

Студенты должны знать: что такое натуральное, целое, рациональное число, периодическая дробь.

Студенты должны уметь:записывать бесконечную десятичную дробь в виде обыкновенной, выполнять действия с десятичными и обыкновенными дробями.

Теоретическая часть.

1. Первоначально под числом понимали лишь натуральные числа. Которых достаточно для счёта отдельных предметов.

Множество N ={1; 2; 3...} натуральных чисел замкнуто относительно операций сложения и умножения. Это значит, что сумма и произведение натуральных чисел являются числами натуральными.

2. Однако разность двух натуральных чисел уже не всегда является натуральным числом.

Примеры: 1) 5 – 5 = 0; 2) 5 – 7 = – 2,

числа 0 и – 2 не являются натуральными.

Так, результат вычитания двух одинаковых натуральных чисел приводит к понятию нуля и введению множества целых неотрицательных чисел

Z₀={0; 1; 2;...}.

3. Чтобы сделать выполнимой операцию вычитания, вводят отрицательные целые числа, то есть числа, противоположные натуральным. Таким образом получают множество целых чисел Z ={...; -3; -2; -1; 0; 1; 2;...}.

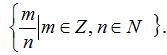Чтобы сделать выполнимой операцию деления на любое число, не равное нулю, необходимо к множеству всех целых чисел присоединить множество всех положительных и отрицательных дробей. В результате получается множество рациональных чисел

Q =

При выполнении четырёх арифметических действий (кроме деления на нуль) над рациональными числами всегда получаются рациональные числа.

4. Каждое рациональное число можно представить в виде периодической десятичной дроби.

Вспомним, что такое периодическая дробь. Это бесконечная десятичная дробь, у которой начиная с некоторого десятичного знака повторяется одна и та же цифра или несколько цифр – период дроби. Например, 0,3333…= 0,(3);

1,057373…=1,05(73).

Читаются эти дроби так: “0 целых и 3 в периоде”, “1 целая, 5 сотых и 73 в периоде”.

Запишем рациональные числа в виде бесконечной периодической десятичной дроби:

натуральное число 25 = 25,00…= 25,(0);

целое число -7 = -7,00…= -7,(0);

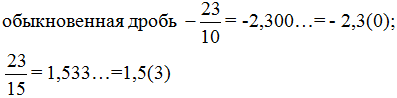
(пользуемся алгоритмом деления уголком).

5. Справедливо и обратное утверждение: каждая бесконечная периодическая десятичная дробь является рациональным числом, так как может быть представлена в виде дроби 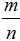, где m – целое число, n – натуральное число.

Рассмотрим пример:

1) Пусть x= 0,2(18) умножая на 10, получаем 10x = 2,1818…

(Нужно умножить дробь на 10ⁿ, где n – количество десятичных знаков, содержащихся в записи этой дроби до периода: x10ⁿ).

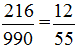2) Умножая обе части последнего равенства на 100, находим 1000x = 218,1818…(Умножая на 10^k, где k – количество цифр в периоде x10ⁿ10^k= x10^n+k).

3) Вычитая из равенства (2) равенство (1), получаем 990x = 216, х=

12 Следующая ⇒