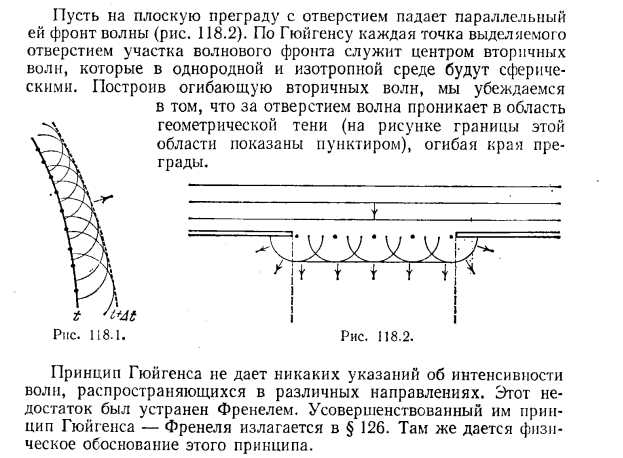
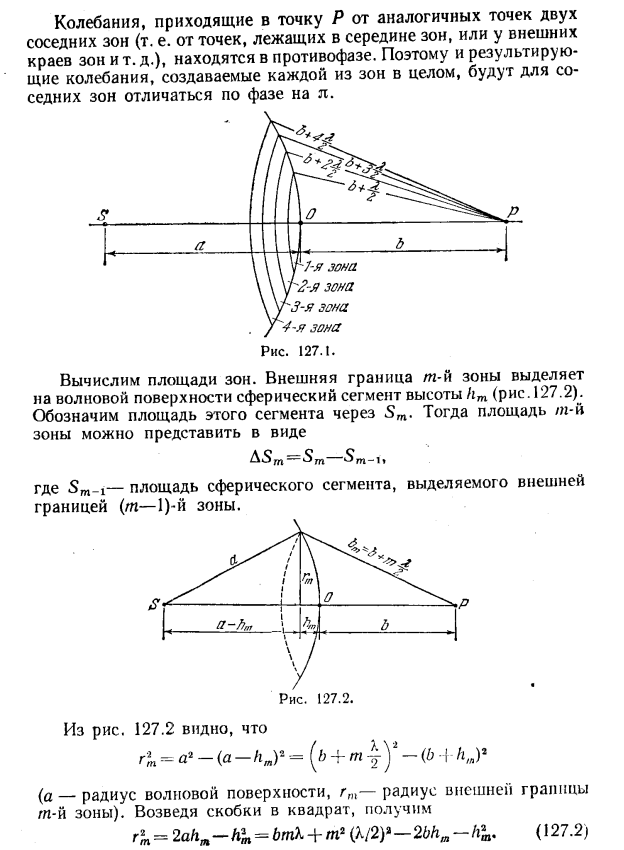
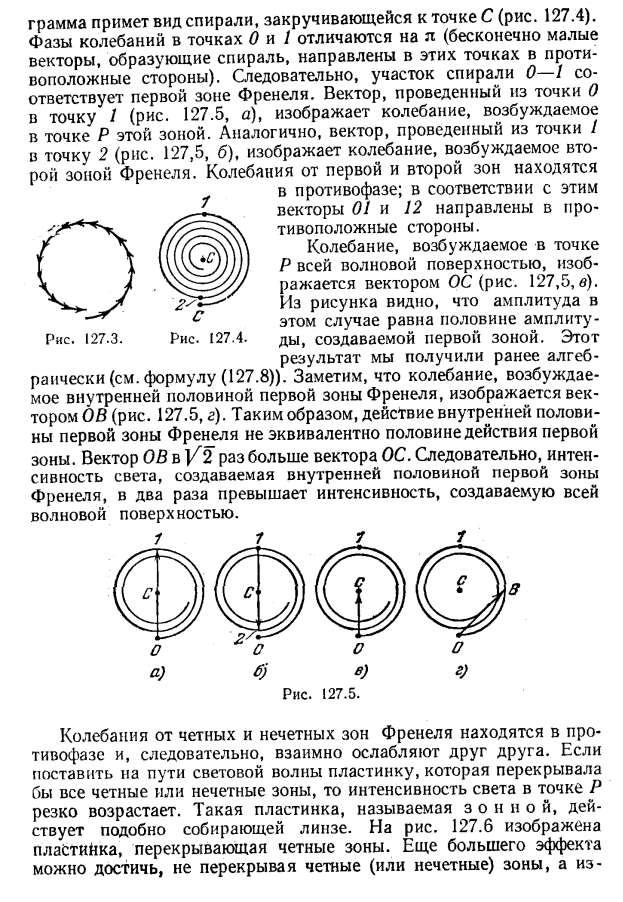
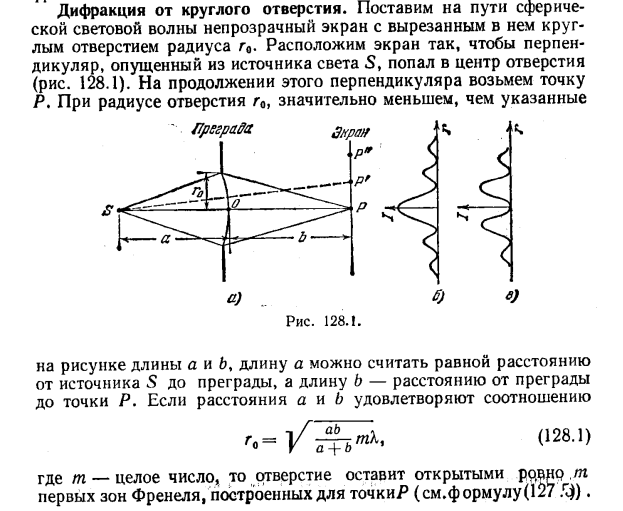
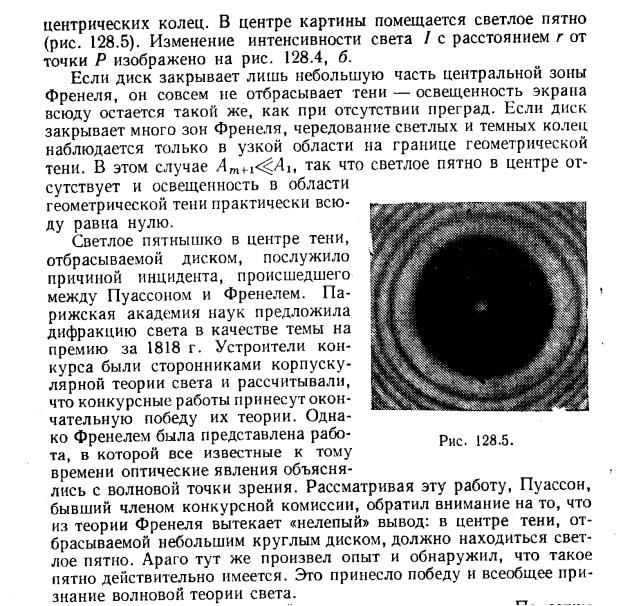
Дифракция света.. План лекции. I. Принцип Гюйгенса-Френеля. Дифракция Френеля. Метод зон Френеля. Зоны Френеля. Спираль Френеля. Зонная пластинка. II. Дифракция Френеля на простейших преградах: круглом отверстии, круглом диске. Пятно Пуассона.. III. Ди

ЛЕКЦИЯ 13

Дифракция света.

План лекции

I. Принцип Гюйгенса-Френеля. Дифракция Френеля. Метод зон Френеля. Зоны Френеля. Спираль Френеля. Зонная пластинка..

II. Дифракция Френеля на простейших преградах: круглом отверстии, круглом диске. Пятно Пуассона.

III. Дифракция на краю полубесконечного экрана. Спираль Корню. Недостатки метода зон Френеля.

I. Принцип Гюйгенса-Френеля. Дифракция Френеля. Метод зон Френеля. Зоны Френеля. Спираль Френеля. Зонная пластинка.

Дифракция на краю полубесконечного экрана. Спираль Корню. Недостатки метода зон Френеля.

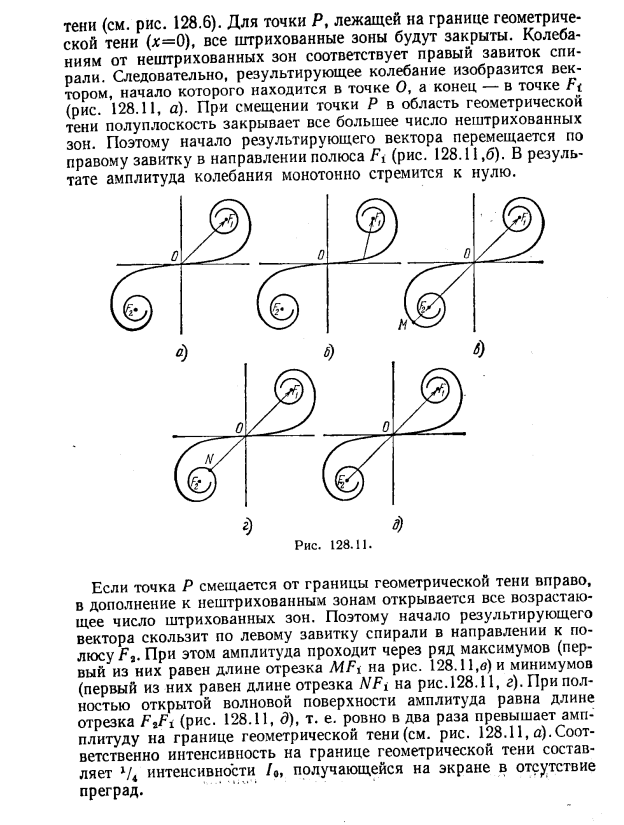
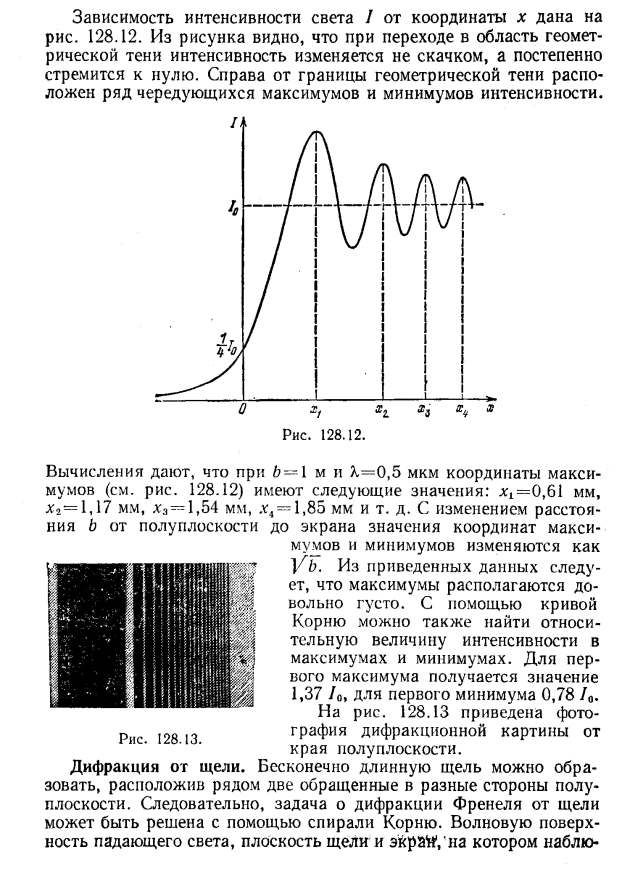
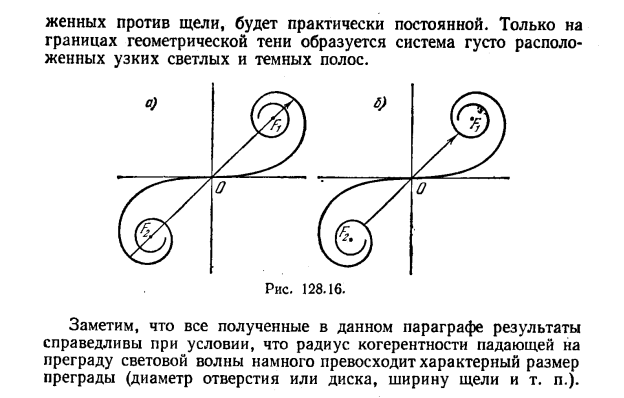
При этом, однако, в методе расчета Френеля есть принципиальные неясности. Главные из них заключаются в следующем.

1. При вычислении результатов интерференции элементарных волн приходится считать, что амплитуда колебаний от элементов dS волновой поверхности зависит от угла 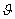между нормалью к элементу dS и направлением на точку Р, для которой ведется расчет. Амплитуда максимальна при 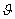= 0 и монотонно убывает до нуля при стремлении 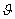к π/2, т. е. нет обратной волны. Это обстоятельство остается не обоснованным в теории Френеля.

2. Расчет по методу Френеля дает неправильное значение фазы результирующего колебания. Для полностью открытой волновой поверхности она отличается на π/2 от действительной. Это видно из рисунка спирали Френеля. Направление спирали Френеля в ее начале дает в точке наблюдения фазу колебаний от центрального элемента первой зоны. Это и есть то значение фазы, которое соответствует действительности. Результирующий же вектор от полностью открытой волновой поверхности повернут на π/2 против часовой стрелки, т. е. отстает по фазе на π/2. Таким образом, постулат Френеля, правильно задавая амплитуды вспомогательных источников, неудачно определяет их фазы.

Однако, для большинства задач вопрос о фазе не имеет значения, ибо нас интересует интенсивность результирующей волны, которая пропорциональна квадрату амплитуды. Значение же интенсивности метод Френеля дает правильное.

Итак, несмотря на некоторые недостатки, метод Френеля в вопросах расчета интенсивности волн для многих случаев является весьма плодотворным.