Дифракция света.

2. Дифракция света.

Характерным для распространения любых волн является их способность загибать за преграды (давать дифракцию). Однако масштаб загибания зависит от отношения размеров преграды к длине волны. Например, крупные волны, распространяющиеся по поверхности воды, полностью огибают сваю, мелкая же рябь образует за сваей хорошо выраженную область „тени".

Если мы поставим за отверстием белый экран, который будем приближать к отверстию или удалять от него, то центр экрана будет становиться по мере перемещения то темным, то светлым. Из закона сохранения энергии можно далее заключить, что и боковые точки (расположенные в стороне от оси ОР) должны быть попеременно, то светлыми, то темными: центральное пятно будет окружено рядом светлых и темных колец.

Разобранный случай дифракции наблюдаются без помощи каких-либо оптических приборов: на пути фронта световой волны располагается лишь непрозрачный экран, частично загораживающий фронт. Данный вид дифракции называется дифракцией Френеля.

Иной способ наблюдения дифракционных явлений дал Фраунгофер. Он наблюдал картину, возникшую в главной фокальной плоскости линзы, собирающей плоские световые волны, частично загороженные тем или иным непрозрачным экраном. Данный вид дифракции называется дифракцией Фраунгофера.

Рассмотрим частный случай дифракции Фраунгофера – дифракцию от одной щели. Принципиальная схема наблюдения дифракции плоских волн (дифракция Фраунгофера) представлена на рисунке. Излучение точечного источника A превращается линзой L₁ в плоскую волну, которая проходит через щель в непрозрачном экране Э. Линза L₂ собирает в различных участках своей главной фокальной плоскости все лучи, прошедшие через щель, в том числе и отклонившиеся на угол j от первоначального направления в результате дифракции. Исследуя распределение освещенности в фокальной плоскости линзы L₂, можно определить видимость дифракционной картины.

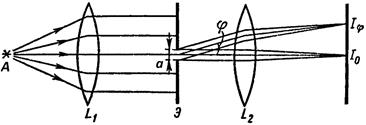
Применение метода Гюйгенса – Френеля в данном случае весьма просто. Будем считать, что воображаемая поверхность S совпадает с плоскостью непрозрачного экрана и целиком закрывает щель. В наиболее простом случае – нормальное падение исходной волны на поверхность экрана – дополнительная разность хода лучей от различных участков щели определяется углом наблюдения j.

Для того чтобы определить разность хода между двумя колебаниями, достаточно из точки на поверхности щели, через которую проходит один луч, опустить перпендикуляр на другой луч. Тогда расстояние по этому второму лучу от плоскости щели до основания перпендикуляра и будет искомой разностью хода. В данном случае зоны Френеля, очевидно, будут иметь вид прямоугольных полосок, параллельных краям щели. Число зон Френеля будет зависеть от ширины щели а, угла наблюдения j и длины волны l. Поскольку разность хода между лучами, проходящими через края одной зоны Френеля, равна l/2, из геометрических соображений легко получить, что ширина зоны будет равна 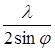(разность хода – катет, ширина зоны – гипотенуза). Число зон Френеля n, укладывающихся в щели, будет равно:

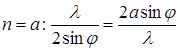Мы видим, что n при постоянных а и l зависит от угла наблюдения j. Чем больше угол наблюдения, тем больше число зон Френеля укладывается в щели.

Следует указать, что когда наблюдение ведется с помощью линзы, то при положении экрана в главном фокусе различным углам j соответствуют отдельные точки экрана. Поэтому мы можем говорить о наблюдении под различными углами, понимая под этим различные точки экрана. Когда n равно целому четному числу (n=2m, где m – целое число), то все зоны можно разбить на n/2 пар; в результате интерференции действие двух соседних зон Френеля равно нулю, а, следовательно, равно нулю и действие всей щели.

Таким образом, под углами j, соответствующими четным n, мы будем наблюдать темноту. Формула, определяющая эти углы, имеет следующий вид:

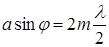где m – целое число.

Когда n равно целому нечетному числу (n=2m+1), то действие щели эквивалентно действию одной зоны Френеля, ибо действие остальных зон взаимно компенсируется. В этом случае мы наблюдаем максимум света.

Формула, определяющая направление максимумов света, имеет следующий вид:

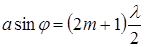Cмысл последних двух формул заключается в следующем: если разность хода между крайними лучами, проходящими сквозь щель, равна четному числу полуволн, то мы наблюдаем темноту; если разность хода между этими лучами равна нечетному числу полуволн, то мы наблюдаем максимум света.

Мы видим, что в пространстве за щелью вместо геометрического силуэта щели получаются полосы, которые легко наблюдать на опыте.

Таким образом, расчет освещенности дифракционной картины свелся к учету интерференции между фиктивными элементарными источниками, заполняющими изучаемое отверстие в непрозрачном экране.

⇐ Предыдущая 123 4 Следующая ⇒