Пример 1.. Функция распределения описывает вероятность того, что случайная величина примет значение, МЕНЬШЕЕ, чемпеременная , «пробегающая» все значения от до . Данная функция изменяется в пределах и не убывает(т. к. «накапливает» вероятности), а также яв

Тема 1.4. Функции случайных величин

Пример 1.

Непрерывная случайная величина 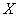задана функцией распределения вероятностей:

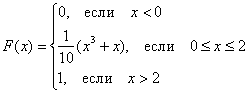
Построить график .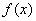

Функция распределения описывает вероятность того, что случайная величина примет значение, МЕНЬШЕЕ, чемпеременная , «пробегающая» все значения от до . Данная функция изменяется в пределах и не убывает(т. к. «накапливает» вероятности), а также является непрерывной (для НСВ).

Очевидно, что случайная величина 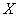принимает случайные значения из отрезка 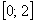, и какие из них более вероятны, а какие – менее, наглядно показывает функция ПЛОТНОСТИ распределения вероятностей

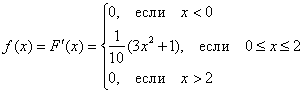
Опорные точки: 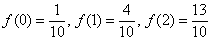с чертежом:

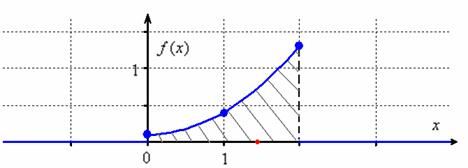
В отличие от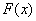 функции плотности может быть разрывна и может принимать значения бОльшие единицы (как в нашем случае); может, как убывать, так и возрастать и даже иметь экстремумы (наша часть параболы растёт). Однако, она неотрицательна: 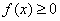и обладает свойством 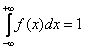, которое лучше всегда проверять. В силу аддитивности интеграла:

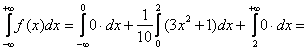
– данный результат равен заштрихованной площадии с вероятностной точки зрения означает тот факт, что случайная величина 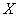достоверно примет одно из значений отрезка 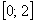. Причём, по чертежу хорошо видно, что значения из правой части отрезка гораздо более вероятны, чем значения слева.

И эти вероятности оцениваются частями площади, а не значениями функции .

Можно вычислить:

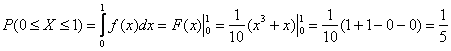– вероятность того, что случайная величина 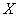примет значение из промежутка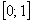

Пример 2. решить самостоятельно Случайная величина X распределена равномерно на отрезке [a,b]. Найдите плотность вероятности случайной величины У = X².

Пример 3. Нормально распределенная случайная величина Х задана своими параметрами – 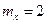– математическое ожидание и 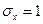– среднее квадратическое отклонение. Требуется написать плотность вероятности и построить ее график, найти вероятность того, Х примет значение из интервала 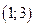, найти вероятность того, что Х отклонится (по модулю) от математического ожидания не более чем на 2.

Плотность распределения определяется по формуле:

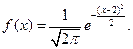
Найдем вероятность попадания случайной величины в интервал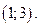

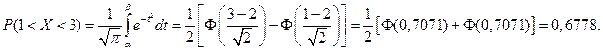
Найдем вероятность отклонение случайной величины от математического ожидания на величину, не большую чем 2:

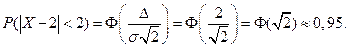
Тот же результат может быть получен с использованием нормированной функции Лапласа:

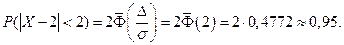
Пример 4.решить самостоятельно Поезд состоит из 100 вагонов. Масса каждого вагона – случайная величина, распределенная по нормальному закону с математическим ожиданием т. и средним квадратичным отклонением 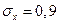т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется.