Хелпикс

Главная

Контакты

Случайная статья



и об их соотношении. Простейший способ решения задачи



 

Тема 10.Принятие решений при отсутствии информации о состоянии внешней среды.

 

План:

 

1.Принцип неизвестного основания Даниила Бернулли.

2. Способ, использующий понятие Байесова множества.

1. ЛПР не располагает никакой информацией о вероятностях появления различных состояний внешней среды ej , в том числе

и об их соотношении. Простейший способ решения задачи

состоит в использовании точечных оценок неизвестного априорного распределения, причем критерии выбора в таких условиях принимают известный «принцип недостаточного основания», предложенный Даниилом Бернулли, и означают, что если нет данных, позволяющих считать одно состояние среды ej Ε бо-

лее вероятным, чем любое другое, то априорные вероятности всех этих состояний следует считать равными p j = 1n .

Оптимальной по критерию Бернулли—Лапласса считается альтернатива, максимизирующая математическое ожидание полезности, т.е.

 

1

 n
 

B( p, x ) = max B( p, xi ) = max(

∑yij ) .
 

n
  i i j=1

Или

Существует несколько критериев для выбора оптимальной стратегии при принятии решения в условиях риска и неопределенности.

Критерий Лапласа: применяется, если можно предполагать, что все варианты внешних условий одинаково вероятны. Для каждого решения находится средняя оценка по всем вариантам внешних условий (средний выигрыш):

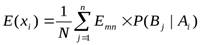
где N– количество состояний внешней среды.

Лучшим является решение с максимальной оценкой.

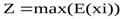
где Z – оптимальная стратегия.

2.  Рассмотрим множество всевозможных распределений вероятностей состояний внешней среды. Так как ∑p j =1, то в каждом j=1  распределении достаточно задать лишь (n −1) вероятность, например, p1, ..., pn−1.

Обозначим p = ( p1, ..., pn−1) . Очевидно, что каждому конкретному распределению вероятностей соответствует точка (n −1) -мерного пространства с координатами p1, ..., pn−1 , лежащая в замкнутой области, определяемой соотношениями:

 

 

n−1

p j ≥ 0, j =1, n −1 , ∑p j ≤1.

j=1

Область, определяемая таким образом, называется (n −1) - мерным симплексом pn−1 . Если n = 2, то одномерный симплекс p1 — это отрезок [0,1], если m = 3, то двумерный симплекс p2 — треугольник.

Если в распоряжении ЛПР имеется m альтернатив, то этот симплекс можно разбить на m непересекающихся подмножеств, таких, что в любой точке этого подмножества оптимальной по критерию Байеса является одна и та же альтернатива.

Такое подмножество (из p ), соответствующее стратегии xi , называется байесовым множеством этой стратегии. Будем обозначать его p (xi ) или pi .

Понятию байесова множества можно дать простую геометрическую интерпретацию.

Если среда может находиться всего в двух состояниях n = 2 с вероятностями p1 и p2 =1− p1 , тосимплекс p1 ( p1 ≥ 0, p1 ≤1) —

есть отрезок.

Математическое ожидание полезности при использовании альтернативы xi

B( p, xi ) = p1 yi1 + (1− p1) yi2 = p1( yi1 − yi2 ) + yi2 .

Таким образом, каждой альтернативе xi соответствует прямая на плоскости с системой координат ( p, B) .

Приведем пример построения байесовых множеств p(xi ) в одномерном симплексе при наличии трех альтернатив (рис. 5.2). Множеству p(xi ) соответствует отрезок симплекса, на котором альтернатива xi обеспечивает максимум математического ожидания полезности.

Можно доказать, что каждое байесово множество образует в (n −1) -мерном пространстве замкнутый выпуклый многогранник (в нашем случае при n = 2 — отрезок, а при n = 3 — многогранник).

Объем многогранника будем рассматривать как меру байесова множества p(xi ) и обозначим ее µ( pi ) . Назовем интегральным потенциалом альтернативы xi величину

∫B( p, xi )dp

π(xi ) = 1−pµi ( pi ) / µ( pm−1) ,

где числитель характеризует интегральное (средневзвешенное по всем априорным распределениям) байесово значение оценочного функционала;

µ( pm−1) — мера (объем) симплекса, и, следовательно, знаменатель определяет геометрическую вероятность непопадания вектора p в байесово множество альтернативы xi .

Естественно предположить, что ЛПР стремится к увеличению числителя при возможно меньшем знаменателе. Отсюда получаем критерий наибольшего интегрального потенциала:

π(x ) = max π(xi ) .

Таким образом, в случае отсутствия информации о вероятностях состоянии среды теория не дает однозначных и матема­тически строгих рекомендации по выбору критериев принятия решений. Это объясняется в большей мере не слабостью теории, а неопределенностью самой ситуации. Единственный ра­зумный выход в подобных случаях - попытаться получить дополнительную информацию, например, путем проведения исследований или экспериментов. В отсутствие дополнительной информации принимаемые решения теоретически недостаточно обоснованы и в значительной мере субъективны. Хотя применение математических методов в играх с природой не дает абсолютно достоверного результата и последний в определенной степени является субъективным (вследствие произвольности выбора критерия принятия решения), оно тем не менее создает некоторое упорядочение имеющихся в распоряжении ЛПР данных: задаются множество состояний природы, альтернативные решения, выигрыши и потери при различных сочетаниях состояния «среда - решение». Такое упорядочение пред­ставлений о проблеме само по себе способствует повышению качества принимаемых решений.
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.