
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Базисный метод
Базисный метод
Для анализа динамики рассчитываются следующие показатели:
Базисный метод Цепной метод
| аБсолютный прирост | DУ = УП – У0 D У = УП – УП -1 |
| ТЕМП РОСТА | Кр = УП *100 Кр = УП *100 У0 УП - 1 |
| ТЕМП ПРИРОСТА | ТПР = DУ * 100 ТПР = DУ * 100 У0 УП – 1 ТПР = ТР – 100 |
| КОЭФФИЦИЕНТ РОСТА | Кр = УП Кр = УП У0 УП - 1 |
| КОЭФФИЦИЕНТ ПРИРОСТА | КПР = КР - 1 |
| АБСОЛЮТНОЕ ЗНАЧЕНИЕ 1% ПРИРОСТА | 1 % прироста = DУ ТПР |
Обозначения: УП – последующий уровень;
У0 – нулевой уровень;
УП – 1 - предыдущий уровень.
Абсолютный прирост характеризует увеличение или уменьшение уровня ряда динамики за определенный период времени, показывает абсолютную скорость роста и выражается в единицах измерения ряда..
Темпы роста (снижения) – это относительные величины, которые могут быть выражены в виде коэффициента (Кр) или в виде процентов (Тр). Базисные и цепные темпы роста находятся во взаимосвязи. Если последовательно перемножать цепные темпы роста, взятые в коэффициентной форме, получится базисный темп роста (последнего периода). Можно преобразовать и базисные темпы роста в цепные. Для этого каждый последующий темп роста нужно разделить на предыдущий базисный темп роста.
Темп прироста (снижения) показывает, на сколько процентов изменились размеры явления за изучаемый период.
Абсолютное значение 1% прироста – показывает какое абсолютное значение скрывается за относительным показателем – 1% прироста.
Пример. Рассчитать показатели ряда динамики базисным и цепным методами.
Товарооборот торгового предприятия составил:
I квартал - 5075,0 тыс.руб.
II квартал - 5130,8 тыс.руб.
III квартал - 5260,4 тыс.руб.
IV квартал - 5390,0 тыс.руб.
Решение.
Примечание. Для решения данного задания необходимо воспользоваться формулами из таблицы в лекции. При расчете показателей базисным методом данные всех последующих кварталов – II, III и IV сравниваются с данными I кв., принимаемого за базис. При расчете цепным методом данные каждого последующего квартала сравниваются с предыдущим. При расчете и базисным и цепным методом, изменения рассчитывают, начиная со II кв., т.к. I квартал не с чем сравнивать.
Результаты расчетов оформлены таблицей.
| Показатели | Базисный метод | Цепной метод | ||||
| II квартал | III квартал | IV квартал | II квартал | III квартал | IV квартал | |
| Абсолютный прирост, тыс.руб. | 55,8 | 185,4 | 55,8 | 129,6 | 129,6 | |
| Темп роста, % | 101,1 | 103,7 | 106,2 | 101,1 | 102,5 | 102,5 |
| Темп прироста, % | 1,1 | 3,7 | 6,2 | 1,1 | 2,5 | 2,5 |
| Коэффициент роста | 1,011 | 1,037 | 1,062 | 1,011 | 1,025 | 1,025 |
| Коэффициент прироста | 0,011 | 0,037 | 0,062 | 0,011 | 0,025 | 0,025 |
| Абсолютное значение 1% прироста, тыс.руб. | 50,7 | 50,1 | 50,8 | 50,7 | 51,8 | 51,8 |
3. Средние динамические показатели, формулы их расчета.
Анализ динамического ряда дополняют расчетом средних показателей.
1. Средний абсолютный уровень ряда динамики находят:
- в интервальном ряду - по средней арифметической простой;
- в моментном ряду – по средней хронологической.
2. Средний абсолютный прирост находят по простой арифметической как сумму абсолютных цепных приростов, деленную на их количество. При этом можно использовать взаимосвязь: сумма цепных абсолютных приростов равна последнему базисному, т.е. общему приросту за весь промежуток времени.
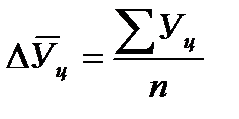 или
или 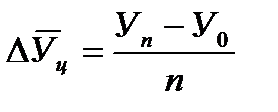 ,
,
где n –количество цепных абсолютных приростов.
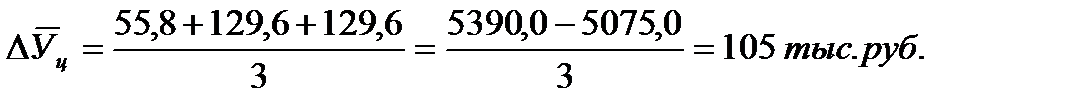
Нужно помнить, что расчетных (аналитических) показателей ряда динамики всегда на один меньше, чем исходных уровней ряда динамики., так как для начального уровня нет базы для сравнения, поэтому начальный уровень часто нумеруется как нулевой, тогда количество расчетных показателей динамики (n) совпадает с порядковым номером последнего исходного уровня ряда, но исходных уровней на 1 больше.
3. При анализе развития явления часто возникает потребность дать обобщающую характеристику интенсивности развития за длительный период. Для этого рассчитывают средние темпы роста и прироста:
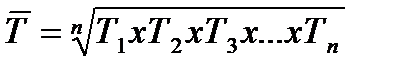 ,
,
где Т – цепные темпы роста, выраженные в форме коэффициента.
n – число темпов роста.
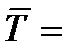
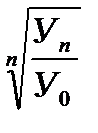 , где У0 – начальный уровень ряда динамики;
, где У0 – начальный уровень ряда динамики;
Уn – конечный уровень ряда динамики;
n - число уровней ряда динамики не считая базисного.
Пример.
Рассчитать возможный объем реализации трикотажных изделий на планируемый год.
Реализация трикотажа за 5 лет составила (тыс.руб.): 4,2; 5,1; 5,6; 5,9; 6,1.
Решение.
1. Темпы роста в коэффициентной форме цепным методом:
 ;
; 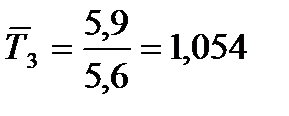
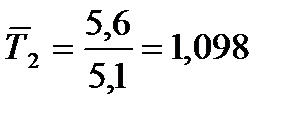 ;
; 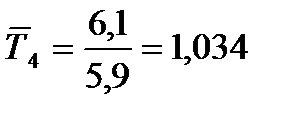
2. Средний темп роста:
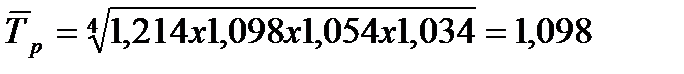 или
или 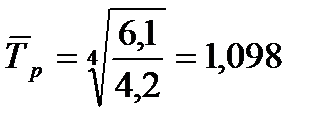
3. Объем реализации на планируемый год 6,1 х 1,098 = 6,7 тыс.руб.
3. Методы анализа основной тенденции развития в рядах динамики.
Одной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления.
Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний.
Для выявления основной тенденции развития явления во времени используются методы:
1. Метод укрупнения интервалов – наиболее простой метод. Основан на укрупнении периодов времени, к которым относятся уровни ряда динамики. Сущность этого метода состоит в том, что данные динамического ряда объединяются в группы по периодам, рассчитывается средний показатель за период (3, 5 лет и т.д.). Такая средняя позволяет выявить направление и характер (ускорение или замедление роста) основной тенденции развития.
2. Метод скользящей средней – сущность метода заключается в том, что рассчитывается средний уровень из определенного числа, обычно нечетного (3,5,7 и т.д.), первых по счету уровней ряда, затем – из такого же числа уровней, но начиная со второго по счету, далее – начиная с третьего и т.д. Таким образом, средняя, как бы «скользит» по ряду динамики, передвигаясь на один срок.
3. Метод аналитического выравнивания – наиболее эффективный и сложный способ выявления основной тенденции. Общая тенденция рассчитывается как функция времени: 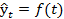 , где
, где 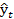 – уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.
– уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.
При сравнении квартальных и месячных данных многих социально-экономических явлений часто обнаруживаются периодические колебания, возникающие под влиянием смены времен года. Они являются результатом влияния природно-климатических условий, общих экономических факторов и других факторов, которые часто регулируются.
К сезонным относят все явления, которые обнаруживают в своем развитии отчетливо выраженную закономерность внутригодовых изменений.
В статистике периодические колебания, которые имеют определенный и постоянный период, равный годовому промежутку носят название «сезонные колебания» или «сезонные волны», а динамический ряд в этом случае называют сезонным рядом динамики.
Сезонные колебания наблюдаются в различных отраслях экономики: производстве сельскохозяйственной продукции, в строительстве, транспорте, торговле и т.д.
Сезонные колебания отрицательно влияют на результаты производственной деятельности, вызывая нарушение ритмичности производства.
В статистике существует ряд методов изучения и измерения сезонных колебаний. Наиболее простой метод – метод сезонной волны.
Метод сезонной волны используется для измерения сезонных колебаний. Для того чтобы выявить устойчивую сезонную волну, на которой не отражались бы случайные условия одного года, индексы сезонности вычисляют по данным за несколько лет (не менее трех), распределенных по месяцам. Для каждого месяца рассчитывается средняя величина уровня, затем вычисляется среднемесячный уровень для всего ряда, после чего определяется показатель сезонной волны – индекс сезонности как процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда: Is = 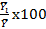 ,
,
где 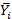 – средний уровень для каждого месяца (минимум за 3 года);
– средний уровень для каждого месяца (минимум за 3 года);
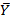 - среднемесячный уровень для всего ряда.
- среднемесячный уровень для всего ряда.
Для наглядного представления сезонной волны, исчисленные индексы сезонности изображают в виде графика.
5. Сущность, значение и классификация индексов.
Для характеристики явлений и процессов экономической жизни статистика широко применяет обобщающие показатели в виде относительных, средних величин, различных коэффициентов. К таким обобщающим показателям относятся и индексы.
Индексы — показатели особого рода. Прежде всего, это относительные величины. От обычных относительных величин их отличает то, что:
- индексы позволяют измерять изменение сложных явлений.
- с помощью индексов можно определить влияние отдельных факторов на изменение динамики сложного явления
- индексы являются показателями сравнений не только с прошлым периодом (сравнение во времени), но и с другой территорией (сравнение в пространстве), а также с нормативами, планами, прогнозами и т.д
Индексом называется относительная величина, характеризующая изменение экономических явлений во времени и в пространстве.
Когда рассматривается сопоставление уровней изучаемого явления во времени, то говорят об индексах динамики, в пространстве — о территориальных индексах.
Индексы классифицируют по следующим признакам:
1. По содержанию изучаемых объектов:
- индексы объемных (количественных) показателей — индексы физического объема промышленной и сельскохозяйственной продукции, физического объема розничного товарооборота, потребления отдельных продуктов и др. При расчете таких индексов количества оцениваются в одинаковых, сопоставимых ценах.
- индексы качественных показателей — индексы цен, себестоимости, производительности труда и др.
2. По степени охвата элементов совокупности:
- индивидуальные индексы - служат для характеристики изменения отдельных элементов сложного явления (например, изменение объёма выпуска телевизоров определенной марки, рост или падение цен на акции в каком-либо акционерном обществе и т.д.)
- общие индексы - отражают изменение всех элементов сложного явления. При этом под сложным явлением понимают такую статистическую совокупность, отдельные элементы которой непосредственно не подлежат суммированию (физический объем продукции, включающий разноименные товары, цены на разные группы продуктов и т.д.).
Если индексы охватывают не все элементы сложного явления, а лишь часть, то их называют групповыми или субиндексами (например, индексы физического объема продукции по отдельным отраслям промышленности: машиностроение или легкая промышленность, в сельском хозяйстве индекс валовой продукции, а субиндекс – индекс продукции растениеводства и животноводства).
3. По методам расчета общих индексов:
- индексы агрегатные (суммарные) – основная форма общих индексов;
- средние из индивидуальных индексов – производные индексы, которые получают в результате преобразования агрегатных индексов.
4. В зависимости от базы сравнения:
- цепные индексы;
- базисные индексы.
6. Формы и виды индексов.
В индексах, характеризующих изменение явления в динамике, различают два периода:
- базисный – это начальный период, т.е. период с которым производится сравнение;
- отчетный (текущий) - период, уровень которого сравнивается.
Индивидуальными индексами называются относительные числа, характеризующие соотношение отдельных величин несложных экономических явлений.
Для расчета индивидуальных индексов (i) применяются следующие формулы:
- индивидуальный индекс цены 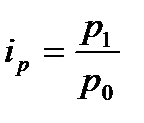 , где
, где
- р0 – цена за единицу продукции в базисном периоде;
- р1 - цена за единицу продукции в отчетном периоде.
- индивидуальный индекс физического объема (количества) 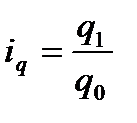 , где
, где
- q0 - количество реализованных товаров в базисном периоде;
- q1 - количество реализованных товаров в отчетном периоде.
- индивидуальный индекс товарооборота 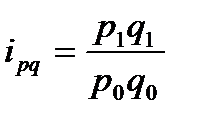 , где
, где
- p1q1 -товарооборот базисного периода;
- p0q0 - товарооборот отчетного периода.
Общими индексами называются относительные числа, характеризующие соотношения между такими совокупностями величин экономических явлений, которые непосредственно в своей натуральной форме несоизмеримы.
Общие индексы могут быть построены двумя способами: как агрегатные и как средние из индивидуальных, которые в свою очередь делятся на средние арифметические и средние гармонические.
Основной формой общих индексов является агрегатная.
Для преодоления несоизмеримости разных элементов при построении общих индексов, надо ввести в индекс дополнительный показатель, который тесно связан с индексируемой величиной. Такой показатель называется соизмерителем.
Каждый сводный индекс состоит из двух элементов:
1. Индексируемая величина – это величина, которая изучается в данном индексе.
2. Веса индекса – это соизмерители, при помощи которых несоизмеримые показатели индекса приводятся в сопоставимый вид. Веса – это одинаковые величины в числителе и знаменателе индекса.
Общие индексы бывают:
Общий индекс цены 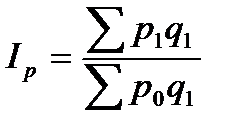
Общий индекс физического объема товарооборота 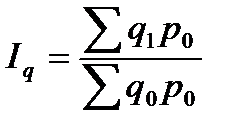
Общий индекс стоимостного объема товарооборота 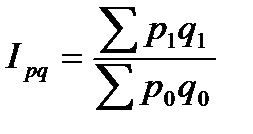 ,
,
где p0q0 - товарооборот базисного периода
p1q1 – товарооборот отчетного периода
p0q1 – товарооборот отчетного периода в сопоставимых ценах.
Для определения агрегатных индексов необходимо иметь абсолютные значения индексированной величины и величины, с помощью которой достигается сравнение уровней явлений, отдельные элементы которых непосредственно не суммируются, т.е. весов индексов и их соизмерителей. Однако не всегда такие показатели есть в отчетности. Если имеющаяся в распоряжении информация не позволяет рассчитать общий агрегатный индекс, используются способ расчета индексов как средних из соответствующих индивидуальных индексов на основе преобразования агрегатных индексов. Для этого используются две формы средних: средняя арифметическая и средняя гармоническая.
Если имеются данные о сумме товарооборота базисного периода по каждой группе товаров и об изменении количества продажи по каждой группе рассчитывается средний арифметический индекс.
Для преобразования используется формула индивидуального индекса физического объема товарооборота 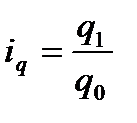 , из которого следует
, из которого следует 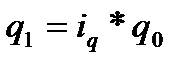
В числителе агрегатного индекса количества заменятся q1 на iqхq0 и формула приобретает следующий вид 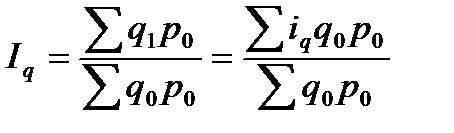
В таком виде индекс объема продукции выступает как средняя арифметическая величина из индивидуальных индексов, взвешенных по стоимости товарооборота базисного периода в базисных ценах (q0 p0).
Чтобы средний арифметический индекс был тождественен агрегатному, весами индивидуальных индексов в нем должны быть взяты слагаемые знаменателя исходного агрегатного индекса.
Агрегатный индекс может быть преобразован не только в средний арифметический, но и в средний гармонический индекс.
Для преобразования используется формула индивидуального индекса цен 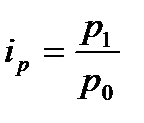 , отсюда
, отсюда 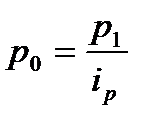 .
.
В агрегатном индексе цен числитель индекса остается без изменения, а в знаменателе р0 заменяется. Формула индекса цен принимает вид:
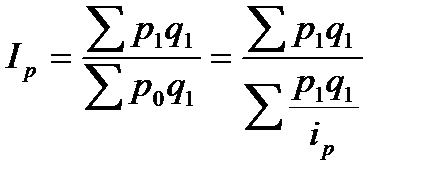
В таком виде индекс цен выступает как средняя гармоническая величина из индивидуальных индексов цен, взвешенных по сумме фактического товарооборота отчетного периода (p1q1).
Чтобы средний гармонический индекс был тождественен агрегатному, весами индивидуальных индексов в нем должны быть взяты слагаемые числителя исходного агрегатного индекса.
7. Использование индексов в анализе динамики.
В экономическом анализе динамики явлений возникает необходимость вычислить индексы не за два, а за несколько последовательных периодов. Поэтому при расчетах получается не один, а несколько индексов. В этих случаях индексы рассчитываются двумя способами.
1. Базисный – каждый последующий период сравнивают с первоначальным периодом, который принимается за базу сравнения (базисный индекс).
2. Цепной – каждый последующий период сравнивается с предыдущим периодом (цепной индекс).
Базисные и цепные индексы могут быть индивидуальные и общие.
Между базисными и цепными индексами (индивидуальными и общими агрегатными) существует взаимосвязь, позволяющая переходить от одних индексов к другим:
- частное от деления последующего базисного индекса на непосредственно предшествующий ему базисный индекс равно цепному индексу
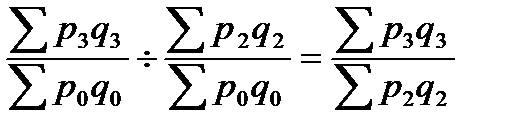
- произведение ряда цепных индексов равно соответствующему базисному индексу
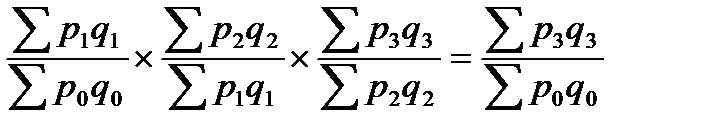
8. Порядок определения влияния отдельных факторов индексным методом.
Индексный метод широко используется для анализа роли отдельных факторов в динамике сложного экономического явления.
Для этого строятся факторные модели типа x=ab, где х – результативный признак, а и b – показатели-факторы.
Индексная система позволяет на её основе выявить влияние отдельных факторов на изменение результативного показателя.
Примером такой модели является взаимосвязь объема товарооборота как результативного признака от уровня цен и физического объема товарооборота. Между индексами существует такая же взаимосвязь, как и между показателями, которые они характеризуют.
Ipq = Ip x Iq - формула взаимосвязи индексов
Взаимосвязь индексов можно использовать для проверки рассчитанных индексов.
Построение индексов 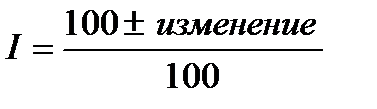
Пример.
Товарооборот торгового предприятия увеличился на 25%, а количество проданных товаров снизилось на 7%. Определить как изменились цены на реализованные товары.
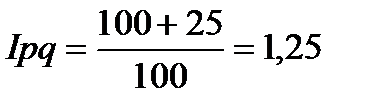 ;
; 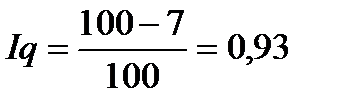 ;
;
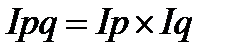
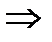
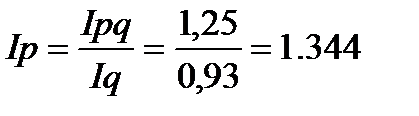 или 134,4%
или 134,4%
Цены на реализуемые товары выросли на 34,4%
С помощью индексов можно рассчитать не только относительные показатели влияния факторов на результативный показатель, но и абсолютные:
- общее изменение товарооборота в фактических ценах 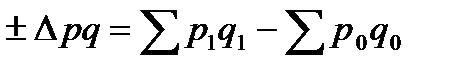
в том числе за счет изменения: - цены 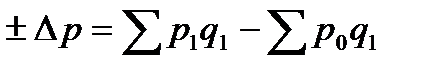
- количества 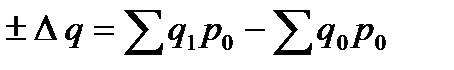
Пример.
Рассчитать индивидуальные и общие индексы цены, физического объема и стоимостного объема товарооборота, показать взаимосвязь индексов.
Решение.
Примечание. Результаты расчетов оформляем в таблице. В таблице обычным шрифтом выделены исходные данные, а курсивом – результаты расчетов. Также, в таблице представлен алгоритм расчета показателей по графам. Методика определения общих индексов и определения влияния факторов дана под таблицей. Индексы рассчитываются с точностью до 0,001.
| Товар | Базисный период | Отчетный период | Индивидуальные индексы | Товарооборот, тыс.руб. | ||||||
| Продано, кг q0 | Цена за кг,руб . p0 | Продано, кг q1 | Цена за кг, руб. p1 | Цены ip | Количества iq | Товарооборота, ipq | базисный p0q0 | отчетный p1q1 | Отчетный в сопоставимых ценах p0q1 | |
| 6=5/3 | 7=4/2 | 8=6х7 | 9=2х3 | 10=4х5 | 11=3х4 | |||||
| А | 50,0 | 55,0 | 1,1 | 1,091 | 1,2 | 13750 | 16500 | 15000 | ||
| Б | 80,0 | 1,25 | 0,9 | 1,125 | 40000 | 45000 | 36000 | |||
| Итого | - | - | - | - | - | - | - | 53750 | 61500 | 51000 |
1. Общий индекс стоимостного объема товарооборота
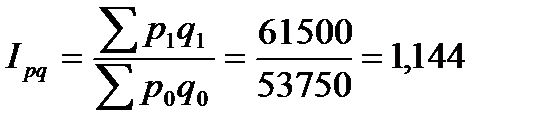 или 114,4% товарооборот вырос на 14,4%
или 114,4% товарооборот вырос на 14,4%
2. Общий индекс цены
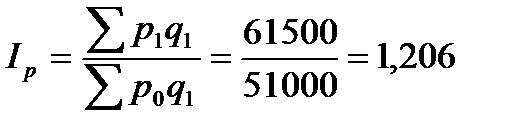 или 120,6% цены увеличились на 20,6%
или 120,6% цены увеличились на 20,6%
3. Общий индекс физического объема товарооборота
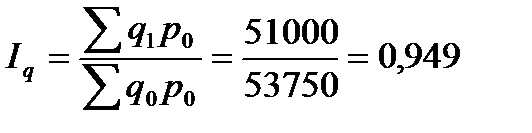 или 94,9% количество проданных товаров снизилось на 5,1%
или 94,9% количество проданных товаров снизилось на 5,1%
4. Взаимосвязь индексов Ipq = Ip x Iq = 1,206 х 0,949 = 1,144
5. Общее изменение товарооборота в фактических ценах
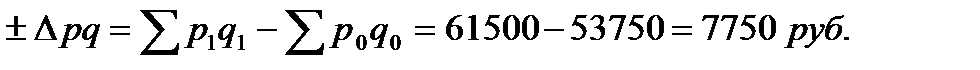
в том числе за счет изменения:
- цены 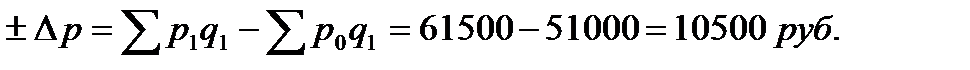
- количества 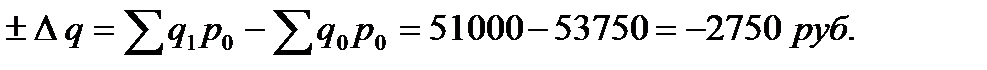
Баланс факторов 10500 + (-2750) = 7750 руб.
6. Расчет средних индексов:
-среднегармонический индекс цен
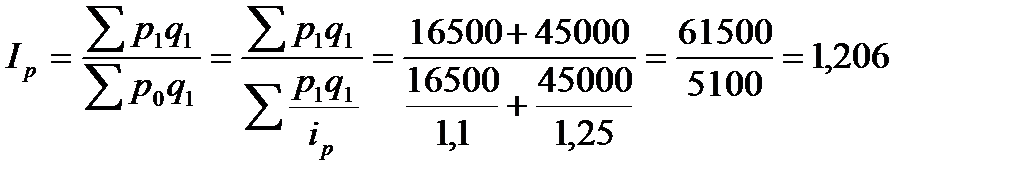
- среднеарифметический индекс количества
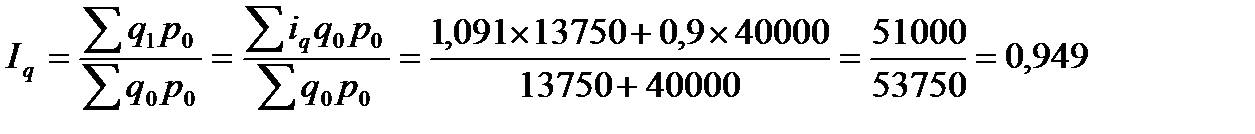
Литература.
Статистика [Текст]: учебник для студентов учреждений СПО / В. С. Мхитарян, Т. А. Дуброва, В. Г. Минашкин; ред. В. С. Мхитарян. – 14-е изд., стер. – М.: Академия, 2015, (с.215-258, 131-143).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|