
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Значения тригонометрических функций
Тема: Основные тригонометрические операции
План занятия:
1. Понятие тригонометрических операций
2. Операции нахождения синуса, косинуса, тангенса и котангенса угла.
Вопрос 1.Понятие тригонометрических операций
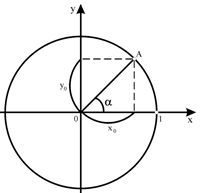 Рассмотрим окружность радиуса R = 1 с центром в начале координат, уравнение которой: x2 + y2 = 1.
Рассмотрим окружность радиуса R = 1 с центром в начале координат, уравнение которой: x2 + y2 = 1.
Пусть А– произвольная точка этой окружности, (x0, y0) – ее координаты, α – величина угла, образованного отрезком ОАс положительной полуосью Ох.
Иначе говоря, определение координат точек единичной окружности и обратное действие называются тригонометрическими операциями.
Вопрос 2.Операции нахождения синуса, косинуса, тангенса и котангенса угла.
Тригонометрические функции синус и косинус определяются формулами: sin α = y0 , cos α = x0
Т.е. синус угла α равен вертикальной координате y0 точки А, а косинус угла α равен горизонтальной координате x0 точки А.
Эти определения согласуются с определениями синуса и косинуса в прямоугольном треугольнике: синус угла α равен отношению противолежащего катета y0 к гипотенузе, равной 1, а косинус угла α равен отношению прилежащего катета x0 к гипотенузе, равной 1.
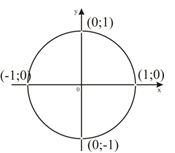 Найдём значения синуса и косинуса углов, соответствующих точкам, лежащих на координатных осях.
Найдём значения синуса и косинуса углов, соответствующих точкам, лежащих на координатных осях.
У точки, соответствующей углу 0°, координаты (1; 0), т.е. х0 = 1, у0 = 0.
Это означает, что sin 0° = 0, cos 0° = 1
У точки, соответствующей углу 90°, координаты (0; 1), т.е. х0 = 0, у0 = 1.
Это означает, что sin 90° = 1, cos 90° = 0
У точки, соответствующей углу 180°, координаты (–1; 0), т.е. х0 = –1, у0 = 0.
Это означает, что sin 180° = 0, cos 180° = -1
У точки, соответствующей углу 270°, координаты (0; –1), т.е. х0= 0, у0 = –1.
Это означает, что sin 270° = -1, cos 270° = 0
Дополнительными тригонометрическими операциями являются тангенс и котангенс
tg (x) = 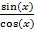 ctg (x) =
ctg (x) = 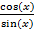
Значения тригонометрических функций
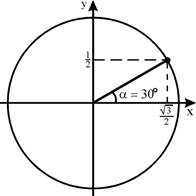 1)
1) 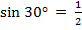 , cos 30° =
, cos 30° = 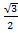
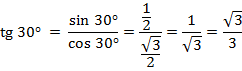
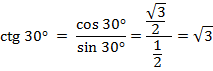
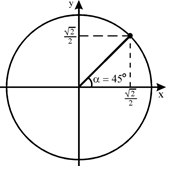 2)
2) 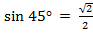 ,
, 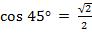
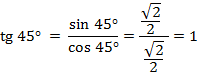
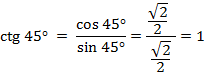
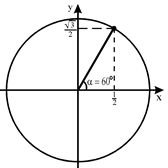 3)
3) 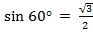 ,
, 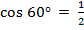
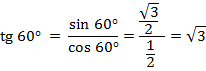
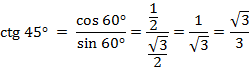
Аналогичные рассуждения можно провести для углов 120°, 135°, 150°, находящихся во второй четверти.
Найдём значения тригонометрических функций угла 150°. Этот угол соответствует углу 30° из первой четверти.
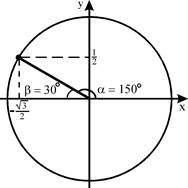
 АОХ =
АОХ =  ,
,  ВОХ = 150°
ВОХ = 150°
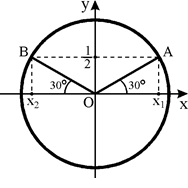 По чертежу видно, что у точек А и В координата у одинаковая и равна
По чертежу видно, что у точек А и В координата у одинаковая и равна 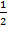 ,
,
т.е. sin 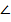 АОХ = sin
АОХ = sin 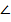 ВОХ =
ВОХ = 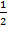
А что же cos 150º? Это координата х точки В. Мы видим, что равны отрезки ОХ1 и ОХ2. Значит, координата х точки В по модулю такая же, как у точки А. Но т.к. В лежит слева от нуля, то координата х имеет знак «–».
Итак, если 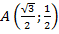 , то
, то 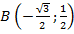
И тогда sin 150º = sin 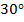 =
= 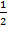 , cos 150º = - cos
, cos 150º = - cos 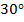 =
= 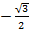 ,
,
tg 150º = - tg 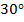 =
= 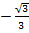 , ctg 150º = - ctg
, ctg 150º = - ctg 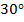 =
= 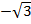
Значения тригонометрических функций для некоторых значений аргумента
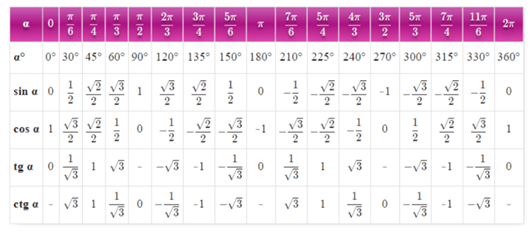
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|