Примеры многогранников. Основные элементы многогранников

Тема:Многогранник и его элементы. Призма

План занятия:

1. Многогранник и его элементы.

2. Призма. Прямая и правильная призмы.

3. Площадь боковой и полной поверхностей призмы

Вопрос 1. Многогранник и его элементы.

Определение многогранника. Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть многогранной поверхностью или многогранником.

Примеры многогранников

Рассмотрим следующие примеры многогранников:

1. Тетраэдр ABCD – это поверхность, составленная из четырех треугольников: АВС, ADB, BDC и ADC (рис. 1).

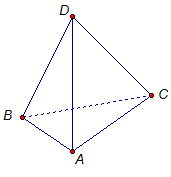
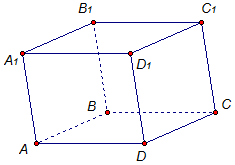
Рис. 1 Рис. 2

2. Параллелепипед ABCDA₁B₁C₁D₁ – это поверхность, составленная из шести параллелограммов (рис. 2).

Основные элементы многогранников

Основными элементами многогранника являются грани, ребра, вершины.

Грани – это многоугольники, составляющие многогранник.

Ребра – это стороны граней.

Вершины – это концы ребер.

Рассмотрим тетраэдр ABCD (рис. 1). Укажем его основные элементы.

Грани: треугольники АВС, ADB, BDC, ADC.

Ребра: АВ, АС, ВС, DC, AD, BD.

Вершины: А, В, С, D.

Рассмотрим параллелепипед ABCDA₁B₁C₁D₁(рис. 2).

Грани: параллелограммы АА₁D₁D, D₁DСС₁, ВВ₁С₁С, АА₁В₁В, ABCD, A₁B₁C₁D₁.

Ребра: АА₁, ВВ₁, СС₁, DD₁, AD, A₁D₁, B₁C₁, BC, AB, A₁B₁, D₁C₁, DC.

Вершины: A, B, C, D, A₁,B₁,C₁,D₁.

Вопрос 2. Призма. Прямая и правильная призмы.

Призма – это многогранник, в основаниях которого лежат равные многоугольники, а боковые грани – параллелограммы.

Основания призмы – это две грани, являющиеся равными многоугольниками, которые лежат в параллельных плоскостях.

Боковыми гранями являются все грани призмы, кроме оснований. Каждая боковая грань является параллелограммом.

Общие стороны боковых граней называются боковыми ребрами.

Вернемся к рисунку 1. В пятиугольнике ABCDFA₁B₁C₁D₁F₁:

ABCDF и A₁B₁C₁D₁F₁ – основания призмы.

Боковыми гранями являются грани АА₁В₁В, ВВ₁С₁С, CC₁D₁D, DD₁F₁F, FF₁A₁A. А боковыми ребрами – АА₁, ВВ₁, СС₁, DD₁, FF₁.

12 Следующая ⇒