Хелпикс

Главная

Контакты

Случайная статья



Задачи для самостоятельного решения.



Задачи для самостоятельного решения.

1. Известна высота h и радиус r цилиндра. Найти его объем.

2. Пусть известны координаты вершин треугольника X1,Y1; X2,Y2; X3,Y3. Найти: периметр треугольника P и его площадь S. Треугольник лежит на длинной стороне (D).

3. Пусть некоторый процесс начался в H1 часов, Min1 минут, а закончился, когда было H2 часов и Min2 минут. Вычислить длительность этого процесса (в часах HD и минутах MinD). Считаем, что процесс идет внутри одних суток.

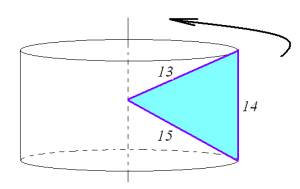
4. Найдите объем и площадь поверхности тела, полученного при вращении треугольника со сторонами 13, 14 и 15 вокруг прямой, проходящей через вершину среднего по величине угла треугольника параллельно средней его стороне.

Чтобы лучше представить себе, как может выглядеть подобная фигура, рассмотрим чертеж:

 

 

5. Вычислите углы параллелограмма, если его углы, прилежащие к одной стороне, относятся как 2 : 3.

Д а н о: ABCD – параллелограмм; угол A: угол B = 2 : 3.

Н а й т и:  угол A; угол B; угол C; угол D.

 

6. Периметр параллелограмма равен 122 см. Одна из его сторон больше другой на 25 см. Найти стороны параллелограмма.

Д а н о: ABCD – параллелограмм; ВС – АВ = 25 см; PАВСD = 122 см.

Н а й т и: АВ; ВС; CD; AD.

 

 

7. Биссектриса угла А прямоугольника ABCD делит сторону ВС на части 2 см и 6 см. Найдите периметр прямоугольника.

Д а н о: ABCD – прямоугольник; АЕ – биссектриса A; BE = 2 см; ЕС = 6 см; (или BE = 6 см, ЕС = 2 см).

Н а й т и: PАВСD.
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.