Задача №2

Задача №2

КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

1. Колесо вращается с постоянным угловым ускорением 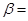2 рад/c². Через t=0,5 с после начала движения полное ускорение колеса стало равным а=0,136 м/c². Найти радиус колеса R.

2. Найти во сколько раз нормальное ускорение точки 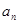, лежащей на ободе вращающегося колеса, больше ее тангенциального ускорения 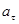для того момента, когда вектор полного ускорения этой точки 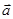составляет угол 30⁰ с вектором ее линейной скорости .

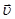3. Колесо радиуса r=0,1 м вращается с постоянным угловым ускорением 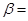3,14 рад/с². Найти для точек на ободе колеса к концу первой секунды после начала движения:

1) угловую скорость 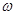, 2) линейную скорость 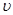, 3) тангенциальное ускорение 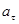, 4) нормальное ускорение 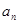, 5) полное ускорение a, 6) угол 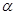между вектором полного 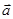и нормального 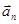ускорений.

4. Найти угловое ускорение колеса 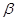, если известно, что через t=2 с после начала равноускоренного движения вектор полного ускорения 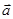точки, лежащей на ободе, составляет угол 60⁰ с направлением линейной скорости 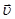этой точки.

5. Точка движется по окружности радиуса r=0,2 м с постоянным тангенциальным ускорением 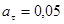м/c². Через сколько времени t после начала движения нормальное ускорение точки 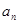будет:

1) равно тангенциальному ;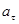

2) будет вдвое больше тангенциального ?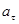

6. Колесо вращается с постоянным угловым ускорением 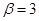рад/c². Определить радиус колеса, если через t = 1 с после начала движения полное ускорение равно 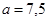м/c² .

7. Маховик, задерживаемый тормозом, за некоторое время t поворачивается на угол 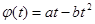(а =4 рад/c, b=0,3 рад/c²). Определить:

1) угловую скорость 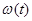вращения маховика в момент времени t =2 с;

2) в какой момент времени t₁ вращение маховика прекратится;

3) чему равны по величине полное a, тангенциальное 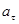и нормальное 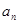ускорения, если радиус окружности маховика R=0,1 м?

8. Точка движется по окружности радиусом R = 1,2 м. Уравнение движения точки 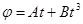, где A = 0,5 рад/c, В = 0,2 рад/c² . Определить тангенциальное 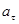, нормальное 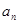и полное a ускорения точки в момент времени t = 4 c.

9. Маховик, вращавшийся с постоянной частотой 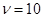с^-1, при торможении начал вращаться равнозамедленно. Когда торможение прекратилось, вращение маховика снова стало равномерным, но уже с частотой 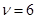с^-1. Определить угловое ускорение 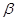маховика и продолжительность t торможения, если за время равнозамедленного движения маховик сделал N=50 оборотов.

10. Определить линейную скорость v и нормальное ускорение 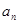точек, лежащих на земной поверхности: 1) на экваторе; 2) на широте Москвы ( 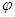=56°).

11. Линейная скорость v₁ точек на окружности вращающегося диска равна 3 м/с. Точки, расположенные на 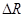= 10 см ближе к оси, имеют линейную скорость v₂=2 м/с. Определить частоту вращения 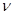диска.

12. Диск радиусом 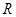=10 см, находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением 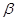=0,5 рад/с². Найти тангенциальное 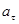, нормальное 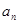и полное а ускорения точек на окружности диска в конце второй секунды после начала

вращения.

13. Диск радиусом R=20 см вращается согласно уравнению 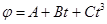, где A=3 рад, 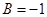рад/с, С=0,1 рад/с³. Определить тангенциальное 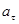, нормальное 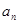и полное а ускорения точек на окружности диска для момента времени t=10 с.

14. Маховик начал вращаться равноускоренно и за промежуток времени 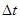=10 с достиг частоты вращения v=300 мин^-1. Определить угловое ускорение 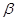маховика и число N оборотов, которое он сделал за это время.

15. Велосипедное колесо вращается с частотой v= 5 c^-1. Под действием сил трения оно остановилось через интервал времени 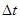=1 мин. Определить угловое ускорение 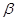и число N оборотов, которое сделает колесо за это время.

16. Колесо автомашины вращается равноускоренно. Сделав N=50 полных оборотов, оно изменило частоту вращения от 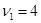c^-1 до 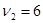с^-1. Определить угловое ускорение 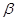колеса.

17. Диск вращается с угловым ускорением 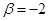рад/с². Сколько оборотов N сделает диск при изменении частоты вращения от 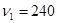мин^-1 до 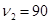мин^-1. Найти время 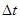, в течение которого это произойдет.

18. Точка движется равномерно по окружности радиусом R=30 см с постоянным ускорением 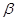. Определить тангенциальное ускорение а_τ точки, если известно, что за время t=4 c она совершила три оборота и в конце третьего оборота её нормальное ускорение а_n=2,7 м/с².

19. Точка движется по окружности радиусом R=10 см с постоянным тангенциальным ускорением а_τ. Найти тангенциальное ускорение а_τ точки, если известно, что к концу пятого оборота после начала движения линейная скорость точки v=79,2 см/с.

20. В первом приближении можно считать, что электрон в атоме водорода движется по круговой орбите с линейной скоростью v. Найти угловую скорость 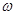вращения электрона вокруг ядра и его нормальное ускорение а_п. Считать радиус орбиты 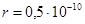м и линейную скорость электрона на этой орбите v 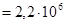м/с.

21. Точка движется до окружности радиусом R =2 см. Зависимость пути от времени дается уравнением 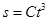, где 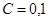см/с³. Найти нормальное а_п и тангенциальное а_τ ускорения точки в момент, когда линейная скорость точки v =0,3 м/с.

22. Точка движется по окружности так, что зависимость пути от времени дается уравнением 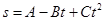, где В=2 м/с и С=1 м/с². Найти линейную скорость v точки, ее тангенциальное а_τ, нормальное а_п и полное а ускорения через время t=3 с после начала движения, если известно, что при t¢ =2 с нормальное ускорение точки а¢_п = 0,5 м/с².

23. Колесо радиусом R = 10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе колеса, от времени дается уравнением v=At+Bt², где A=3 см/с² и В=1 см/с³. Найти угол 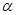, составляемый вектором полного ускорения a с радиусом колеса в моменты времени t, равные: 0, 1, 2, 3, 4 и 5 с после начала движения.

24. Колесо вращается, так, что зависимость угла поворота радиуса колеса, от времени дается уравнением 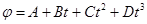, где B=1 рад/с, С=1 рад/с² и D=1 рад/с³. Найти радиус R колеса, если известно, что к концу второй секунды движения для точек, лежащих на ободе колеса, нормальное ускорение а_п =346 м/с².

25. Материальная точка движется по окружности радиусом 1 м без начальной скорости. Ее угловое ускорение зависит от времени по закону 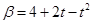. Найти линейную скорость и нормальное ускорение через 3 с после начала движения.

26. Зависимость угловой скорости от времени для материальной точки, движущейся по окружности радиусом 2 м, дается равенством 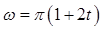. Определить для момента времени t = 5 c число оборотов, совершенных точкой, и ее угловое ускорение.

27. Материальная точка движется по окружности радиусом 1 м. Зависимость ее угла поворота от времени дается равенством 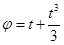. Найти для момента времени t = 2 c линейную и угловую скорости, а также нормальное, тангенциальное и полное ускорения точки.

28. Нормальное ускорение материальной точки, движущейся по окружности радиусом 1 м, меняется по закону 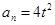. Определить скорость точки в момент времени t = 2 c и путь, пройденный точкой за первые 3 с.

29. Материальная точка движется по окружности радиусом 3 м. При этом зависимость ее линейной скорости от времени имеет вид 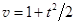. Определить ускорение точки в момент времени t = 2 c и путь, пройденный точкой за первые 2 с.

30. Точка движется по окружности радиусом R =2 см. Зависимость пути от времени дается уравнением 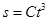, где 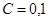см/с³. Найти нормальное 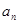и тангенциальное 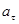ускорения точки в момент, когда линейная скорость точки 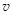= 0,3 м/с.