
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение тригонометрических уравнений вида ctg x = а.
Решение тригонометрических уравнений вида ctg x = а.
Определение: Арккотангенсом числа а 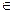 R называется такое число х
R называется такое число х 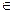 (0;
(0; 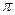 ), котангенс которого равен а:
), котангенс которого равен а:
arcctg а = х, если ctg х = а и 0 < х < 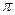
 .
.
Вывод: Все корни уравнения ctg x = а, где а 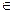 R, можно находить по формуле:
R, можно находить по формуле:
х = arcctg а + pк,гдек Z
| Частные случаи уравнения: | Формулы корней: |
| ctg х = 0 | х = 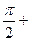 πn πк, где к πn πк, где к 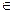 Z Z
|
Например:Решите уравнение 3 ctg х = - 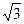
ctg х = - 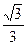
По формуле х = arcctg а + pк, гдек 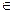 Z находим корни уравнения:
Z находим корни уравнения:
х = arcctg (- 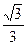 )+ pк =
)+ pк = 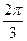 + pк, где к
+ pк, где к 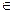 Z
Z
Задания для самостоятельного выполнения
№1.Вычислить:
1) arcctg 1 2) arcctg 0 3) arcctg (- 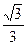 )
)
4) arcctg (-1) 5) arcctg 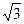
№2. Вычислить значение выражения:
1) 6 arctg 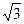 + 3 arcctg (-
+ 3 arcctg (- 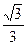 ) 2) 4 arcctg 1 + 12 arcsin
) 2) 4 arcctg 1 + 12 arcsin 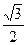
3)12 arcsin 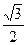 - 3 arcctg
- 3 arcctg 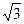 4) 4 arccos (-
4) 4 arccos (- 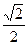 ) + 8 arcctg 1
) + 8 arcctg 1
№3. Решите уравнение:
1) сtg х = - 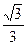 2) сtg х = 0 3) 3сtg х =
2) сtg х = 0 3) 3сtg х = 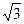
4) сtg 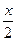 = -1 5) ctg (х +
= -1 5) ctg (х + 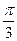 ) = 0 6) 1 + ctg ( 2х -
) = 0 6) 1 + ctg ( 2х - 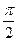 ) = 1
) = 1
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|