Задачи по курсу. Фундаментальные основы квантовой радиофизики (2020)

Задачи по курсу

"Фундаментальные основы квантовой радиофизики" (2020)

1. Найти функцию отклика классического гармонического осциллятора с затуханием 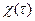на внешний импульс электромагнитного поля .

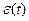2. Электрон находится в бесконечно глубокой прямоугольной потенциальной яме в основном состоянии. Определить (в первом порядке теории возмущений) вероятность перехода за импульс в первое возбужденное состояние под действием лазерного импульса гауссовой формы 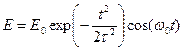. Считать, что , .

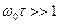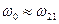3. Электрон находится в гармоническом потенциале с частотой 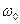. Определить средний по квантовому состоянию дипольный момент системы в электромагнитном поле с частотой 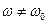. Сравнить результаты квантового и классического решения задачи в случае мгновенного включения поля.

4. Сравнить вероятности двухфотонных переходов 1s--> 3s и 1s--> 3d в атоме водорода в линейно поляризованном поле с частотой .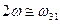

5. В низшем порядке теории возмущений оценить квадратичную нелинейную поляризуемость атомарного водорода в оптическом диапазоне частот.

6. Показать, что для квантовой системы с центрально-симметричным потенциалом (атом) квадратичная восприимчивость равна нулю.

7. В приближении двухуровневой системы (энергии Е₁ и Е₂ и соответствующие им волновые функции j₁ и j₂ считать известными) определить динамику населенностей состояний в резонансном электромагнитном поле 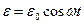( 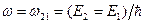). В начальный момент времени ( 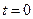) система находится в состоянии 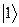. Определить среднее по квантовому состоянию значение дипольного момента как функцию времени.

8. Определить естественную ширину L_a линии в водородоподобном ионе с зарядом Z.

9. Длина волны перехода между компонентами сверхтонкой структуры основного состояния атома водорода 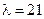см. Оценить время спонтанного перехода.

10. В рамках классической электродинамики определить форму и ширину спектральной линии, излучаемой атомом (гармоническим осциллятором с частотой ).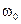

11. Для данного среднего числа квантов в полевой моде определить дисперсию числа квантов в когерентном состоянии и состоянии «сжатого вакуума».

12. Атом (гармонический осциллятор) находится в микрополости, причем частота полевой моды совпадает с частотой атомного перехода. В начальный момент времени атом находится в нижнем возбужденном, а поле – в вакуумном состоянии. Определить вероятность обнаружить атом в возбужденном состоянии как функцию времени.

Литература

1) Атомная физика (Попов-Тихонова), гл.6.12,13,14

2) Физическая оптика (Ахманов-Никитин) лекции 7, 8,18