В таблице «Варианты ответов» оставьте только правильный , остальные удалите.

!!! В таблице «Варианты ответов» оставьте только правильный , остальные удалите.

Обобщение темы

«Формулы сокращённого умножения. Преобразование целых выражений».

I тема. Разность квадратов .

1. а) Выполнить умножение: (3 + х)(3 – х)(9 + х²)

б) Вычислить: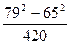

Варианты ответов:

1) х⁴– 81 2) 48	1) 81 – х⁴ 2) 4,8	3) 81 + х⁴ 4) 480

2. а) Выполнить умножение: (a – 1)(a² + 1)(a + 1)

б) Вычислить: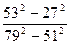

Варианты ответов:

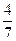
1) а⁴– 1 2)	1) 1 – а⁴ 2) 0,57	1) а⁴ + 1 2) 1,75

3. а) Выполнить умножение: (a – 2)(a² + 4)(a + 2)

б) Вычислить: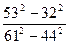

Варианты ответов:

1) а⁴+ 16 2) 10	1) 16 – а⁴ 2) 5	3) а⁴– 16 4) 1

4. а) Выполнить умножение: (y – 3)(y² + 9)(y + 3)

б) Вычислить: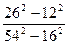

Варианты ответов:

1) у⁴+ 81 2) 2	1) у⁴ – 81 2) 0,2	3) 81 – у⁴ 4) 5

5. а) Выполнить умножение: (x – y)(x + y)( x² + y²)

б) Вычислить: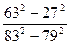

Варианты ответов:

1) у⁴+ 81 2) 1,8	1) у⁴ – 81 2) 5	3) х⁴ – у⁴ 2)

6. а) Выполнить умножение: (b – 2)(b + 2)( b² + 4)

б) Вычислить: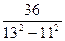

Варианты ответов:

1) b⁴+ 16 2) 0,25	1) b⁴ – 16 2) 0,75	3) 16 – b⁴ 2) 0,5

II тема. Квадрат разности и суммы .

Впишите вместо знака 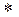какой-нибудь одночлен так, чтобы получилось тождество:

1. ( 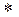+ 2b)² = a² + 4ab +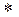

A. a; 4b²; B. 4a²; b; C. 2a; b

2. (3x + 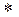)² = 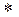+ 6ax + a²

A. 2a; 3х²; B. а; 3х²; C. a; 9х²

3. ( 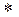– 2m)² = 100 – 40m +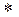

A. 10; 4m²; B. 10; 4m; C. 10; 2m²

4. ( 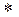– 9c)² = 36a⁴ – 108a²c +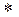

A. 6a; 81с²; B. 18a²; 81с; C. 6а²; 81с²

5. (3b + 2a)² = 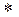+ 12ab +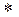

A. 3b²; 2a²; B. 9b²; 4a²; C. 3b²; 4a²

6. (3x + 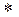)² = 9x² + 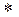+ 49y²

A. 7у; 21ху; B. 7х; 21ху; C. 7у; 42ху

III тема. Разложение многочлена на множители способом группировки .

1.    x² + ax – a²y – axy

A. (х + а)(х – ау)

B. (х – а)(х + ау)

C.   (х +а)(х – у)

2.    a²n + x² – anx – ax

A. (а – х)(аn + х)

B. (а – п)(х + ап)

C. (а – х)(ап – х)

3. 8ax + 16ay – 3bx – 6by

A. (х + 2а)(8a – 3у)

B. (х + 2у)(8a – 3b)

C. (х – 2y)(8a + 3b)

4. 8a³c + 16a² – 6bc – 3abc²

A. (ac – 2)(8a² + 3bc)

B. (ac + 2)(8a² – 3bc)

C. (2 – ac)(8a² – 3bc)

5. 21a + 8xy³ – 24y² – 7axy

A. (3 + хy)(7a – 8у²)

B. (7 + 8у)(3a – ху²)

C. (3 – хy)(7a – 8у²)

6. 14am + 7an – 8bm – 4bn

A. (7а – 4b)(2m + n)

B. (7a + 4b)(2m – n)

C. (2m – n)(7a – 4b)

IVтема. Решение уравнений .

1. (6x – 1)(6x +1) – 4x (9x +2) = – 2

A	B	C	D
	– 8	0,125

2. (8 – 9a)a = – 40 + (6 – 3a)(6 +3a)

A	B	C	D
– 2	0,5		– 0,5

3. 8m (1 + 2m) – (4m + 3)(4m – 3) = 2m

A	B	C	D
– 1,5		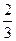1,5	– 15

4. x – 3x (1 – 12x) = 11 – (5 – 6x)(6x + 5)

A	B	C	D
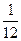
		– 12	– 22

5. (x – 7)² + 3 = (x – 2)(x + 2)

A	B	C	D
– 4	0,25	– 42	4

6. (x+6)² – (x – 5)(x + 5) = 79

A	B	C	D
	1,5		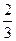– 1,5

V тема. Сумма и разность кубов. Куб суммы и разности двух выражений.

1. а) Найдите значение выражения:

(а + 5)(а² – 5а + 25) – 125 при а = - 3

б) Выполните действия: (а – 2)³

A. a) – 27; б) а³ – 3а²b + 3ab² – b³

B. а) 27; б) а³ + 3а²b – 3ab² – b³

C. а) – 9; б) а³– 8

2. а) Найдите значение выражения:

27 + (с – 3)(с² + 3с + 9) при с = 5

б) Выполните действия: (3 – х)³

A. a) – 125; б) 27 – х³

B. а) 15; б) 27 – 6х² – х³

C. а) 125; б) 27 – 27х + 9х² – х³

3. а) Найдите значение выражения:

(2х – 1)(4х² + 2х + 1) + 4 при х = 4

б) Выполните действия: (2х + у)³

A. a) – 99; б) 8х³ + у³

B. а) 515; б) 8х³ + 12х²у + 6ху² + у³

C. а) 99; б) 2х³ + 3х²у + 3ху² + у³

4. а) Найдите значение выражения:

(х + 4)(х² – 4х + 16) – 63 при х = 0,5

б) Выполните действия: (3а – 2b)³

A. a) 1,125; б) 27а³ – 54а²b + 36ab²- 8b³

B. а) 2,5; б) 27a³ – 8b³

C. а) 0,125; б) 9a³ – 6b³

5. а) Найдите значение выражения:

(5 + x)(25 – 5х + x²) – 125 при х = 0,2

б) Выполните действия: (2a – 1)³

A. a) 0,08; б) 8а³ – 1

B. а) 0,6; б) 2а³ – 12а² + 6а – 1

C. а) 0,008; б) 8а³ – 12а² + 6а – 1

6. а) Найдите значение выражения:

(y – 1)(y² + y + 1) + 5 при y = 0,1

б) Выполните действия: (2b + 1)³

A. a) 4,001; б) 8b³ + 12b² + 6b + 1

B. а) 4,3; б) 8b³ + 6b + 1

C. а) 4,01; б) 8b³ + 1