Применение знаний при решении типовых задач

Применение знаний при решении типовых задач

Задача 1.
В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?
Решение: Событие A-билет выигрышный. Общее число различных исходов есть n=1000
Число исходов, благоприятствующих получению выигрыша, составляет m=200. Согласно формуле P(A)= , получим P(A)= 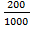= = 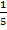0,2

Задача 2.
Из урны, в которой находятся 5 белых и 3 черных шара, вынимают один шар. Найти вероятность того, что шар окажется черным.
Решение: Событие A-появление черного шара. Общее число случаев n=5+3=8
Число случаев m, благоприятствующих появлению события A, равно 3
P(A)= 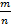= = 0,375

Задача 3.
Из урны, в которой находятся 12 белых и 8 черных шаров, вынимают наудачу два шара. Какова вероятность того, что оба шара окажутся черными?
Решение: Событие A- появление двух черных шаров. Общее число возможных случаев n равно числу сочетаний из 20 элементов (12+8) по 2
n= 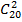= = 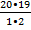190
Число случаев m, благоприятствующих событию A, составляет
n= 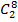= = 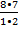28

P(A)= 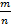= = 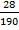= 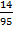0,147

Задача 4.
В одной урне находятся 4 белых и 8 черных шаров, в другой – 3 белых и 9 черных. Из каждой урны вынули по шару. Найти вероятность того, что оба шара окажутся белыми.
Решение:Пусть A - появление белого шара из первой урны, а B – появление белого шара из второй урны. Очевидно, что события A и B независимы. Найдем P(A)=4/12=1/3, P(B)=3/12=1/4, получим
P(AB)=P(A)•P(B)=(1/3)•(1/4)=1/12=0,083

Задача 5.
В ящике находится 12 деталей, из которых 8 стандартных. Рабочий берет наудачу одну за другой две детали. Найти вероятность того, что обе детали окажутся стандартными.
Решение: Введем следующие обозначения: A – первая взятая деталь стандартная; B – вторая взятая деталь стандартная. Вероятность того, что первая деталь стандартная, составляет P(A)=8/12=2/3. Вероятность того, что вторая взятая деталь окажется стандартной при условии, что была стандартной первая деталь, т.е. условная вероятность события B, равна 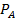(B)=7/11.
Вероятность того, что обе детали окажутся стандартными, находим по теореме умножения вероятностей зависимых событий:
P(AB)=P(A)• 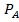(B)=(2/3)•(7/11)=14/33=0,424