Контакты

Случайная статья

Тема: «Применение производных к решению прикладных задач».

Тема: «Применение производных к решению прикладных задач».

Задание 1.

Найти мгновенную скорость точки, движущейся прямолинейно по закону 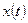в момент времени :

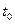1)

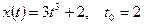
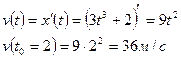
2)

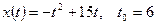
3)

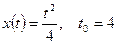
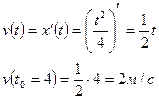
4)

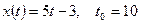
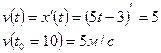
Задание 2.

Составить уравнение касательной и нормали к графику функции 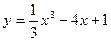в точке .

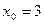Решение.

Запишем уравнение касательной и нормали в общем виде:

- уравнение касательной

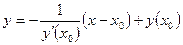- уравнение нормали.

Найдем составляющие данных уравнений.

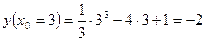
Т.об., уравнение касательной примет вид: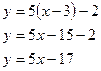

Т.об., уравнение нормали примет вид: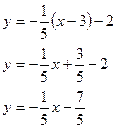

Ответ: 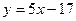- уравнение касательной; 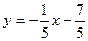- уравнение нормали.

Задание 3

а) Вычислить приближенное значение функции 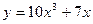в точке .

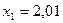Решение.

Для вычисления приближенного значения функции воспользуемся формулой

.

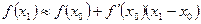В качестве 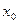возьмем 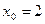. Найдем составляющие данного выражения:

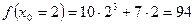
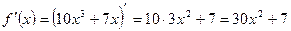
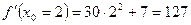
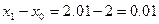
Подставим данные значения формулу и получим:

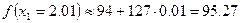
Ответ: приближенное значение функции 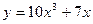в точке 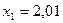, равно примерно 95,27.

б) Найти приближенное значение .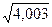

1Решение.

Для вычисления приближенного значения функции воспользуемся формулой

.

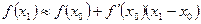Введем обозначения: 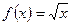, , 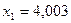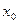– это ближайшее целое значение к 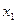, поэтому .

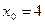Далее вычисляем , , , .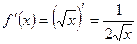

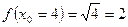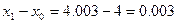Т. об., получаем .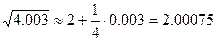

Ответ: приближенное значение 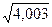равно примерно 2,00075.

Задание 4.

а) Найти интервалы возрастания и убывания функции, точки экстремума .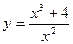

Решение.

1. Найдем область определения функции 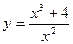. Известно, что дробь определена, если ее знаменатель отличен от нуля. Поэтому получаем,

.

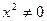
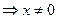Т. об., получаем .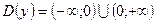

2. Вычисляем производную функции

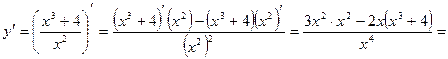
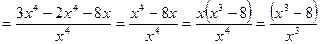
3. Решим уравнение 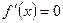. Дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель отличен от нуля. Поэтому получаем систему вида

.

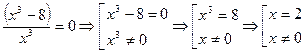
4. Рисуем числовую ось, расставляем числа в порядке возрастания и определяем знаки над промежутками.

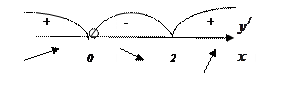
5. Т. об., функция возрастает при 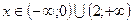и функция убывает при 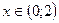. Т. к. в точке 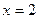происходит смена знаков с «-» на «+», то данная точка является точкой минимума.

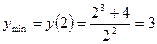.Т.об. 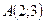- точка локального минимума.

б) Найти наименьшее и наибольшее значение функции 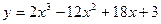на отрезке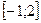

Решение.

1. Найдем производную функции

2. . Решим уравнение .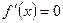

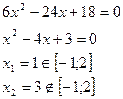
Далее вычисляем значение функции в точке 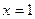и на концах отрезка.

; ;

.

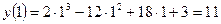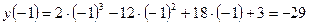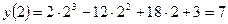Т. об., , .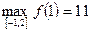

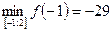© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.