Решение уравнений. Сколько корней будем искать? Что про них можно заранее сказать?. cos0 + isin0), z = r (cosϕ + isinϕ).. z 3= r3 (cos3ϕ + isin3ϕ).. r3 = 1, r – действительное число, значит r = 1;. Сколько корней? В каком поле? Корни р

Решение уравнений

4 Найти в поле С все значении 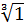(вспомогательное).

В каком виде ответ?

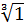= z.

1 = z3.

Сколько корней будем искать? Что про них можно заранее сказать?

Нужно перевести в тригонометрическую форму 1 = r (cosϕ + isinϕ) и перевести в тригонометрическую форму z.

1 = 1 (cos0 + isin0), z = r (cosϕ + isinϕ).

z 3= r3 (cos3ϕ + isin3ϕ).

Имеем: 1 (cos0 + isin0) = r³ (cos3ϕ + isin3ϕ),тогда:

r3 = 1, r – действительное число, значит r = 1;

3ϕ = 0 + 2 k,гдеk –целое число.

Приk₁ = 0: 3ϕ = 0,значит иϕ = 0, то естьz = 1 (cos0 + isin0),

при k₂ = 1: 3ϕ = 2

при k₃ = 2:

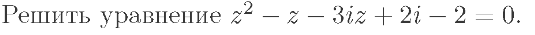
Уравнение квадратное относительно z.

Сколько корней? В каком поле? Корни разные или одинаковые? Могут быть корни сопряженные?

Запишем в явном виде: z²+ (…) z + … = 0

z2 + (-1-3i) z + 2i - 2 = 0 или z2 - (1+3i) z + 2i - 2 = 0

ϕ = = 90⁰

ϕ = - 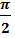= -90⁰

Ответ удовлетворяет предположению?

2. Найти корни многочлена f(x) = 6x³+ 11x²- 3x – 2 = ( х+2) (…), если известно, что один из них равен -2.

Сколько еще корней нужно найти?

Что можно сказать об этих корнях?

Этапы решения

3. Найти корни многочлена f(x) = -x³ - 5x² + 11x - 15, если известно, что один из них равен 1 + 2i.

Сколько еще корней нужно найти?

Что можно сказать об этих корнях?

(1 + 2i) (1 - 2i) = 1+ 4 = 5

(1 + 2i) (1 - 2i)3 = f(x)

Этапы решения

4. Разложить многочлен f(x) = x⁴+ 13x²+ 36 на множители

x⁴+ 13x²+ 36 = (x²+ 4) (x²+ 9)

а) над полем действительных чисел;

б) над полем комплексных чисел: (x - 2 i)(x + 2i)(x – 3i)(x+ 3i).

t² + 13 t + 36 = 0, где t = x²

t₁= -4, t₂= -9.

t² + 13 t + 36 = (t + 4) (t + 9)

Решение уравнений третьей степени

Формулы Д. Кардано.

Решение уравнений четвертой степени.

Формула Феррари.

Ссылка или литература