
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическое занятие №66.. Решение практических задач математической статистики. План проведения. Краткие теоретические сведения. Пример составления закона распределения дискретной случайной величины
Практическое занятие №66.
Решение практических задач математической статистики
Цель занятия:формирование умения решать практические задачи, применяя вероятностные методы
План проведения
1. Запишите тему и цель практического занятия.
2. Изучите теоретические сведения.
3. Ознакомьтесь с образцами выполнения заданий.
4. Выполните практические задания и оформите в соответствии с образцом.
Краткие теоретические сведения
Дискретной случайной величиной называется такая величина, число возможных значений которой либо конечное, либо бесконечное счетное множество, т.е. множество, элементы которого могут быть пронумерованы.
Дискретная случайная величина будет полностью описана с вероятностной точки зрения, если будет указано, какую вероятность имеет каждое из событий, соответствующих значениям случайной величины. Этим устанавливается закон распределения случайной величины.
Способы или формы представления закона распределения случайной величины могут быть различными. Простейшей формой задания закона распределения дискретной случайной величины X является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности.
| X | x1 | x2 | … | xn | … |
| P | p1 | p2 | … | pn | … |
Сумма значений нижней строки данной таблицы должна быть равна единице.
p1+ p2+…+ pn+…=1
Это свойство можно использовать для проверки правильности составления закона распределения.
Пример составления закона распределения дискретной случайной величины

О каждой случайной величине необходимо, прежде всего, знать её среднее значение M(x), около которого группируются возможные значения случайной величины. Эта числовая характеристика случайной величины называется её математическим ожиданием.
Математическое ожидание вычисляется по формуле:
M(x)= x1 p1+ x2 p2+ …+ xn pn.
Ещё одной из самых важных числовых характеристик дискретной случайной величины является дисперсия D(x), характеризующее степень разбросанности значений случайной величины относительно среднего. Дисперсию удобно вычислять по формуле:
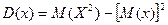
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|