Теоретическая часть

Лабораторно-практическая работа №3

«Исследование основных логических элементов

ИЛИ, И, НЕ, ИЛИ-НЕ, И-НЕ»

Цель работы:

- изучение теоретического материала о работе схем логических элементов ИЛИ, И, НЕ, ИЛИ-НЕ, И-НЕ на дискретных элементах;

- исследование работы логических элементов.

Материальное оснащение:

- персональный компьютер (процессор 386 с ОЗУ не менее 1 Мб);

- монитор с разрешающей способностью не менее 640х480;

- видеокарта, работающая в режиме 640х480 с цветностью не менее 256 цветов;

- операционная система DOS 3.3 и выше;

- манипулятор «мышь»;

- программа анализа электронных схем «Micro-Cap II».

Ход работы.

1. Теоретическая часть

1.1. Общие сведения

Булевы функции двух аргументов ИЛИ (функция логического сложения), И (функция логического умножения), НЕ (функция логического отрицания) составляют полный набор. Другими словами, с помощью этих трех функций можно построить сколь угодно сложную булеву функцию любого числа аргументов.

1.1.1. Логический элемент ИЛИ

Функция ИЛИ - функция логического сложения (дизъюнкция). Она равна единице, если хотя бы один из аргументов равен 1. Для нее можно записать правила сложения: 0+0 = 0; 0+1= 1; 1+0 = 1; 1+1 = 1. Часто вместо этих правил сложения функцию записывают в виде таблицы истинности. Таблица истинности различных состояний для функции ИЛИ приведена в таблице 1. A и B в таблице - это аргументы функции (слагаемые), Y - функция (результат).

Таблица 1

A	B	Y

Если принять 0 как отсутствие напряжения, а 1 как его наличие, то любую булеву функцию можно реализовать в виде электронной схемы, в которой имеются входные клеммы для подачи напряжений, соответствующие аргументам функции (A и B), и выход, напряжение на котором соответствует функции (Y).

В соответствии с рисунком 1 электрическая схема реализует функцию ИЛИ.

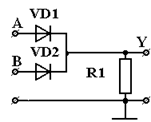
Рисунок 1 - Схема элемента ИЛИ

В этой схеме напряжения (аргументы) подаются на входы A и B по отношению к общему проводу, а выходной сигнал (функция) снимается с выхода Y (также по отношению к общему проводу). Напряжение равное нулю на входе соответствует замыканию этого входа на общий провод. Единственным источником напряжения для этой схемы являются входные сигналы, поэтому для первой строки таблицы истинности при напряжениях на обоих входах равном 0 и на выходе будет нулевое напряжение. Первая строка таблицы истинности выполняется.

Рассмотрим вторую строку таблицы истинности. На входе A напряжение равно 0, значит клемма A закорочена на общий провод. На входе B присутствует напряжение. Диод VD2 пропускает ток, который течет через резистор R и создает на нем падение напряжения. Это напряжение и является выходным, следовательно Y = 1. Диод VD1 находится в закрытом состоянии, так как на его катоде напряжение больше, чем на аноде. Вторая строка таблицы истинности выполняется.

Третья строка аналогична второй, так как входы A и B одинаковы. Для этого случая диод VD1 будет открыт, а диод VD2 закрыт. Реализация 3-й строки также доказана.

В четвертой строке таблицы истинности на оба входа схемы подается напряжение. Открыт один из диодов, на анод которого подается большее напряжение, Y = 1.

Таким образом, доказаны все строчки реализации логической функции ИЛИ .

Для условного обозначения схемы реализации функции ИЛИ используют символ в соответствии с рисунком 2.

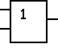
Рисунок 2

1.1.2. Логический элемент И

Функция И - функция логического умножения (конъюнкция). Она равна единице только в том случае, когда оба аргумента равны 1. Таблица истинности различных состояний для функции И приведена в таблице 2.

Таблица 2

A	B	Y

В соответствии с рисунком 3 электрическая схема реализует функцию И.

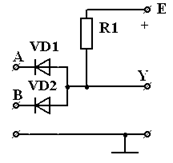
Рисунок 3 - Схема элемента И

Объяснение принципа действия этой схемы так же просто, как и для предыдущей схемы. Если хотя бы на одном из входов напряжение равно 0, то этот вход закорочен на общий провод, соответствующий диод открыт и подсоединен к выходу. Напряжение на открытом диоде близко к нулю, таково же напряжение на выходе Y. Мы сразу доказали три строки таблицы истинности.

Для четвертой строки на оба входа подано напряжение. Если напряжение питания больше входных напряжений, то диоды открыты, и напряжение на выходе равно сумме напряжения на входе и на открытом диоде, т.е. Y = 1. В случае, если напряжение питания меньше входных напряжений, то диоды закрыты, а напряжение на выходе равно напряжение питания. И в этом случае Y = 1.

Для условного обозначения схемы реализации функции И используют символ в соответствии с рисунком 4.

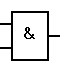
Рисунок 4

1.1.3. Логический элемент НЕ

Функция НЕ - логическое отрицание (инверсия). Функция равна единице при нулевом аргументе и равна нулю при аргументе A равном 1. Таблица истинности различных состояний для функции И приведена в таблице 3.

Таблица 3

A	Y

В соответствии с рисунком 5 электрическая схема реализует функцию НЕ.

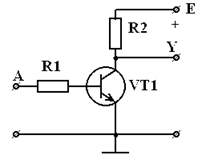
Рисунок 5 - Схема элемента НЕ

При напряжении на входе A равном 0 транзистор VT1 закрыт, напряжение на выходе Y близко к напряжению источника питания. При подаче на вход напряжения, достаточного для отпирания транзистора до насыщения, напряжение на выходе близко к нулю. Таким образом обе строки таблицы истинности выполняются.

Для условного обозначения схемы реализации функции НЕ используют символ в соответствии с рисунком 6.

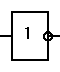
Рисунок 6

1.1.4. Логический элемент ИЛИ-НЕ

Функция ИЛИ-НЕ - функция логического сложения с отрицанием (элемент Пирса). Она равна единице только в том случае, если оба из аргументов равны 0. Таблица истинности различных состояний функции ИЛИ-НЕ приведена в таблице 4.

В соответствии с рисунком 7 электрическая схема реализует функцию ИЛИ-НЕ.

Таблица 4

A	B	Y

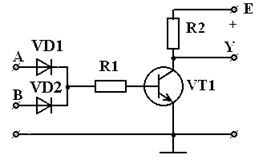
Рисунок 7 - Схема элемента ИЛИ-НЕ

Объяснение принципа действия этой схемы объединяет принципы действия схем ИЛИ и НЕ. Если хотя бы на одном из входов напряжение равно 1, то соответствующий диод открыт и при подаче на вход напряжения, достаточного для отпирания транзистора до насыщения, напряжение на выходе близко к нулю, т.е. Y = 0. Мы сразу доказали три строки таблицы истинности.

Напряжение равное нулю на обоих входах соответствует замыканию этого входа на общий провод. Единственным источником напряжения для открывания транзистора VT1 этой схемы являются входные сигналы, поэтому транзистор закрыт и на выходе Y близко к напряжению источника питания, т.е. Y = 1. Первая строка таблицы истинности выполняется. Таким образом, доказаны все строчки реализации логической функции ИЛИ-НЕ .

Для условного обозначения схемы реализации функции ИЛИ-НЕ используют символ в соответствии с рисунком 8.

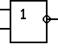
Рисунок 8

1.1.5. Логический элемент И-НЕ

Функция И-НЕ - функция логического умножения с отрицанием (элемент Шеффера). Она равна нулю только в том случае, когда оба аргумента равны 1. Таблица истинности различных состояний функции И-НЕ приведена в таблице 5.

Таблица 5

A	B	Y

В соответствии с рисунком 9 электрическая схема реализует функцию И-НЕ.

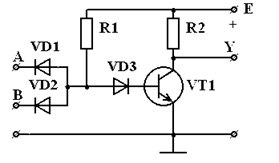
Рисунок 9 - Схема элемента И-НЕ

Объяснение принципа действия этой схемы объединяет принципы действия схем И и НЕ. Если хотя бы на одном из входов напряжение равно 0, то этот вход закорочен на общий провод, соответствующий диод открыт и вход подсоединен к точке соединения резистора R1 с диодом VD3, при этом напряжение в этой точке близко к нулю. В результате диод VD3 закрыт и транзистор VT1 закрыт, напряжение на выходе Y близко к напряжению источника питания, т.е. Y = 1. Мы сразу доказали три строки таблицы истинности. Для четвертой строки на оба входа подано напряжение. В случае, если напряжение питания меньше или равно входных напряжений, то диоды закрыты, а напряжение питания через резистор R1 и открытый диод VD3 подается на вход транзистора VT1 и отпирает его до насыщения, напряжение на выходе равно нулю, т.е. Y = 0.

Таким образом, доказаны все строчки реализации логической функции И-НЕ .

Для условного обозначения схемы реализации функции И-НЕ используют символ в соответствии с рисунком 10.

Рисунок 10

2. Практическая часть

2.1. Изучить теоретическую часть лабораторно-практической работы.

2.2. Запустить на компьютере программу анализа электронных схем.

2.3. Провести исследования процессов в схемах реализующих логические функции.

2.4. Загрузить для исследования файл 4_0, для чего последовательно нажать клавиши “C”, “Y”, “F”, “1”, “4”, “_”, “0”, “Enter”. Последовательное нажатие клавиш “4”, “_”, “0”, - это имя файла.

2.5. Провести анализ схемы, представленной на экране монитора, для чего последовательно нажать клавиши “A”, “1”, “Y”, “Enter”, “Enter”.

2.6. На экране монитора будут графики процессов, происходящих в схеме реализующей логическую функцию, причем на нижнем графике – это входные сигналы (один синего цвета, а второй красного цвета), а на верхнем графике – это выходной сигнал. По оси абсцисс указано время в секундах (S), а по оси ординат - напряжение в вольтах (В). Напряжения для каждого графика указаны справа и слева по оси ординат соответствующими цветами.

2.7. Зарисовать эти графики к себе в тетрадь.

2.8. Измерить на графиках амплитуды входных сигналов U1 и U2 (для синего и красного графика соответственно) и выходного сигнала Uвых в моменты времени: 0,5 с; 1,5 с; 2,5 с; 3,5 с. Записать данные в тетрадь, используя форму таблицы 1.

Таблица 1

Наименование схемы	Время, с	Напряжение, В			Таблица истинности
Наименование схемы	Время, с	U1	U2	Uвых	А	В	Y

2.9. На основании измеренных данных заполнить таблицу истинности для схемы, учитывая, что напряжение от 8 до 10 В – это логическая 1, а напряжение от 0 до 1 В – это логический 0. Для выхода из режима анализа схемы и возврата в режим просмотра схемы необходимо нажать клавишу “3”.

2.10. Загрузить для исследования файл 4_1, для чего последовательно нажать клавиши “C”, “Y”, “F”, “1”, “4”, “_”, “1”, “Enter”.

2.11. Повторить пункты 2.5., 2.6., 2.7, 2.8, 2.9.

2.12. Аналогично схеме из файла 4_1 проведите исследование для схем из файлов 4_2, 4_3 и 4_4. Для схемы 4_2 замеры сделать только в моменты времени 1,5 с и 3,5 с и только напряжений U1, Uвых.

2.13. Выйти из программы, для чего в режиме просмотра схемы необходимо последовательно нажать клавиши “Q”, “Y”.

2.14. На основании анализа каждой заполненной таблицы истинности сделать вывод о реализации схемой логической функции.

3. Контрольные вопросы

3.1. Какое другое название имеет функция логического сложения?

3.1.1. Элемент Пирса.

3.1.2. Инверсия.

3.1.3. Дизъюнкция.

3.1.4. Конъюнкция.

3.1.5. Элемент Шеффера.

3.2. Какое другое название имеет функция логического умножения?

3.2.1. Элемент Пирса.

3.2.2. Инверсия.

3.2.3. Дизъюнкция.

3.2.4. Конъюнкция.

3.2.5. Элемент Шеффера.

3.3. Какое другое название имеет функция логического отрицания?

3.3.1. Элемент Пирса.

3.3.2. Инверсия.

3.3.3. Дизъюнкция.

3.3.4. Конъюнкция.

3.3.5. Элемент Шеффера.

3.4. Какое другое название имеет функция логического сложения с отрицанием?

3.4.1. Элемент Пирса.

3.4.2. Инверсия.

3.4.3. Дизъюнкция.

3.4.4. Конъюнкция.

3.4.5. Элемент Шеффера.

3.5. Какое другое название имеет функция логического умножения с отрицанием?

3.5.1. Элемент Пирса.

3.5.2. Инверсия.

3.5.3. Дизъюнкция.

3.5.4. Конъюнкция.

3.5.5. Элемент Шеффера.

3.6. Какое выражение записано верно для логической схемы И?

3.6.1. F = A*B.

3.6.2. F = A+B.

3.6.3. F = A+B*C.

3.6.4. F=A*B+C.

3.6.5. F=A+B+C.

3.7. Какое выражение записано верно для логической схемы ИЛИ?

3.7.1. F=A+B*C.

3.7.2. F=A+B.

3.7.3. F=A*B+C.

3.7.4. F=A*B.

3.7.5. F=A*B*C.

1.3.8. Какое выражение записано верно для логической схемы И-НЕ?

3.8.1. F=A*B.

_ _

3.8.2. F=A+B.

____

3.8.3. F=A+B.

___

3.8.4. F=AхB.

_ _

3.8.5. F=A*B.

3.9. Какое выражение записано верно для логической схемы ИЛИ-НЕ?

3.9.1. F=A*B.

_ _

3.9.2. F=A+B.

___

3.9.3. F=AхB.

_ _

3.9.4. F=A*B.

____

3.9.5. F=A+B.

3.10. Как называется табличная запись состояний логической схемы И (ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ)?

3.5.1. Таблица размещения.

3.5.2. Функция распределения.

3.5.3. Функция истинности.

3.5.4. Таблица истинности.

3.5.5. Таблица вероятностей.

4. Оформление отчёта

Отчет должен содержать полученные данные в результате выполнения практической части работы и ответы на контрольные вопросы.