
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Филиал Военной академии РВСН им. Петра Великого
Филиал Военной академии РВСН им. Петра Великого
(г. Серпухов Московской области)
Кафедра «Высшей математики»
ЛЕКЦИЯ №13. «Векторные и параметрические функции»
ПО УЧЕБНОЙ ДИСЦИПЛИНЕ: _МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Автор: доцент Борисова В.И.
Рассмотрено и одобрено на заседании кафедры
Протокол № 12 от «25» июня 2013 г.
Серпухов 2013г.
ЛЕКЦИЯ №13.
«Векторные и параметрические функции»
Учебные и воспитательные цели:
1. Дать определение векторных и параметрических функций. сформулировать правила их дифференцирования.
2. Развивать логическое мышление.
3. Формировать навыки ведения конспекта.
Время – 90 мин.
Учебные вопросы и расчет времени:
Вводная часть – 10 мин.
I. Основная часть – 75 мин.
1. Векторные и параметрические функции.
2. Дифференцирование векторных и параметрических функций.
II. Заключительная часть лекции – 5 мин.
литература:
М. Л. Краснов, А. И. Киселев, Г. И. Макаренко, Е. В. Шикин, В. И. Заляпин
Вся высшая математика. Том 1. Учебник. (линейная алгебра и аналитическая геометрия, введение в математический анализ). (рекомендовано Минобразования)задание на самоподготовку
задание на самоподготовку
1. Проработать материалы лекции по конспекту.
Лекция №13.
Векторные и параметрические функции.
Элементы дифференциальной геометрии.
В1. Векторные и параметрические функции, их дифференцирование.
В2. Элементы дифференциальной геометрии.
В1.
1. Векторная функция скалярного аргумента.
 z
z
A(x, y, z)
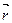
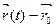
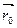
y
х
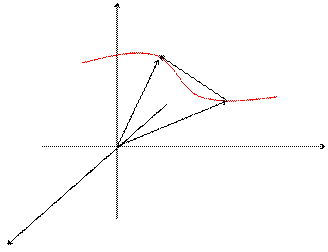
Пусть некоторая кривая в пространстве задана параметрически:
x = j(t); y = y(t); z = f(t);
Радиус- вектор произвольной точки кривой: 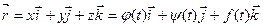 .
.
Таким образом, радиус- вектор точки кривой может рассматриваться как некоторая векторная функция скалярного аргумента t. При изменении параметра t изменяется величина и направление вектора 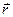 .
.
Запишем соотношения для некоторой точки t0:
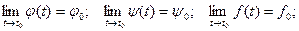
Тогда вектор 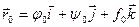 - предел функции
- предел функции 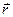 (t).
(t). 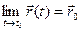 .
.
Очевидно, что
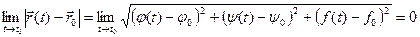 , тогда
, тогда
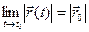 .
.
2. Производная векторной функции скалярного аргумента.
Чтобы найти производную векторной функции скалярного аргумента, рассмотрим приращение радиус- вектора при некотором приращении параметра t.
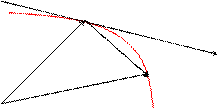 |
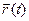
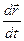
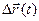
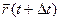
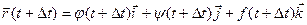 ;
; 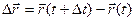 ;
;
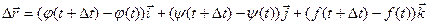
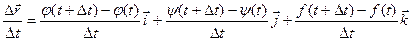
или, если существуют производные j¢(t), y¢(t), f¢(t), то
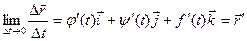
Это выражение – вектор производная вектора 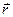 .
.
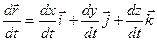
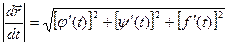
Если имеется уравнение кривой:
x = j(t); y = y(t); z = f(t);
то в произвольной точке кривой А(xА, yА, zА) с радиус- вектором
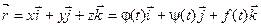
можно провести прямую с уравнением 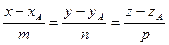
Т.к. производная 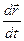 - вектор, направленный по касательной к кривой, то
- вектор, направленный по касательной к кривой, то
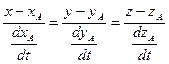 .
.
3. Свойства производной векторной функции скалярного аргумента.
1) 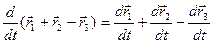
2) 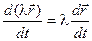 , где l = l(t) – скалярная функция
, где l = l(t) – скалярная функция
3) 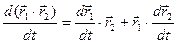
4) 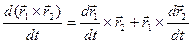
Уравнение нормальной плоскостик кривой будет иметь вид:
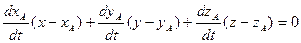
Пример. Составить уравнения касательной и нормальной плоскости к линии, заданной уравнением 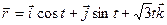 в точке t = p/2.
в точке t = p/2.
Уравнения, описывающие кривую, по осям координат имеют вид:
x(t) = cost; y(t) = sint; z(t) = 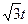 ;
;
Находим значения функций и их производных в заданной точке:
x¢(t) = -sint; y¢(t) = cost; 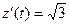
x¢(p/2) = -1; y¢(p/2) = 0; z¢(p/2)= 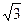
x(p/2) = 0; y(p/2) = 1; z(p/2)= p 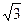 /2
/2
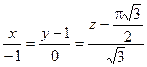
- это уравнение касательной.
Нормальная плоскость имеет уравнение:
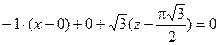
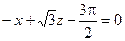
4. Параметрическое задание функции.
Исследование и построение графика кривой, которая задана системой уравнений вида:
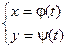 ,
,
производится в общем то аналогично исследованию функции вида y = f(x).
Находим производные:
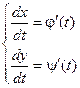
Теперь можно найти производную 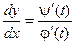 . Далее находятся значения параметра t, при которых хотя бы одна из производных j¢(t) или y¢(t) равна нулю или не существует. Такие значения параметра t называются критическими.
. Далее находятся значения параметра t, при которых хотя бы одна из производных j¢(t) или y¢(t) равна нулю или не существует. Такие значения параметра t называются критическими.
Для каждого интервала (t1, t2), (t2, t3), … , (tk-1, tk) находим соответствующий интервал (x1, x2), (x2, x3), … , (xk-1, xk) и определяем знак производной 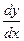 на каждом из полученных интервалов, тем самым определяя промежутки возрастания и убывания функции.
на каждом из полученных интервалов, тем самым определяя промежутки возрастания и убывания функции.
Далее находим вторую производную функции на каждом из интервалов и, определяя ее знак, находим направление выпуклости кривой в каждой точке.
Для нахождения асимптот находим такие значения t, при приближении к которым или х или у стремится к бесконечности, и такие значения t, при приближении к которым и х и у стремится к бесконечности.
В остальном исследование производится аналогичным также, как и исследование функции, заданной непосредственно.
На практике исследование параметрически заданных функций осуществляется, например, при нахождении траектории движущегося объекта, где роль параметра t выполняет время.
Ниже рассмотрим подробнее некоторые широко известные типы параметрически заданных кривых.
5. Уравнения некоторых типов кривых в параметрической
форме.
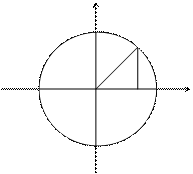 Окружность.
Окружность.
Если центр окружности находится в начале координат, то координаты любой ее
точки могут быть найдены по формулам:
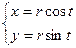 0 £ t £ 3600
0 £ t £ 3600
Если исключить параметр t, то получим каноническое уравнение окружности:
x2 + y2 = r2(cos2t + sin2t) = r2
Эллипс.
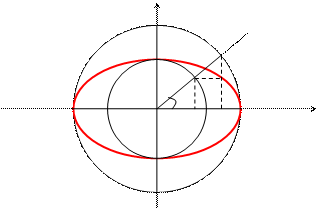 Каноническое уравнение:
Каноническое уравнение: 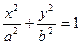 .
.
В
C M(x, y)
t
О N P
Для произвольной точки эллипса М(х, у) из геометрических соображений можно записать: 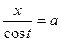 из DОВР и
из DОВР и 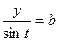 из DOCN, где а- большая полуось эллипса, а b- меньшая полуось эллипса, х и у – координаты точки М.
из DOCN, где а- большая полуось эллипса, а b- меньшая полуось эллипса, х и у – координаты точки М.
Тогда получаем параметрические уравнения эллипса:
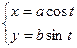
где 0 £ t £ 2p
Угол t называется эксцентрическим углом.
Циклоида.
у
С
М К
О Р В pа 2pа х
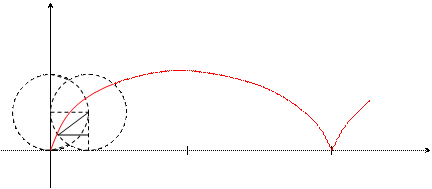
Определение. Циклоидой называется кривая, которую описывает некоторая точка, лежащая на окружности, когда окружность без скольжения катится по прямой.
Пусть окружность радиуса а перемещается без скольжения вдоль оси х. Тогда из геометрических соображений можно записать: OB = 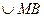 = at; PB = MK = asint;
= at; PB = MK = asint;
ÐMCB = t; Тогда y = MP = KB = CB – CK = a – acost = a(1 – cost).
x = at – asint = a(t – sint).
Итого: 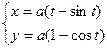 при 0 £ t £ 2p - это параметрическое уравнение циклоиды.
при 0 £ t £ 2p - это параметрическое уравнение циклоиды.
Если исключить параметр, то получаем:
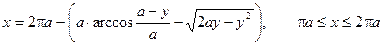
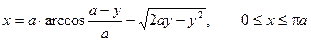
Как видно, параметрическое уравнение циклоиды намного удобнее в использовании, чем уравнение, непосредственно выражающее одну координату через другую.
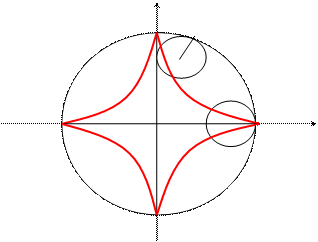
Астроида.
Данная кривая представляет собой траекторию точки окружности радиуса a/4, вращающейся без скольжения по внутренней стороне окружности радиуса a.
 |
a/4
a
Параметрические уравнения, задающие изображенную выше кривую,
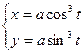 , 0 £ t £ 2p,
, 0 £ t £ 2p,
Преобразуя, получим: x2/3 + y2/3 = a2/3(cos2t + sin2t) = a2/3
6. Производная функции, заданной параметрически.
Пусть 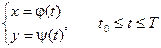
Предположим, что эти функции имеют производные и функция x = j(t) имеет обратную функцию t = Ф(х).
Тогда функция у = y(t) может быть рассмотрена как сложная функция y = y[Ф(х)].
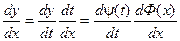
т.к. Ф(х) – обратная функция, то 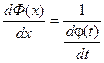
Окончательно получаем: 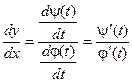
Таким образом, можно находить производную функции, не находя непосредственной зависимости у от х.
Пример. Найти производную функции 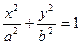
Способ 1: Выразим одну переменную через другую 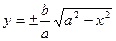 , тогда
, тогда
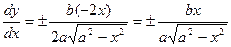
Способ 2: Применим параметрическое задание данной кривой: 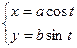 .
.
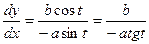
x2 = a2cos2t; 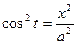
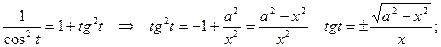
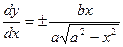
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|