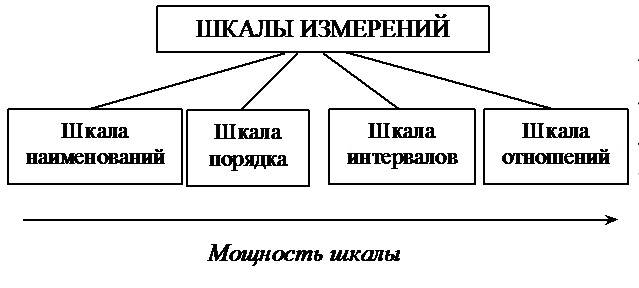
Метрические шкалы

3. Метрические шкалы

Шкала интервалов относится к метрическим шкалам, в которых элементы упорядочены не только по принципу выраженности измеряемого признака, но и на основе ранжирования признаков по размеру, что выражается интервалами между числами, приписываемыми степени выраженности измеряемого признака.

В шкале интервалов нулевая точка отсчета может устанавливаться произвольно, а величины единиц и направление отсчета могут определяться по избираемым константам.

К разряду шкалы интервалов относятся шкалы стандартного IQ-показателя, Т-баллов, процентилей и другие (см. стандартизация, оценки шкальные). Шкалирование в интервальной шкале составляет основу психометрических измерений.

В шкалах отношений (пропорциональных) числовые значения присваиваются объектам таким образом, чтобы между числами и объектами соблюдалась пропорциональность. Начало отсчета в такой шкале фиксировано. Шкала предусматривает операции равенства / неравенства, больше / меньше, равенства интервалов и равенства отношений.

Примером использования такой шкалы в психологических измерениях может служить шкала порогов абсолютной чувствительности анализатора.

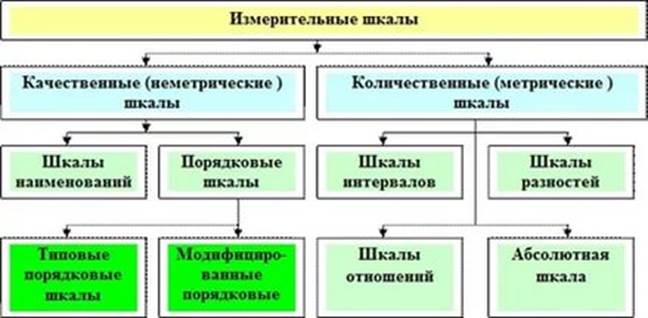
Наряду с делением шкал на метрические и неметрические существует классификация по признаку формы фиксации эмпирических данных, а именно: шкалы вербальные, шкалы числовые и шкалы графические.

В психологической диагностике важным практическим вопросом является оценка надежности, одномерности и обоснованности измерительных шкал. Надежность шкалы определяется на основе анализа устойчивости повторных измерений.

Под валидностью понимается обоснование гипотезы о приспособленности данной шкалы для измерения критериального качества, о полноте его отражения и техническом соответствии самой процедуры шкалирования. Под одномерностью или соразмерностью шкалы понимаются сопоставимость шкалируемых параметров, отсутствие их смещений или пропорциональность между положительными и отрицательными полюсами шкалы, равенство интервалов шкалы или симметричность различных позиций.

⇐ Предыдущая 1 2 34