Как строить эпюру Q по эпюре M

1. Как строить эпюру Q по эпюре M

(или как проверить их соответствие друг другу)

1 правило –определение знака эпюры Q по эпюре М:

Если на эп.М граничная линия эпюры «поворачивается» от «нулевой» линии по часовой стрелке, то Q – положительна; если – против часовой стрелки, то Q – отрицательна. Например:

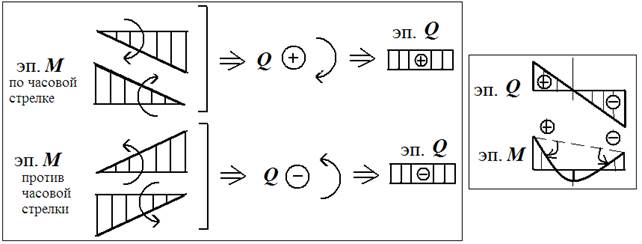
2 правило:определение значений поперечной силы Q по дифференциальной зависимости Q = dM/dx = tg α

а) если эпюра М прямолинейна:

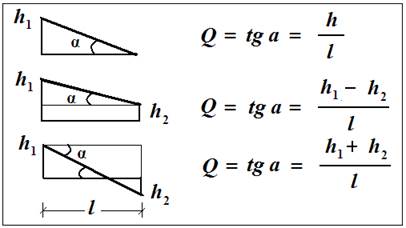
Примеры: Построить эпюру поперечных сил Q.

а) Эпюра моментов М - прямолинейна.

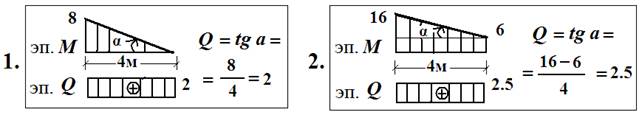
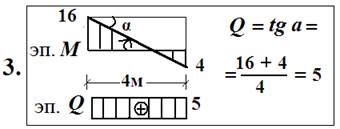
б) Если эпюра моментов – квадратная парабола (на участке – равномерно - распределённая нагрузка). В этом случае пользуются принципом независимости действия сил: сначала определяют поперечную силу от равномерно - распределённой нагрузки - «балочную поперечную силу» Q^б, затемопределяют поперечную силу от изгибающего момента и складывают их.

1-й способ – по формуле: Q = Q^б – М_пр. + М_лев./ l

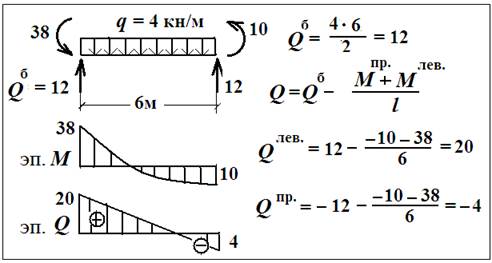
Знаки моментов: плюс + по часовой стрелке, минус - против часовой стрелки.

2-й способ – «визуальный» («по здравому смыслу»):

Сначала определяем реакции от нагрузки: 12, затем – от моментов: 8, затем их складываем: 12+8=20, 12-8=4. Знаки Q определяем, как обычно.

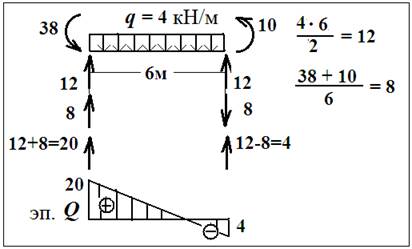
2. Как найти экстремальный момент?

Его надо искать в том сечении, где Q = 0 (меняет знак).

(Q = dM/dx ; из математики: в экстремальных значениях функции первая производная равна нулю).

Объяснение на примере:

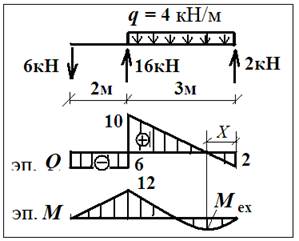
1-й способ(для студентов):

1) отмечаем Х;

2) выражаем Q_x через Х, приравнивая её к нулю. Находим Х:

Q_x= ‒ 2 + 4·Х = 0; Х = 0.5м;

3) определяем М_ех по правилу: М_ех = 2·Х ‒ 4·Х· Х/2 = 2·0.5 – 4·0.5·0.25 = 0.5.

2-й способ – по дифференциальным зависимостям:q = 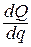= tgα;

Рассматриваем треугольник на эпюре Q: Х=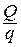

(более простой, особенно в примерах с большим количеством участков).

1) отмечаем Х;

2) Находим Х = Q/q = 2/4 = 0.5.

3) определяем М_ех по правилу: М_ех = 2·Х ‒ 4·Х· Х/2 = 2·0.5 – 4·0.5·0.25 = 0.5.