
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
ДОМАШНЕЕ ЗАДАНИЕ № 1
ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
1. ABCDEF – правильный шестиугольник. Выразить векторы 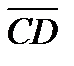 и
и 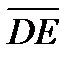 через векторы
через векторы 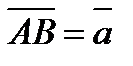 и
и 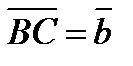 .
.
2. Разложить вектор 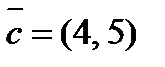 по векторам
по векторам 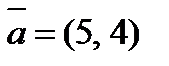 и
и 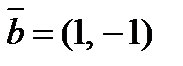 .
.
3. Вычислить 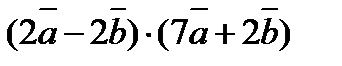 , если
, если 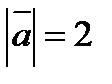 ,
, 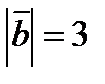 ,
, 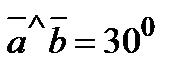 .
.
4. Вычислить проекцию вектора 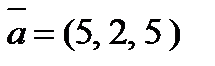 на ось вектора
на ось вектора 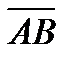 , если A(-1, 1, 0) и B(1, 0, 2).
, если A(-1, 1, 0) и B(1, 0, 2).
5. При каком значении a векторы 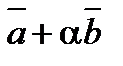 и
и 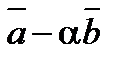 будут ортогональны, если
будут ортогональны, если 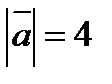 и
и 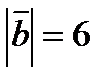 ?
?
6. Найти 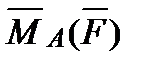 – момент силы
– момент силы 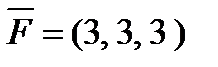 , приложенной в точке B(3, -1, 5), относительно точки A(4, -2, 3).
, приложенной в точке B(3, -1, 5), относительно точки A(4, -2, 3).
7. Вычислить 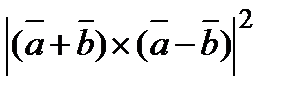 , если
, если 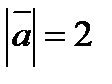 ,
, 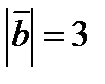 и
и 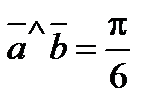
8. При каком значении l векторы  ,
, 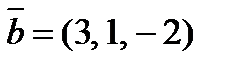 и
и 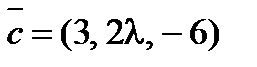 будут компланарны?
будут компланарны?
9. Составить уравнение прямой, проходящей через точку A(2, -3) параллельно прямой, соединяющей точки B (1, 2 ) и С (-1, -5 ).
10. Составить уравнения сторон квадрата, если известны координаты вершины A(-1, 8) и уравнения диагоналей AC: 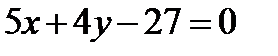 , BD:
, BD: 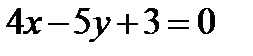 .
.
11. Составить уравнение плоскости, которая проходит через точку A(2, 1, -1) параллельно плоскости 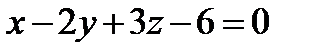 .
.
12. Составить канонические уравнения прямой, проходящей через две заданные точки: а) A( 1, -2, 1) и B( 3, 1, -1); б) A(3, 0, -1) и B(-1, -1, 1).
13. Составить уравнение плоскости, проходящей через прямую 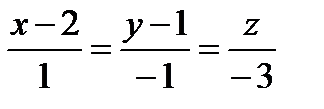 и точку A(2, 3, 0).
и точку A(2, 3, 0).
14. Вычислить определитель третьего порядка по правилу треугольников, разложив по первой строке:
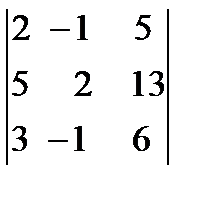 .
.
15. Решить систему уравнений тремя способами: а) методом Гаусса; б) по формулам Крамера; в) записать систему в матричной форме и решить ее с помощью обратной матрицы.
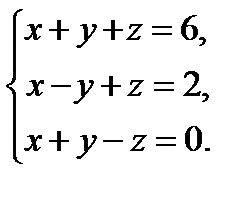
16. Исследовать систему уравнений на совместность и в случае совместности найти ее решение.
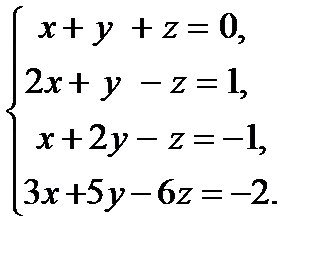 .
.
ВАРИАНТ 2
1. В параллелограмме ABCD 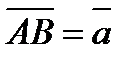 ,
, 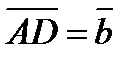 . Выразить через
. Выразить через 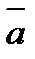 и
и 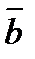 векторы
векторы 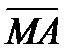 и
и 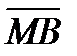 , если М точка пересечения диагоналей параллелограмма.
, если М точка пересечения диагоналей параллелограмма.
2. Разложить вектор 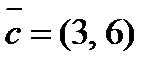 по векторам
по векторам 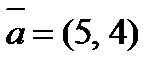 и
и  .
.
3. Вычислить 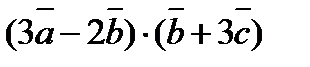 , если
, если 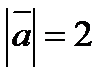 ,
, 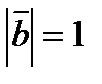 ,
, 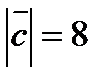 ,
, 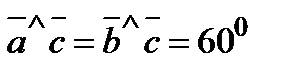 ,
, 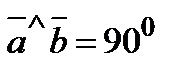 .
.
4. Вычислить проекцию вектора 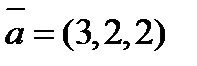 на ось вектора
на ось вектора 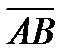 , если A(1, -2, 7) и B(4, 2, 7).
, если A(1, -2, 7) и B(4, 2, 7).
5. При каком значении a векторы 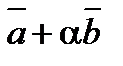 и
и 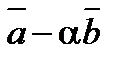 будут ортогональны, если
будут ортогональны, если 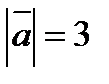 и
и 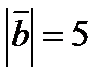 ?
?
6. Найти 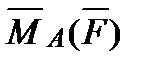 – момент силы
– момент силы 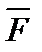 = (4, 4, 4), приложенной в точке B(4, -2, 5), относительно точки A(5, -3, 3).
= (4, 4, 4), приложенной в точке B(4, -2, 5), относительно точки A(5, -3, 3).
7. Найти площадь параллелограмма, построенного на векторах 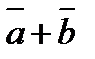 и
и 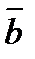 как на сторонах, если
как на сторонах, если 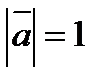 ,
, 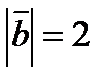 и
и 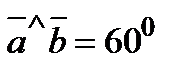 .
.
8. При каком значении l векторы 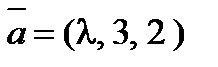 ,
, 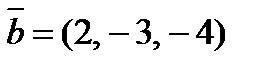 и
и 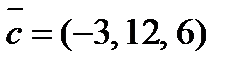 будут компланарны?
будут компланарны?
9. Составить уравнение прямой, проходящей через точку A(1, 2) параллельно прямой, соединяющей точки B(-1, 0) и С(2, 3).
10. Составить уравнения сторон квадрата, если известны координаты вершины A(0, 6) и уравнения диагоналей AC: 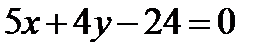 , BD:
, BD: 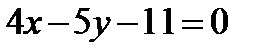 .
.
11. Составить уравнение плоскости, которая проходит через точку A(1, -1, 0) параллельно плоскости 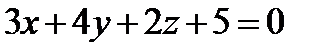 .
.
12. Составить канонические уравнения прямой, проходящей через две заданные точки: а) A(0, -2, 3) и B (3, -2, 1); б) A (1, 2, -4) и B(0, 1, -1).
13. Составить уравнение плоскости, проходящей через прямую 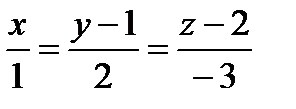 и точку A(1, 2, 3).
и точку A(1, 2, 3).
14. Вычислить определитель третьего порядка по правилу треугольников, разложив по второй строке:
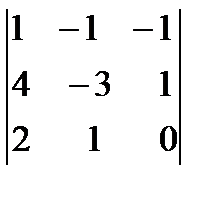 .
.
15. Решить систему уравнений тремя способами: а) методом Гаусса; б) по формулам Крамера; в) записать систему в ма-тричной форме и решить ее с помощью обратной матрицы.
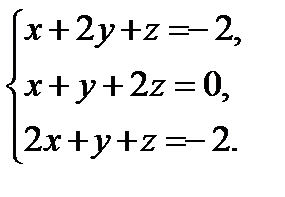
16. Исследовать систему уравнений на совместность и в случае совместности найти ее решение .
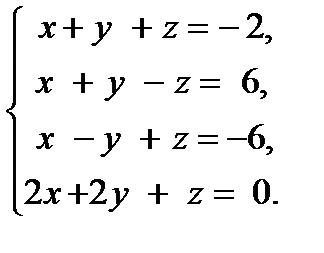
ВАРИАНТ 3
1. В треугольнике ABC медианы 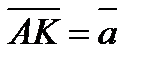 и
и 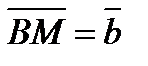 . Выразить через
. Выразить через 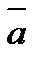 и
и 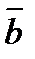 вектор
вектор 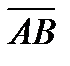 .
.
2. Разложить вектор 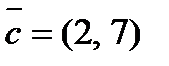 по векторам
по векторам 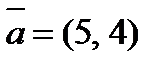 и
и 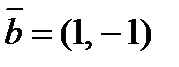 .
.
3. Вычислить 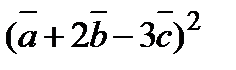 , если
, если 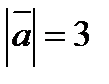 ,
, 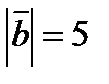 ,
, 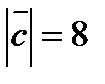 ,
, 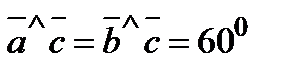 и
и 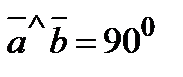 .
.
4. Вычислить проекцию вектора 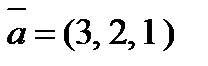 на ось вектора
на ось вектора 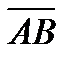 , если A(2, -2, 0) и B(-2, 2, 2).
, если A(2, -2, 0) и B(-2, 2, 2).
5. При каком значении a векторы 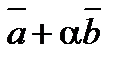 и
и 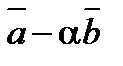 будут ортогональны, если
будут ортогональны, если 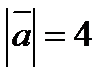 и
и 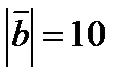 ?
?
6. Найти 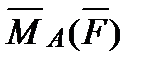 – момент силы
– момент силы 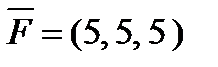 , приложенной в точке B(5, -3, 5), относительно точки A (6, -4, 3).
, приложенной в точке B(5, -3, 5), относительно точки A (6, -4, 3).
7. При каком значении a векторы 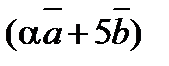 и
и 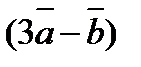 будут коллинеарны, если
будут коллинеарны, если 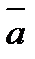 и
и 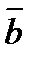 не коллинеарны.
не коллинеарны.
8. При каком значении l векторы 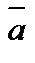 = (1, 3, λ),
= (1, 3, λ), 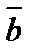 = (4, 5, –1) и
= (4, 5, –1) и 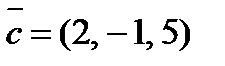 будут компланарны?
будут компланарны?
9. Составить уравнение прямой, проходящей через точку A(2, -2) параллельно прямой, соединяющей точки B(-5, 4) и C(0, 2).
10. Составить уравнения сторон квадрата, если известны координаты вершины A(-2, 10) и уравнения диагоналей AC: 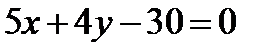 , BD:
, BD: 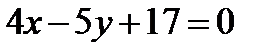 .
.
11. Составить уравнение плоскости, которая проходит через точку A(0, -1, -2) параллельно плоскости  .
.
12. Составить канонические уравнения прямой, проходящей через две заданные точки: а) A(4, 5, 13) и B(-6, 0, 1); б) A(-11, 0, 10) и B( 1, 2, 3).
13. Составить уравнение плоскости, проходящей через прямую 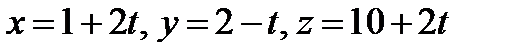 и точку A( 7, 5, 3).
и точку A( 7, 5, 3).
14. Вычислить определитель третьего порядка по правилу треугольников, разложив по третьей строке:
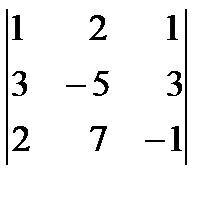 .
.
15. Решить систему уравнений тремя способами: а) методом Гаусса; б) по формулам Крамера; в) записать систему в ма-тричной форме и решить ее с помощью обратной матрицы.
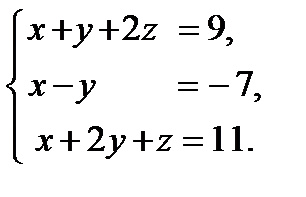
16. Исследовать систему уравнений на совместность и в случае совместности найти ее решение .
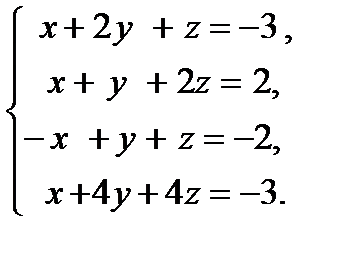
ВАРИАНТ 4
1. В трапеции ABCD отношение длины основания AD к длине основания BC равно 2. Выразить вектор 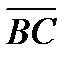 через
через 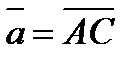 и
и 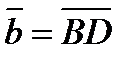 .
.
2. Разложить вектор 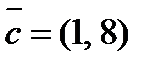 по векторам
по векторам 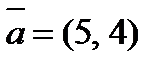 и
и 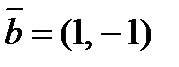 .
.
3. Вычислить 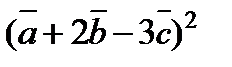 , если
, если 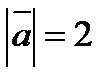 ,
, 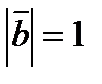 ,
, 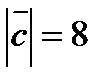 ,
, 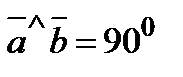 и
и  .
.
4. Вычислить проекцию вектора 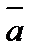 = (1, 2, 3) на ось вектора
= (1, 2, 3) на ось вектора 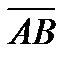 , если A (-3, 1, 4) и B(3, 3, 1).
, если A (-3, 1, 4) и B(3, 3, 1).
5. При каком значении a векторы 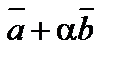 и
и 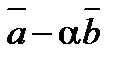 будут ортогональны, если
будут ортогональны, если 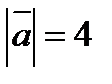 и
и 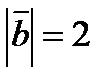 ?
?
6. Найти 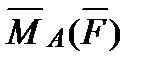 – момент силы
– момент силы 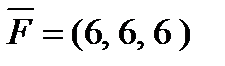 , приложенной в точке B(6, -4, 5), относительно точки A (7, -5, 3).
, приложенной в точке B(6, -4, 5), относительно точки A (7, -5, 3).
7. Найти площадь треугольника с вершинами A(-1, 2, 3), B(5, 1, 4) и C(3, 2, 2).
8. При каком значении l векторы 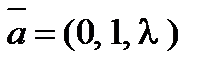 ,
, 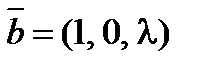 и
и 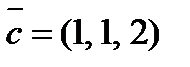 будут компланарны?
будут компланарны?
9. Составить уравнение прямой, проходящей через точку A(-3, 2) параллельно прямой, соединяющей точки B( 2, 1) и C(-5, -1).
10. В квадрате ABCD задана вершина A(-1, -1) и точка пересечения диагоналей K(1,5; 2,5). Составить уравнения сторон и найти координаты остальных вершин.
11. Составить уравнение плоскости, которая проходит через начало координат параллельно плоскости 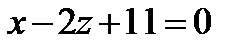 .
.
12. Составить параметрические уравнения прямой, проходя-щей через точку A(7, 3,-2) параллельно вектору 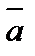 =(1, 2,–1).
=(1, 2,–1).
13. Составить уравнение плоскости, проходящей через прямую 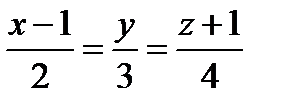 и точку A(-3, -5, 1).
и точку A(-3, -5, 1).
14. Вычислить определитель третьего порядка по правилу треугольников, разложив по первому столбцу:
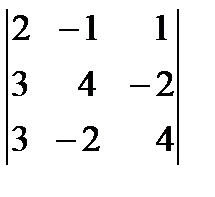 .
.
15. Решить систему уравнений тремя способами: а) методом Гаусса; б) по формулам Крамера; в) записать систему в ма-тричной форме и решить ее с помощью обратной матрицы.
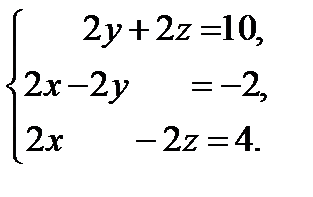
16. Исследовать систему уравнений на совместность и в случае совместности найти ее решение.
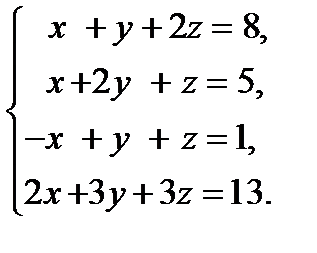
ВАРИАНТ 5
1. В треугольнике ABC точка М делит сторону AC на отрезки AM = 2 и MC = 3, а точка N делит сторону BC на отрезки BN = 3 и NC = 2. Выразить вектор 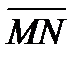 через векторы
через векторы 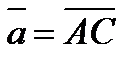 и
и 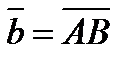 .
.
2. Разложить вектор 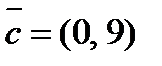 по векторам
по векторам 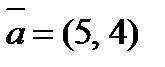 и
и 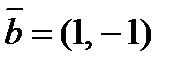 .
.
3. Вычислить 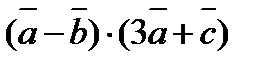 , если
, если 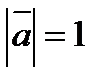 ,
, 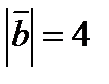 ,
, 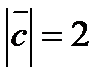 ,
, 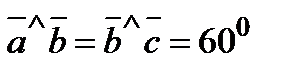 и
и 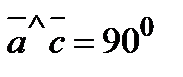 .
.
4. Вычислить проекцию вектора 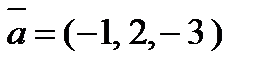 на ось вектора
на ось вектора 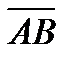 , если A(5, -5, 5) и B(5, 3, 1).
, если A(5, -5, 5) и B(5, 3, 1).
5. При каком значении a векторы 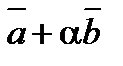 и
и 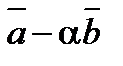 будут ортогональны, если
будут ортогональны, если 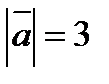 и
и 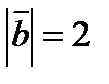 ?
?
6. Найти  – момент силы
– момент силы 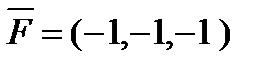 , приложенной в точке B(8, -6, -5), относительно точки A(9, -7, 3).
, приложенной в точке B(8, -6, -5), относительно точки A(9, -7, 3).
7. Найти площадь параллелограмма, построенного на векторах 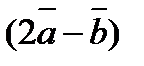 и
и 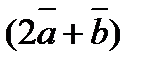 как на сторонах, если
как на сторонах, если 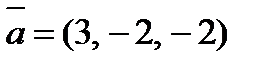 ,
, 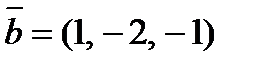 .
.
8. При каком значении l векторы 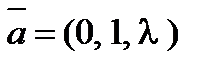 ,
, 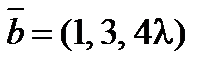 и
и 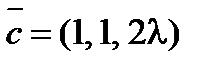 будут компланарны?
будут компланарны?
9. Составить уравнение прямой, проходящей через точку A(-2, -2) параллельно прямой, соединяющей точки B(0, 7) и С(7, 0).
10. В квадрате ABCD задана вершина A(1, 1) и точка пересечения диагоналей K(2,5; 3,5). Составить уравнения сторон и найти координаты остальных вершин.
11. Составить уравнение плоскости, которая проходит через начало координат параллельно плоскости 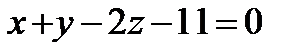 .
.
12. Составить канонические и параметрические уравнения прямой, проходящей через точку A(2, 0, 2) параллельно прямой: 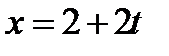 ,
, 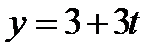 ,
,  .
.
13. Составить уравнение плоскости, проходящей через прямую 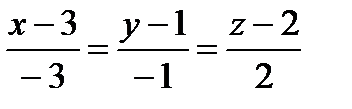 и точку A(-1, -1, 0).
и точку A(-1, -1, 0).
14. Вычислить определитель третьего порядка по правилу треугольников, разложив по второму столбцу:
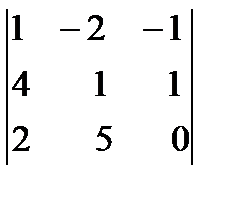 .
.
15. Решить систему уравнений тремя способами: а) методом Гаусса; б) по формулам Крамера; в) записать систему в ма-тричной форме и решить ее с помощью обратной матрицы.
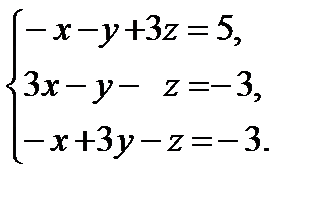
16. Исследовать систему уравнений на совместность и в случае совместности найти ее решение .
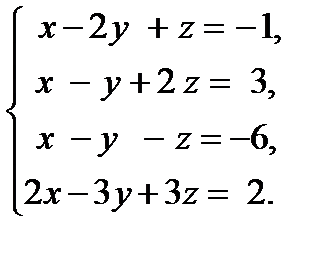
ВАРИАНТ 6
1. В треугольнике ABC точка М делит сторону AC на отрезки AM = 1 и MC = 3, а точка N делит сторону AB на отрезки AN = 3 и NB = 2. Выразить вектор 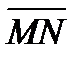 через векторы
через векторы 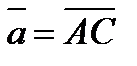 и
и 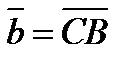 .
.
2. Разложить вектор 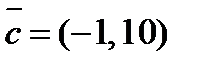 по векторам
по векторам 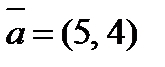 и
и 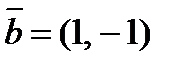 .
.
3. Вычислить 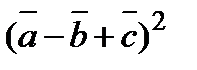 , если
, если 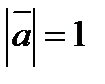 ,
, 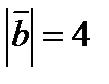 ,
, 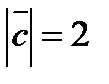 ,
, 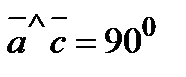 и
и 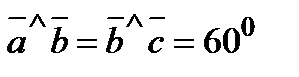 .
.
4. Вычислить проекцию вектора 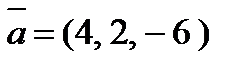 на ось вектора
на ось вектора 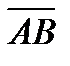 , если A(2, -2, 1) и B(3, -1, 0).
, если A(2, -2, 1) и B(3, -1, 0).
5. Определить косинус угла между векторами 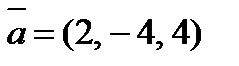 и
и 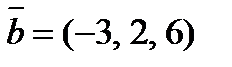 .
.
6. Найти 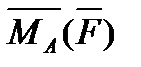 – момент силы
– момент силы 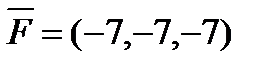 , приложенной в точке B(5, -6, 2), относительно точки A(9, 3, 1).
, приложенной в точке B(5, -6, 2), относительно точки A(9, 3, 1).
7. Найти площадь треугольника с вершинами A(2, 3, 4), B(1, 0, 6) и C(4, 5, -2).
8. При каком значении l векторы 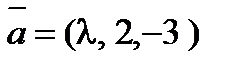 ,
, 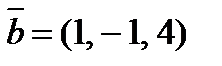 и
и 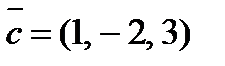 будут компланарны?
будут компланарны?
9. Составить уравнение прямой, проходящей через точку A(1, 6) перпендикулярно к прямой, соединяющей точки B(-1, 4) и С(-2, 3).
10. В квадрате ABCD задана вершина A(2, 2) и точка пересечения диагоналей K(3,5; 4,5). Составить уравнения сторон и найти координаты остальных вершин .
11. Точка P(0, -1, -2) служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составить уравнение этой плоскости.
12. Составить параметрические уравнения прямой, проходя-щей через две заданные точки: а) A(3, -1, 2) и B(2, 1, 1); б) A(1, 1, -2) и B(3, -1, 0).
13. Составить уравнение плоскости, проходящей через прямую 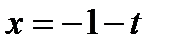 ,
, 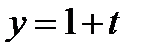 ,
, 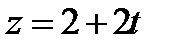 и точку A(2, 1, -3).
и точку A(2, 1, -3).
14. Вычислить определитель третьего порядка по правилу треугольников, разложив по третьему столбцу:
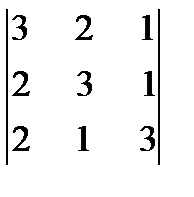 .
.
15. Решить систему уравнений тремя способами: а) методом Гаусса; б) по формулам Крамера; в) записать систему в ма-тричной форме и решить ее с помощью обратной матрицы.
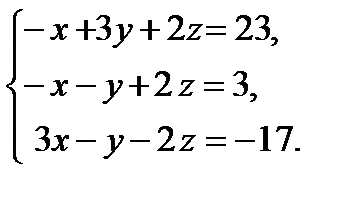
16. Исследовать систему уравнений на совместность и в случае совместности найти ее решение.
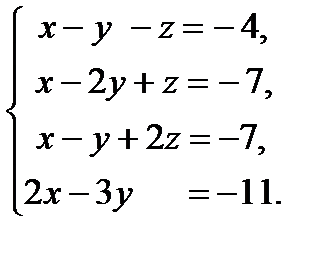
ВАРИАНТ 7
1. В треугольнике ABC точка М делит сторону AB на отрезки AM = 1 и MB = 3, а точка N делит сторону BC на отрезки BN = 2 и NC = 3. Выразить вектор 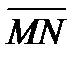 через векторы
через векторы 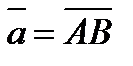 и
и 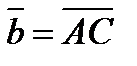 .
.
2. Разложить вектор 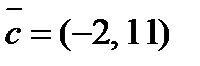 по векторам
по векторам 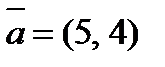 и
и 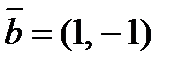 .
.
3. Вычислить 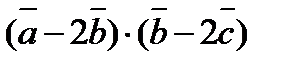 , если
, если 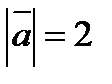 ,
, 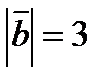 ,
, 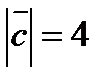 ,
, 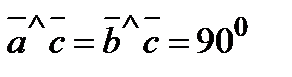 и
и 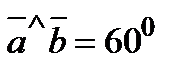 .
.
4. Вычислить проекцию вектора 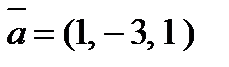 на ось вектора
на ось вектора 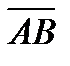 , если A(-5, 7, -6) и B(7, -9, 9).
, если A(-5, 7, -6) и B(7, -9, 9).
5. Вектор 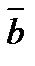 коллинеарен вектору
коллинеарен вектору 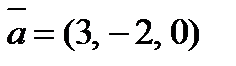 . Найти
. Найти 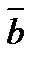 , если
, если 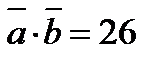 .
.
6. Найти 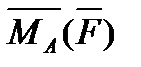 – момент силы
– момент силы 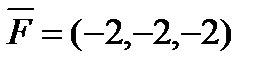 , приложенной в точке B(9, -7, 5), относительно точки A(10, -8, 3).
, приложенной в точке B(9, -7, 5), относительно точки A(10, -8, 3).
7. Найти площадь параллелограмма, построенного на векторах 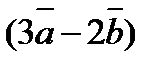 и
и 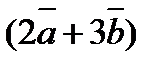 как на сторонах, если
как на сторонах, если 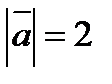 ,
, 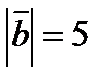 и
и 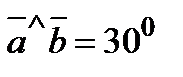 .
.
8. Лежат ли точки A(1, 2, -1), B(0, 1, 5), C(-1, 2, 1) и D(2, 1, 3) в одной плоскости?
9. Составить уравнение прямой, проходящей через точку A(1, 3) перпендикулярно к прямой, соединяющей точки B(2, -1) и С(-8, 2).
10. Известна точка пересечения диагоналей квадрата K(1,5; 3,5) и уравнение одной из его сторон 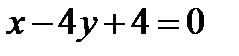 . Найти координаты вершин квадрата и составить уравнения его диагоналей.
. Найти координаты вершин квадрата и составить уравнения его диагоналей.
11. Точка P(-2, 1, -2) служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составить уравнение этой плоскости.
12. Через точки A(12, -6, 1) и B(-6, 6, -5) проведена прямая. Определить точки пересечения этой прямой с координат-ными плоскостями.
13. Найти основание перпендикуляра, опущенного из точки A(3, 0, 4) на плоскость p: 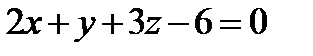 .
.
14. Вычислить определитель третьего порядка по правилу треугольников, разложив по первой строке:
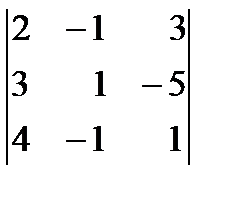 .
.
15. Решить систему уравнений тремя способами: а) методом Гаусса; б) по формулам Крамера; в) записать систему в ма-тричной форме и решить ее с помощью обратной матрицы.
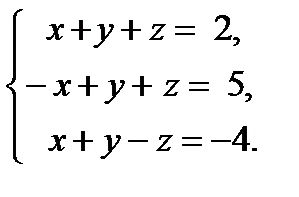
16. Исследовать систему уравнений на совместность и в случае совместности найти ее решение .
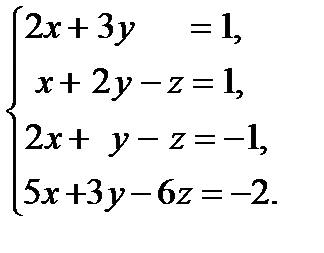
ВАРИАНТ 8
1. В ромбе ABCD точка М делит сторону BC на отрезки BM = 2 и MC = 3, а точка N делит сторону AD на отрезки AN = 4 и ND = 1. Выразить вектор 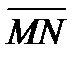 через векторы
через векторы 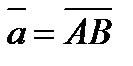 и
и 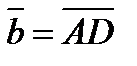 .
.
2. Разложить вектор 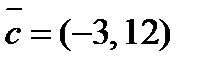 по векторам
по векторам 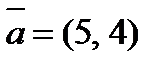 и
и 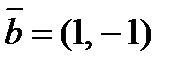 .
.
3. Вычислить 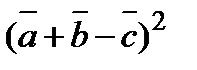 , если
, если 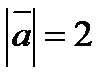 ,
, 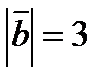 ,
, 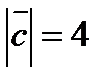 ,
, 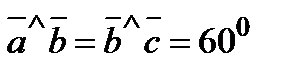 и
и 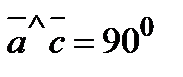 .
.
4. Вычислить проекцию вектора 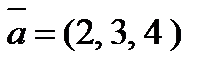 на ось вектора
на ось вектора 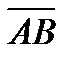 , если A (1, 1, 1) и B(3, 3, 2).
, если A (1, 1, 1) и B(3, 3, 2).
5. Определить косинус угла между векторами 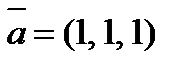 и
и  .
.
6. Найти 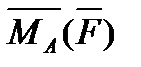 – момент силы
– момент силы 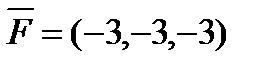 , приложенной в точке B(10, -8, 5), относительно точки A(11, -9, 3).
, приложенной в точке B(10, -8, 5), относительно точки A(11, -9, 3).
7. Найти площадь треугольника, построенного на векторах 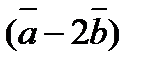 и
и 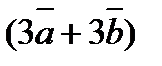 как на сторонах, если
как на сторонах, если 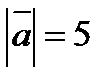 ,
, 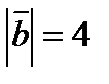 и
и 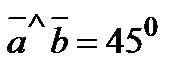 .
.
8. Лежат ли точки A(2,-1,-1), B(5, 5, 4), C(3, 2, -1) и D(4, 1, 3) в одной плоскости?
9. Составить уравнение прямой, проходящей через точку A(-7, 1) и перпендикулярной к прямой, соединяющей точки B(0, -2) и С(7, 1).
10. Известна точка пересечения диагоналей квадрата K(2,5; 2,5) и уравнение одной из его сторон 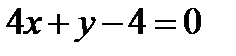 . Найти координаты вершин квадрата и составить уравнения его диагоналей.
. Найти координаты вершин квадрата и составить уравнения его диагоналей.
11. Составить уравнение плоскости, проходящей через точку C(3, 13, 7) перпендикулярно вектору 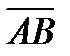 , если A(-1, 0, 2) и B(2, 0, -1).
, если A(-1, 0, 2) и B(2, 0, -1).
12. Составить параметрические уравнения прямой, проходя-щей через две заданные точки: а) A(2, 3, -1) и B(-1, 2, 3); б) A(0, 1, 2) и B(2, 0, 1).
13. Найти основание перпендикуляра, опущенного из точки A(1, 1, 3) на плоскость p: 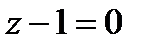 .
.
14. Вычислить определитель третьего порядка по правилу треугольников, разложив по второй строке:
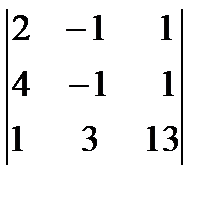 .
.
15. Решить систему уравнений тремя способами: а) методом Гаусса; б) по формулам Крамера; в) записать систему в ма-тричной форме и решить ее с помощью обратной матрицы.
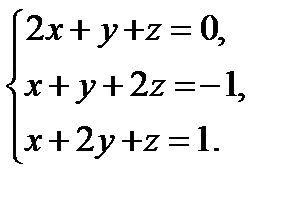
16. Исследовать систему уравнений на совместность и в случае совместности найти ее решение .
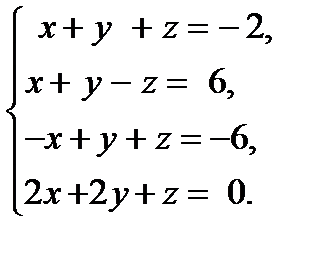
ВАРИАНТ 9
1. В треугольнике ABC AK и BM – медианы. Выразить вектор 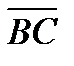 через векторы
через векторы 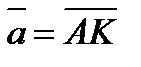 и
и 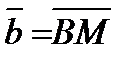 .
.
2. Разложить вектор 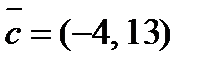 по векторам
по векторам 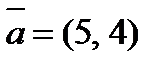 и
и 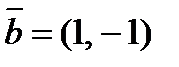 .
.
3. Вычислить 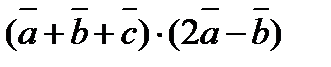 , если
, если 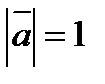 ,
, 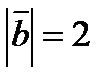 ,
, 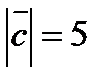 ,
, 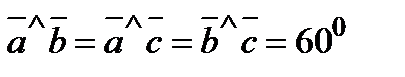 .
.
4. Вычислить проекцию вектора 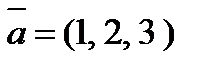 на ось вектора
на ось вектора 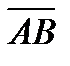 , если A(0, 0, 0) и B(4, 4, 2).
, если A(0, 0, 0) и B(4, 4, 2).
5. Определить косинус внутреннего угла при вершине A треугольника АВС, если A(1, 2, 1), B(3, -1, 1), C(0, 2, -1).
6. Найти 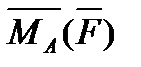 – момент силы
– момент силы 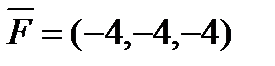 , приложенной в точке B(11, -9, 5), относительно точки A(12, -10, 3).
, приложенной в точке B(11, -9, 5), относительно точки A(12, -10, 3).
7. Найти a и β, при которых вектор 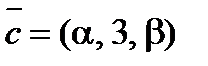 коллинеарен вектору
коллинеарен вектору 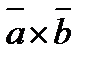 , если
, если 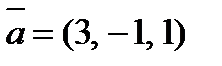 ,
, 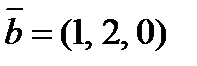 .
.
8. Лежат ли точки A(0, 1, -2), B(-2, 4, 1), C(5, 3, 7) и D(4, 0, 3) в одной плоскости?
9. Найти точку A, симметричную точке B(-2, 1) относительно прямой 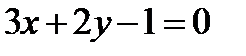 .
.
10. Известна точка пересечения диагоналей квадрата K(1,5; 2,5) и уравнение одной из его сторон 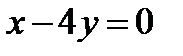 . Найти координаты вершин квадрата и составить уравнения его диагоналей.
. Найти координаты вершин квадрата и составить уравнения его диагоналей.
11. Составить уравнение плоскости, проходящей через точку A перпендикулярно вектору 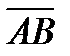 , если A(-1, 2,-3) и B(0, -1, 1)
, если A(-1, 2,-3) и B(0, -1, 1)
12. Через точки A(0, -1, -2) и B(2, 1, 0) проведена прямая. Определить точки пересечения этой прямой с координат-ными плоскостями.
13. Найти основание перпендикуляра, опущенного из точки A(-3, 2, 2) на плоскость p: 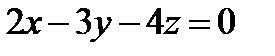 .
.
14. Вычислить определитель третьего порядка по правилу треугольников, разложив по третьей строке:
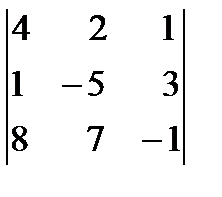 .
.
15. Решить систему уравнений тремя способами: а) методом Гаусса; б) по формулам Крамера; в) записать систему в ма-тричной форме и решить ее с помощью обратной матрицы.
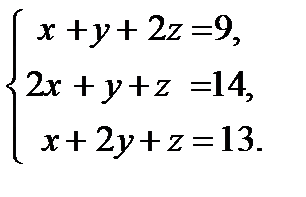
16. Исследовать систему уравнений на совместность и в случае совместности найти ее решение.
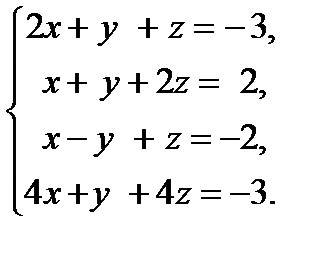
ВАРИАНТ 10
1. В параллелограмме ABCD выразить векторы 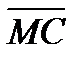 и
и 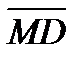 через векторы
через векторы 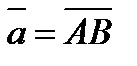 и
и 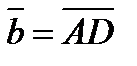 , если М – точка пересече-ния диагоналей параллелограмма.
, если М – точка пересече-ния диагоналей параллелограмма.
2. Разложить вектор 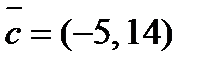 по векторам
по векторам 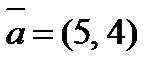 и
и 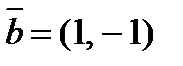 .
.
3. Вычислить 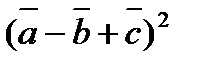 , если
, если 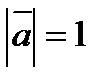 ,
, 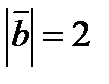 ,
, 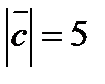 ,
, 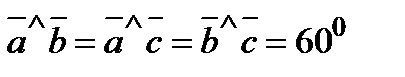 .
.
4. Вычислить проекцию вектора 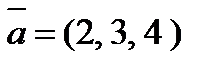 на ось вектора
на ось вектора 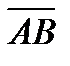 , если A(1, 1, 1) и B(3, 5, 5).
, если A(1, 1, 1) и B(3, 5, 5).
5. Определить косинус угла между векторами 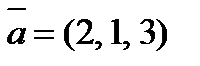 и
и 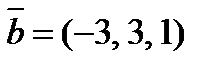 .
.
6. Найти  – момент силы
– момент силы 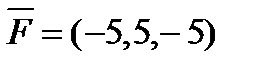 , приложенной в точке B(12, -10, 5), относительно точки A(13, -11, 3).
, приложенной в точке B(12, -10, 5), относительно точки A(13, -11, 3).
7. Найти координаты вектора 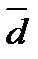 , коллинеарного вектору
, коллинеарного вектору 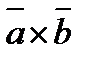 , если
, если 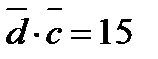 ,
, 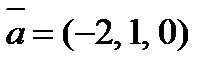 ,
, 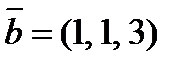 и
и 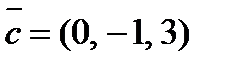 .
.
8. Лежат ли точки A(- 1, -1, -1), B(1, -2, -2), C(0, -2, -1) и D(2, -3, -2) в одной плоскости?
9. Найти точку A, симметричную точке B(1, 2) относительно прямой 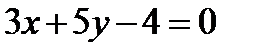 .
.
10. Известна точка пересечения диагоналей квадрата K(2,5; 4,5) и уравнение одной из его сторон 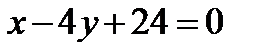 . Найти координаты вершин квадрата и составить уравнения его диагоналей.
. Найти координаты вершин квадрата и составить уравнения его диагоналей.
11. Составить уравнение плоскости, проходящей через точку A(1, 2, 0) параллельно векторам 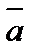 = (1, –1, 0) и
= (1, –1, 0) и 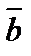 = (0, 4, –2).
= (0, 4, –2).
12. Составить канонические и параметрические уравнения прямой, заданной как пересечение двух плоскостей 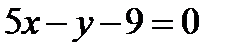 и
и 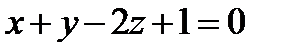 .
.
13. Найти основание перпендикуляра, опущенного из точки A(3, 0, -2) на плоскость p: 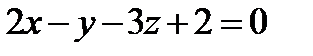 .
.
14. Вычислить определитель третьего порядка по правилу треугольников, разложив по первому столбцу:
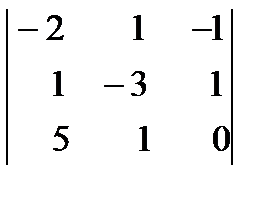 .
.
15. Решить систему уравнений тремя способами: а) методом Гаусса; б) по формулам Крамера; в) записать систему в ма-тричной форме и решить ее с помощью обратной матрицы.
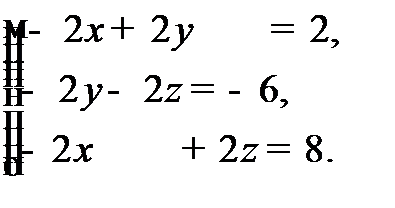
16. Исследовать систему уравнений на совместность и в случае совместности найти ее решение.
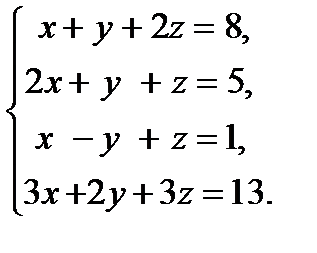
ВАРИАНТ 11
1. ABCDEF – правильный шестиугольник. Выразить через векторы 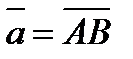 и
и 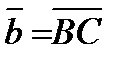 векторы
векторы 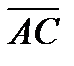 и
и 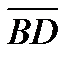 .
.
2. Разложить вектор 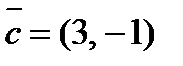 по векторам
по векторам 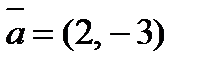 и
и 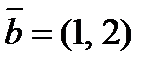 .
.
3. Вычислить 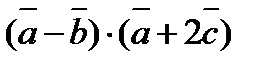 , если
, если 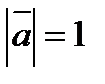 ,
, 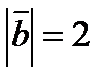 ,
, 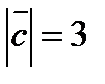 ,
, 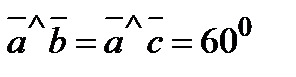 и
и 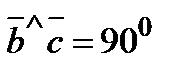 .
.
4. Вычислить проекцию вектора 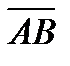 на ось вектора
на ось вектора 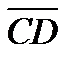 , если A(-2, 3, -4), B(3, 2, 5), С(1, -1, 2) и D(3, 2, -4).
, если A(-2, 3, -4), B(3, 2, 5), С(1, -1, 2) и D(3, 2, -4).
5. При каком значении a векторы 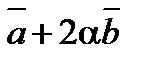 и
и 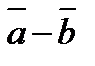 будут ортогональны, если
будут ортогональны, если 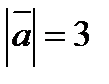 и
и 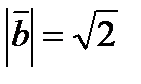 ,
, 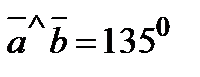 .
.
6. Найти 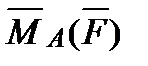 – момент силы
– момент силы 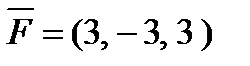 , приложенной в точке B(5, -3, 1), относительно точки A(4, -2, 3).
, приложенной в точке B(5, -3, 1), относительно точки A(4, -2, 3).
7. Является ли четырехугольник с вершинами в точках A(2, -1, 3), B(1, 2, -1), D(-4, 7, 5) и C(-5, 10, 1) параллелограммом? Если - да, то найти его площадь.
8. Лежат ли точки A(-1, -1, -1), B(-2, 1, -2), C(-1, 0, -2) и D(3, 2, 1) в одной плоскости?
9. Определить острый угол между высотой и медианой треугольника ABC, проведенными из вершины A, если координаты вершин известны: A(-2, 3), B(5, 7) и C(-3, -2).
10. Найти площадь ромба и координаты его вершин, если одна из его сторон и одна из диагоналей лежат соответственно на прямых L1: 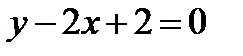 и L2:
и L2: 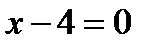 , а длина диагонали равна 12. Сколько решений имеет задача?
, а длина диагонали равна 12. Сколько решений имеет задача?
11. Составить уравнение плоскости , проходящей через точки A(1, 2, -1) и B(0, 3, 2) параллельно вектору 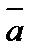 = (3, 4, 7).
= (3, 4, 7).
12. Составить параметрические и канонические уравнения прямой, заданной как пересечение двух плоскостей: 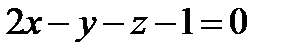 и
и 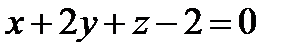 .
.
13. Найти проекцию точки A(1, 2, -3) на прямую, заданную как пересечение двух плоскостей: 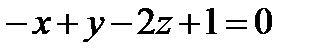 и
и 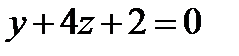 .
.
14. Вычислить определитель третьего порядка по правилу треугольников, разложив по второму столбцу:
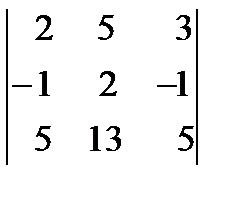 .
.
15. Решить систему уравнений тремя способами: а) методом Гаусса; б) по формулам Крамера; в) записать систему в ма-тричной форме и решить ее с помощью обратной матрицы.
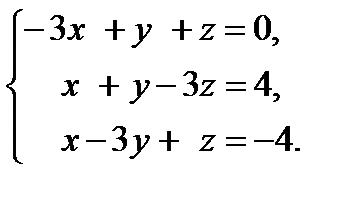
16. Исследовать систему уравнений на совместность и в случае совместности найти ее решение .
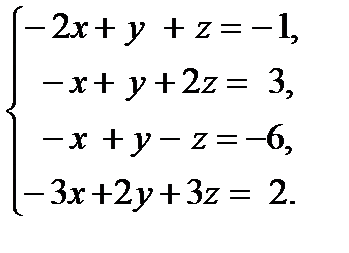
ВАРИАНТ 12
1. В треугольнике ABC точка М делит сторону AB на отрезки AM = 3 и MB = 1, а точка N делит сторону BC на отрезки BN = 3 и NC = 2. Выразить вектор 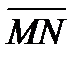 через векторы
через векторы 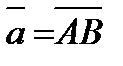 и
и 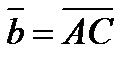 .
.
2. Разложить вектор 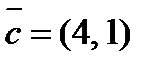 по векторам
по векторам 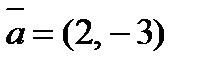 и
и 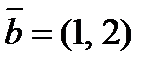 .
.
3. Вычислить 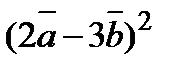 , если
, если 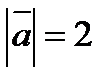 ,
, 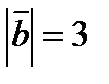 и
и  .
.
4. Вычислить проекцию вектора 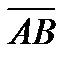 на ось вектора
на ось вектора 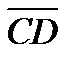 , если A(1, 1, 1), B(2, 3, 4), С(0, 1, 2) и D(2, 3, 1).
, если A(1, 1, 1), B(2, 3, 4), С(0, 1, 2) и D(2, 3, 1).
5. При каком значении a векторы 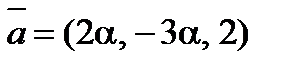 и
и 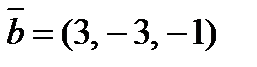 будут ортогональны?
будут ортогональны?
6. Найти 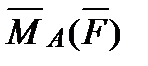 – момент силы
– момент силы 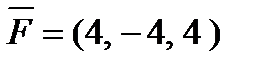 , приложенной в точке B(6, -4, 1), относительно точки A (5, -3, 3).
, приложенной в точке B(6, -4, 1), относительно точки A (5, -3, 3).
7. При каком значении a вектор 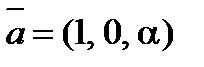 ортогонален вектору
ортогонален вектору 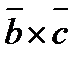 , если
, если 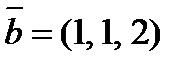 и
и  .
.
8. Лежат ли точки A(1, 1, 1), B(2, 0, 1), C(3, 1, -1) и D(4, -2, -2) в одной плоскости?
9. Определить острый угол между высотой и медианой треу-гольника ABC, проведенными из вершины A, если коорди-наты вершин известны: A(-1 ,1), B(6, 5) и C(-2, -4).
10. Найти площадь ромба и координаты его вершин, если одна из его сторон и одна из диагоналей лежат соответственно на прямых L1: 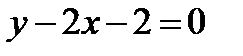 и L2:
и L2: 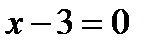 , а длина диагонали равна 12. Сколько решений имеет задача?
, а длина диагонали равна 12. Сколько решений имеет задача?
11. Составить уравнение плоскости, проходящей через точки A(-4, 3, 2) и B(2, 1, -1) параллельно прямой 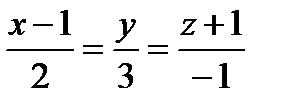 .
.
12. Составить параметрические и канонические уравнени
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|