Ключи.. Задача 1.. Задача 2.. Задача 3.. Задача 4.

Стр 1 из 2Следующая ⇒

Ключи.

Олимпиада по астрономии и физике космоса

(муниципальный тур)

11 Класс

Задача 1.

Суммарный блеск первой группы звезд ( от 3^m до 4^m ) составляет около

m_3-4=3.5 ^m – 2.5^m lg400 = -3.0^m

а второй группы (от 4^m до 5^m) около

m_4-5 = 4.5^m – 2.5 lg1100 = -3.1^m

Это означает, что обе группы практически равноценны по суммарному блеску. Любопытно, что такая закономерность сохраняется вплоть до очень больших m.

Система оценивания :

За каждый правильный ответ пункта задания выставляется 2 балла.

Записана правильно формула Погсона	2 балла
Верно посчитан суммарный блеск первой группы звезд	2 балла
Верно посчитан суммарный блеск второй группы звезд	2 балла
Верно сделан вывод по суммарному блеску	2 балла

Задача 2.

Будет, поскольку орбитальное движение Земли приводит к кажущемуся обращению Солнца вокруг нее с периодом в 1 год.

Дан только правильный ответ	4 балла
Правильный ответ сопровождается с пояснительными рисунками	8 баллов
Дан пояснительный рисунок верный, но нет ответа правильного	4 балла

Задача 3.

Луна движется навстречу суточному вращению небесной сферы со скоростью около 13˚ в сутки. Небесная сфера вращается со скоростью 15˚ в час. Значит восход Луны будет запаздывать каждый день на 60 ^m х (13˚/15˚) = 52^m. После восхода во вторник перед полуночью в среду Луна не взойдет, а появится только в четверг вскоре после полуночи в 0^h 37^m.

Написан только правильный ответ, без расчетов и пояснений	2 балла
Даны правильные пояснения, но числовой ответ не верен	5 баллов
Дан правильный ответ с объяснениями	8 баллов

Задача 4.

Рассмотрим задачу в общем случае. Пусть R_с и R_п – радиусы спутника и планеты, r_c и r_п – радиусы орбит спутника и планеты. Тогда наблюдаемый с поверхности планеты максимальный угловой диаметр спутника, выраженный в градусах (57,3˚ ≈ 1 рад) будет

α_с =114,6˚ * R_c / (r_c – R_п)

а угловой диаметр Солнца

α_ʘ = 0,5˚ / r _п (а.е.)

Условием полного солнечного затмения будет неравенство α_с ≥ α_ʘ .

r _п (а.е.) > (r_c – R_п) / 229,2 R_c .

Для Титана и Сатурна это условие выполняется с большим запасом. Для R_п = 60 тысяч км и r _п = 9,5 а.е. получим α_ʘ = 3,2 ' и α_с = 15,2'.

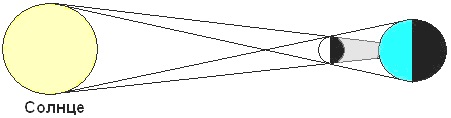
Возможно и другое решение этой задачи – поэтапное. За это снимать баллы нельзя.

Правильно рассчитан угловой диаметр спутника	2 балла
Правильно рассчитан угловой диаметр Солнца	2 балла
Указано условие возникновения солнечного затмения	2 балла
Есть пояснительный рисунок	2 балла

12 Следующая ⇒