Взаимное расположение прямой и плоскости

Выполните практическую работу

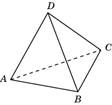
Взаимное расположение прямой и плоскости

1 часть

В тетраэдре 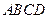точка 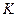- середина ребра 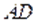, 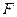- середина ребра 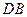, 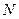- середина 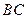, 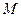- середина ребра .

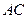Сделайте рисунок по условию задачи и заполните таблицу, выбрав в ней нужное обозначение расположения данных прямой и плоскости:

А – пересекаются; Б – параллельны; В – прямая лежит в плоскости; Г – невозможно определить.

	Прямая и плоскость	Взаимное расположение
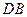	и
	и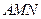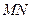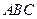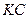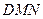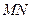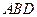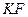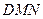
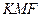	и
	и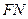
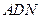	и
	и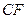
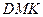	и
	и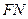

2 часть

Сделайте чертежи по заданным условиям:

1. Прямая 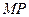параллельна плоскости 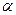, а прямая 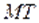пересекает эту плоскость в точке .

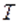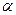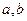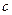2. Плоскость пересекает три параллельных прямых и соответственно в точках 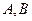и 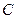, лежащих на одной прямой.

3. Плоскость 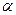пересекает три параллельных прямых 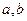и 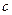соответственно в вершинах .

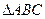4. Основание 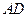трапеции 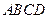лежит на плоскости 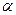, а прямые 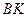и 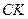пересекают эту плоскость соответственно в точках 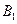и .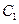

5. Плоскость 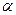проходит через середины сторон 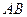и 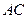треугольника 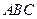и не содержит вершины .

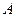Взаимное расположение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости

Все возможные случаи взаимного расположения прямой и плоскости в пространстве представлены в следующей таблице.

Фигура	Рисунок	Формулировка
Прямая лежит на плоскости (принадлежит плоскости)		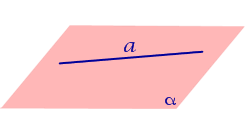Прямая лежит на плоскости, если все точки прямой принадлежат плоскости. Замечание. Для того, чтобы прямая лежала на плоскости, необходимо и достаточно, чтобы две любые точки этой прямой принадлежали этой плоскости.
Прямая пересекает плоскость		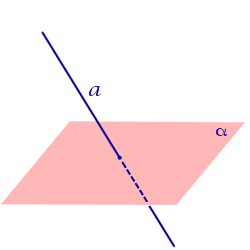Прямая пересекает плоскость, если прямая и плоскость имеют единственную общую точку.
Прямая параллельна плоскости		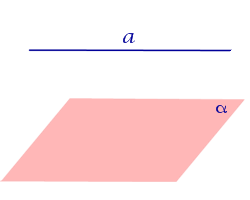Прямая параллельна плоскости, если прямая и плоскость не имеют общих точек. (они не пересекаются)

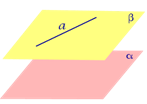
Утверждение 1. Предположим, что прямая a и плоскость α параллельны, а плоскость β проходит через прямую a .Тогда возможны два случая:

1. Плоскость β параллельна плоскости α (рис.1);

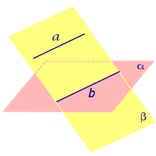
2. Плоскость β пересекает плоскость α. В этом случае прямая b , которая является линией пересечения плоскостей α и β , будет параллельна прямой a (рис.2).


Рис.1	Рис.2

Утверждение 2 (признак параллельности прямой и плоскости). Если прямая a , не лежащая в плоскости α , параллельна некоторой прямой b, лежащей в плоскости α , то прямая a и плоскость α параллельны.