
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практикум по аналитической геометрии (24.09.20 г.)
Практикум по аналитической геометрии (24.09.20 г.)
Задача 1.Даны две прямые, каждая из которых задана точкой и направляющим единичным вектором:
Пр 1: 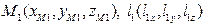 ;
;
Пр 2: 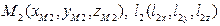 .
.
Определить их взаимное расположение и его характерные величины. Составить программу на Matlab, решающую эту задачу.
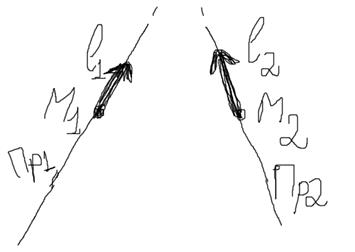
Рисунок 1 – Общее расположение двух прямых и их характерные величины
Решение.
Возможны четыре случая взаимного расположения двух прямых.
Случай 1. Прямые совпадают.
Случай 2. Прямые параллельны; характерной величиной является расстояние между ними;
Случай 3. Прямые пересекаются; характерным объектом является точка их пересечения;
Случай 4. Прямые скрещиваются; характерным объектами являются: точки на каждой из них, между которыми проходит кратчайший отрезок, и длина этого отрезка.
Прежде всего, зададим две прямые их каноническими уравнениями:
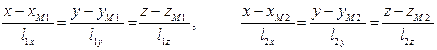 . (1)
. (1)
Рассмотрим случай 1. Прямые совпадают, если существует по крайней мере две различные точки, через которые проходят обе прямые. Очевидно, что достаточно проверить условия:
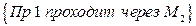 и
и 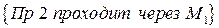 .
.
Это эквивалентно выполнению следующих уравнений:
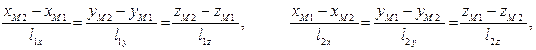 (2)
(2)
которые являются необходимыми и достаточными условиями совпадения двух прямых.
Рассмотрим случай 2. Прямые параллельны, если координаты их направляющих векторов пропорциональны друг другу, а точки 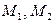 - различны, т.е.:
- различны, т.е.:
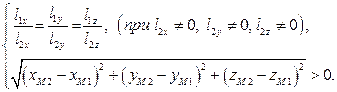 (3)
(3)
Эти условия являются необходимыми и достаточными для выполнения Случая 2.
Найдем расстояние между прямыми. Для этого возьмем, например, точку 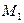 на первой прямой и найдем ближайшую к ней точку
на первой прямой и найдем ближайшую к ней точку 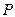 на второй прямой.
на второй прямой.

Рисунок 2 – Случай параллельных прямых
Вектор 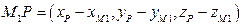 должен быть перпендикулярен обеим прямым, в частности, Пр. 1, поэтому скалярное произведение
должен быть перпендикулярен обеим прямым, в частности, Пр. 1, поэтому скалярное произведение 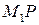 на
на 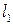 должно быть равно нулю:
должно быть равно нулю:
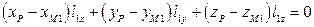 . (4)
. (4)
Второе уравнение получается, если учесть, что точка 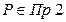 :
:
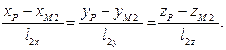 (5)
(5)
Три последних уравнения приводятся к виду:
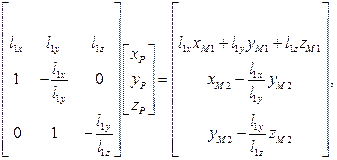 (6)
(6)
где учтены первые два уравнения в (3).
Найдя из (6) координаты точки 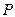 , далее находим кратчайшее расстояние между прямыми как модуль вектора
, далее находим кратчайшее расстояние между прямыми как модуль вектора 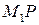 :
:
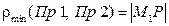 . (7)
. (7)
Рассмотрим случай 3. Для определения того, пересекаются ли данные прямые, перейдем от канонических их уравнений к соответствующим параметрическим:
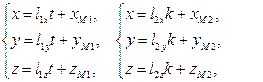 (8)
(8)
где 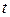 и
и 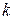 - параметры вдоль первой и второй прямых.
- параметры вдоль первой и второй прямых.
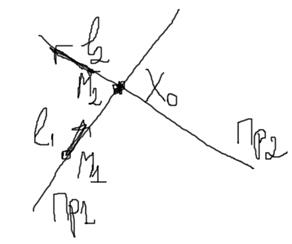
Рисунок 3 – Случай пересечения двух прямых
Пусть прямые пересекаются в некоторой точке 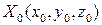 (см. рис. 3), тогда в этой точке параметр
(см. рис. 3), тогда в этой точке параметр 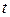 принимает некоторое значение
принимает некоторое значение 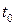 , а параметр
, а параметр 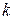 - значение
- значение 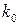 . И эти параметры должны удовлетворять шести уравнениям в (8).
. И эти параметры должны удовлетворять шести уравнениям в (8).
Возьмём первые два уравнения из каждой из подсистем в (8) и приравняем их правые части, поскольку левые одинаковы и равны 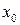 :
:
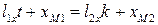 . (9)
. (9)
Аналогично поступаем со вторыми и третьими уравнениями этих двух подсистем:
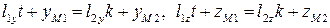 . (10)
. (10)
Три уравнения (9) и (10) образуют систему относительно неизвестных параметров 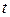 и
и 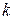 , но эта система переопределена. Возьмем такие два уравнения из этих трех, чтобы определитель полученной системы был ненулевой. Например, если для первых двух уравнений выполнено:
, но эта система переопределена. Возьмем такие два уравнения из этих трех, чтобы определитель полученной системы был ненулевой. Например, если для первых двух уравнений выполнено:
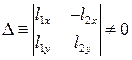 , (11)
, (11)
тогда из них можно найти неизвестные 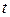 и
и 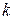 :
:
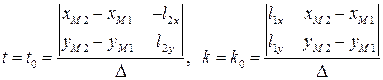 . (12)
. (12)
Далее необходимо проверить, удовлетворяет ли найденная пара  третьему уравнению, т.е. второму в (10):
третьему уравнению, т.е. второму в (10):
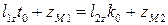 . (13)
. (13)
Если (13) выполняется, то прямые Пр 1 и Пр 2 пересекаются в точке 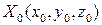 с координатами:
с координатами:
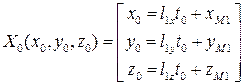 . (14)
. (14)
В противном случае – не пересекаются.
Заметим, что, если определитель 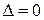 , то необходимо взять другой набор из двух уравнений для определения значений параметров
, то необходимо взять другой набор из двух уравнений для определения значений параметров  , например, первое и третье, или второй и третье уравнения, и если соответствующий определитель не нулевой, то проделать по аналогии все вышеперечисленные действия.
, например, первое и третье, или второй и третье уравнения, и если соответствующий определитель не нулевой, то проделать по аналогии все вышеперечисленные действия.
Рассмотрим случай 4. Если прямые не совпадают, не параллельны и не пересекаются, тогда они скрещиваются.
В этом случае существуют такие точки 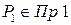 ,
, 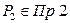 , что длина вектора
, что длина вектора 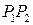 есть кратчайшее расстояние между этими прямыми. При этом направляющий вектор
есть кратчайшее расстояние между этими прямыми. При этом направляющий вектор 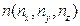 этого отрезка перпендикулярен направляющим векторам
этого отрезка перпендикулярен направляющим векторам 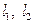 обеих прямых:
обеих прямых: 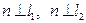 (см. рис. 4).
(см. рис. 4).
Вначале найдем 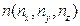 . В силу предыдущего, скалярные произведения вектора
. В силу предыдущего, скалярные произведения вектора 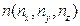 на
на 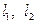 нулевые:
нулевые:
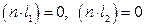 ,
,
поэтому:
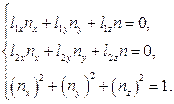 (15)
(15)
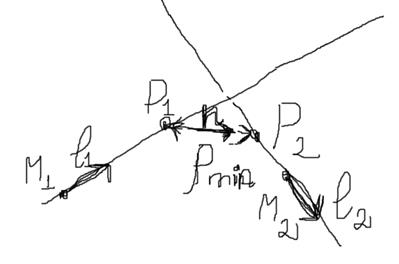
Рисунок 4 – Случай двух скрещивающихся прямых
Можно показать, что одно из двух решений (15) дается равенствами:
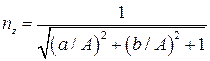 ,
, 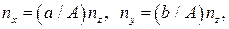
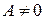 , (16)
, (16)
где
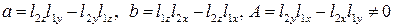 . (17)
. (17)
Заметим, что если 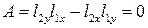 , то надо выразить
, то надо выразить  через
через 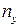 , либо
, либо 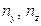 через
через 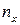 , чтобы соответствующий знаменатель в формулах, аналогичных (16), не был равен нулю.
, чтобы соответствующий знаменатель в формулах, аналогичных (16), не был равен нулю.
Далее, поскольку по условию 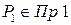 ,
, 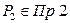 и вектор
и вектор 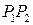 коллинеарен
коллинеарен 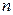 ,
,
то можно получить следующую систему уравнений относительно координат точек 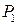 и
и 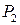 :
:
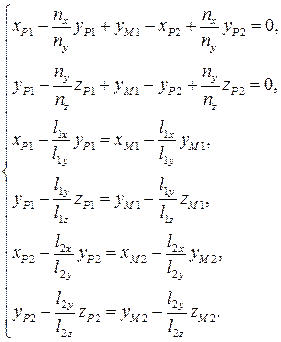 (18)
(18)
Если определитель этой системы отличен от нуля, тогда прямые скрещиваются. Тогда искомое кратчайшее расстояние между этими прямыми находится по формуле:
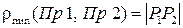 . (19)
. (19)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|