Неопределенности вида и с помощью тождественных преобразований сводятся к неопределенностям или и затем раскрываются по правилу Лопиталя.

Неопределенность возникает, если требуется найти при условии .

В результате преобразования (либо ) получается неопределенность (либо ).

Если нужно найти , причем и , то, представив разность , получим неопределенность .

Неопределенности вида путем логарифмирования выражения сводятся к неопределенности , рассмотренной выше.

Пример 4. Найти .

Решение. Здесь имеем неопределенность . Перепишем данное выражение в виде .

Теперь можно применить правило Лопиталя:

Пример 5. Найти .

Решение.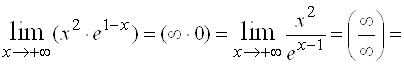

Пример 6. Найти .

Решение. Данное выражение представляет собой неопределенность вида 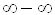. Преобразуем его к другому виду:

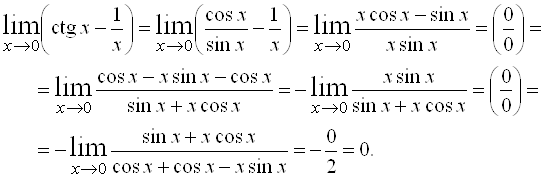
Пример 7. Найти .

Решение. .

Пример 8. Найти .

Решение. Здесь неопределенность вида . Обозначим и прологарифмируем: , откуда в силу непрерывности логарифмической функции (пример 4). Итак, , откуда , т. е. .

Пример 9. Найти .

Решение. Имеем неопределенность , которую можно было бы раскрыть с помощью второго замечательного предела, однако мы иллюстрируем другой прием. Обозначим , тогда

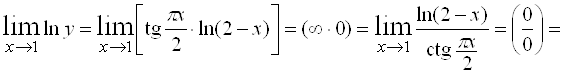
Получим , тогда по определению логарифма .

⇐ Предыдущая 12