Как пользоваться таблицами критических значений

Как пользоваться таблицами критических значений

Зачем нужны таблицы критических значений. Когда мы находим любое эмпирическое значение, рассчитанное по формуле (будь то проверка крайних значений в упорядоченном ряду на аномальность, или проверка соответствия эмпирического распределения нормальному, или расчет любого другого критерия для любых типов выборок), нам нужно понять, что данное число означает.

В случае расчета аномальных значений может быть 2 варианта: найденное по формуле эмпирическое значение (для min или max величин в упорядоченном ряду) может говорить о том, что наше число, в отношении которого производилась проверка, является аномальным (и тогда из дальнейших расчетов мы его исключаем) или наоборот, не является аномальным. Чтобы решить эту проблему, нам нужен некий ориентир, или число, относительно которого мы сможем сказать, что если наше эмпирическое значение критерия оказалось больше этого ориентира – критического значения, то наше число является аномальным, а если меньше – то аномальным не является.

Для любого статистического критерия существуют свои таблицы критических значений. Выбор нужного критического значения осуществляется либо по объему выборки (n), либо по числу степеней свободы (рассчитывается для каждого критерия по-своему, но зависит всегда от объема выборки). Для аномальных значений расчет ведется по объему выборки. В большинстве случаев критические значения рассчитаны для двух или трех уровней значимости (р):

- критическое значение для уровня значимости р = 0,05 означает, что если наше эмпирическое значение критерия равно этому табличному критическому значению, то принимая гипотезу о том, что наше число является аномальным, мы можем дать 95% гарантии того, что наше утверждение верно, и сохраняется 5% вероятности ошибки. Все эмпирические значения, оказавшиеся меньше этого критического значения, мы не будем считать аномальными. Для всех эмпирических значений, которые больше критического значения для р = 0,05, но меньше критического значения для p=0,01, мы будем считать, что они являются аномальными, но с вероятностью ошибки в 5% или меньше (p < 0,05)

- если наше эмпирическое значение оказалось больше критического для р=0,01, то мы также говорим о том, что число, в отношении которого производился расчет критерия, является аномальным, но вероятность ошибки при этом равна 1% или менее (р < 0,01).

- если есть в таблице критическое значение, рассчитанное для р=0,001, то мы его также принимаем во внимание, т к если наше эмпирическое число окажется больше и этого критического, то мы сможем дать гарантию 99,9% того, что наши расчеты верны, а вероятность ошибки при этом будет менее 0,1% (р<0,001), то есть это повышает надежность наших расчетов.

Теперь разберем то же самое, но уже на примере таблицы критических аномальных значений:

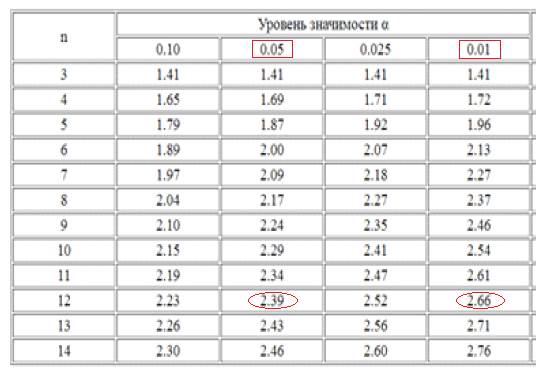
Для выборки объемом 12 человек (измеренных значений) находим критические значения (акр) для р = 0,05 и р = 0,01. Если наше эмпирическое число amax или amin меньше, чем 2,39, то соответствующие им максимальное или минимальное значения аномальными не являются:

если Аmin (Amax) < Акр (р=0,05), то значение хmin (xmax) не является аномальным.

Если рассчитанное эмпирическое значение находится между двумя критическими (в данном случае больше 2,39 и меньше 2,66), то соответствующее ему число является аномальным с вероятностью ошибки в 5% или менее:

если Акр (р=0,05)< Аmin (Amax) <Акр(p=0,01), то значение хmin (xmax) является аномальным (р<0,05)

Ну и в случае, если найденное эмпирическое значение больше критического значения для р=0,01 (то есть в данном примере больше 2,66), то оно является аномальным с вероятностью ошибки в 1% или менее:

Если Аmin (Amax) > Акр(p=0,01), то значение хmin (xmax) является аномальным (р<0,01).

В случае расчета критерия x2 Пирсона, нужно помнить, что критические значения выбираются не по объему выборки, по числу степеней свободы, рассчитанному исходя из количества интервалов, которые вы произвольно выбрали для вычисления критерия. Число степеней свободы будет равно количеству интервалов минус 3. Например, если у вас было 7 интервалов, то критические значения нужно искать для числа степеней свободы 4.

И второе отличие критерия – это допустимая величина ошибки, которая может равняться 20% (то есть в таблице ищем значение для р=0,2):

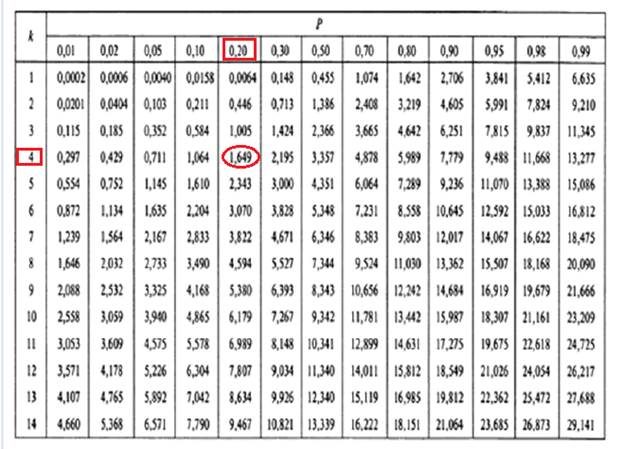
Чем больше величина эмпирического значения критерия х2эмп, тем больше наше эмпирическое распределение отличается от нормального. То есть, в нашем примере, если х2эмп меньше числа 1,649, то наше эмпирическое распределение значимо не отличается от нормального:

если

Если если х2эмп больше числа 1,649, то наше эмпирическое распределение значимо отличается от нормального, и вероятность ошибки при этом будет меньше или равна 20%:

Если х2эмп > x2кр (р=0,2), то тип распределения значимо отличается от нормального (p<0,2)

Почему допускается ошибка в 20%? В случае проверки типа распределения результатом является выбор критерия. Если распределение нормальное – пользуемся параметрическими критериями, если ненормальное – то непараметрическими. И если распределение нормальное, а мы применим непараметрический критерий, то расчеты все равно окажутся верными, просто для нас они могут быть сложнее по процедуре, чем если бы мы применили параметрический критерий. А вот если мы выборку с ненормальным распределением будим пытаться «просчитывать» параметрическими критериями, то существующие закономерности можем просто не обнаружить, потому как параметрические критерии очень чувствительны к параметрам выборки – среднему, дисперсии, стандартному отклонению. Таким образом, лучше выборку с нормальным распределением ошибочно определить, как «ненормальную», чем наоборот.

Ну и отдельно нужно сказать о таблице накопленного нормального распределения. Данная таблица составлена только для положительных значений z. Но как вы помните, ось Y делит график z-распределения ровно пополам, и z=0 это и среднее арифметическое, и мода, и медиана. Но поскольку график абсолютно симметричный, то найденные значения z для наших интервалов мы можем просто зеркально отразить со знаком минус. При этом 50% всей площади под графиком будет лежать слева от оси Y(и там будут отрицательные значения z), а вторые 50% - справа (положительные значения z).

Допустим, мы хотим сделать расчет критерия х2 Пирсона с количеством интервалов, равным 9. Вся площадь под кривой Z равна 1 (это мы знаем из свойств z-распределения). Если мы эту площадь поделим на 9 одинаковых частей, то каждый из 9 кусочков этой площади будет равен:

1:9=0,1111

Распишем, как будет накапливаться площадь от интервала к интервалу (двигаемся слева направо по оси z):

1 интервал – 0,1111

2 интервал – 0,2222

3 интервал – 0,3333

4 интервал – 0,4444

5 интервал – 0,5555

6 интервал – 0,6666

7 интервал – 0,7777

8 интервал – 0,8888

9 интервал – 0,9999

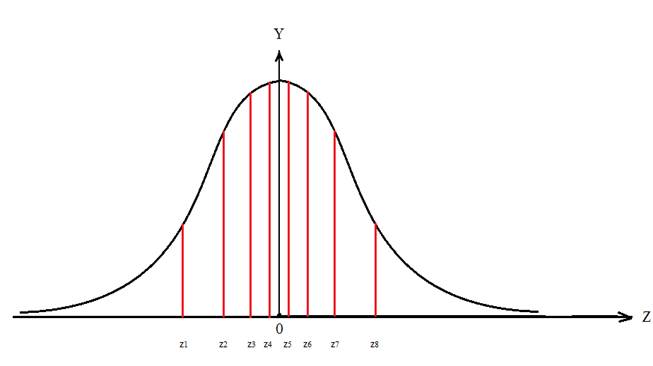
В таблице площадей мы можем найти соответствующие точки z, разделяющие наши 9 кусочков площади. Но поскольку в таблице только положительные значения z, то мы можем там найти точки z5(конец 5ого интервала), z6(конец 6ого интервала), z7 (конец 7ого интервала), и z8 (конец 8ого интервала), (см. рис.) Значение z для 9ого интервала нам искать не надо, т. к. в 9й интервал попадут все значения больше z8. В таблице площадей ищем нужные значения площадей (самые близкие значения) и выписываем соответствующие им значения z:

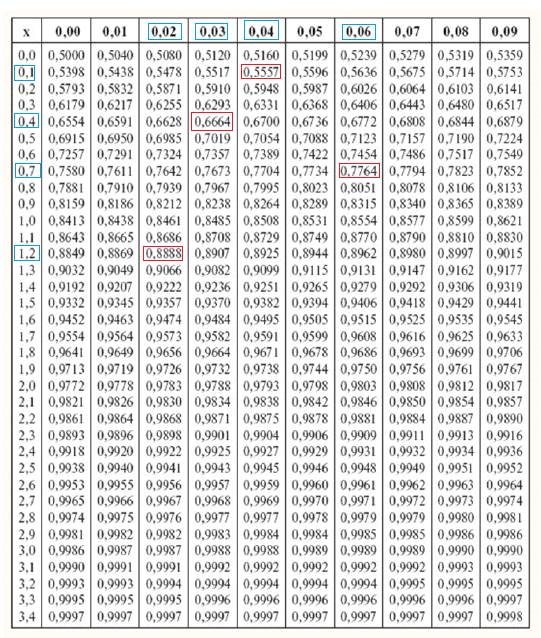
Точке z5 соответствует площадь, равная 0,5555. Ищем это значение в поле таблицы, и смотрим, на пересечении каких строк и столбиков оно находится. Слева по вертикали даны значения величин с десятыми числами после запятой, сверху – сотые после запятой. То есть Z5 будет равна 0,14. Таким же образом ищем остальные точки Z:

- Z6 = 0,43 (накопленная площадь 0,6666)

- Z7 = 0,76 (накопленная площадь 0,7777)

- Z8 = 1,22 (накопленная площадь 0,8888)

Теперь мы зеркально отображаем эти значения на первую половину графика с отрицательными значениями (см. график выше) и получаем точки:

-Z1 = -1,22 (накопленная площадь 0,1111)

-Z2 = -0,76 (накопленная площадь 0,2222)

-Z3 = -0,43 (накопленная площадь 0,3333)

-Z4 = - 0,14 (накопленная площадь 0,4444)

Как мы помним – площадь, по сути, это количество всех результатов, оказавшихся в заданном интервале. Все возможные нормальные распределения отличаются друг от друга только средним арифметическим и стандартным отклонением. То есть, исключив эти 2 параметра, мы получим z-распределение.

А теперь вернемся к нашей выборке. Нам известен объем выборки (допустим, для примера, n=90). Tогда, если у нас в выборке нормальное распределение и мы поделим весь объем выборки на 9 равных частей, то у нас в каждой части должно оказаться по 10 результатов (теоретическая частота). Теперь нам осталось выяснить, сколько же на самом деле результатов окажется в каждом из 9 интервалов. Для этого нам нужно упорядочить все значения по возрастанию и перевести их в z-баллы, а потом посчитать, сколько результатов у нас попало в каждый интервал:

- от -∞ до точки z1= -1,22 (1й интервал, эмпирическая частота f1)

- от z1= -1,22 до z2= -0,76 (2й интервал, эмпирическая частота f2)

- от z2= -0,76 до z3 = -0,43 (3й интервал, эмпирическая частота f3)

И так далее рассчитываем эмпирическую частоту для каждого из 9 интервалов. Далее все подставляем в расчетную формулу x2 Пирсона и получаем эмпирическое значение критерия, которое далее сравниваем с критическим табличным значением.