
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Направление выпуклости графика функции. Точка перегиба
Направление выпуклости графика функции. Точка перегиба
График функции называется выпуклым в некотором интервале, если в этом интервале он расположен ниже любой своей касательной.
График функции называется вогнутым в некотором интервале, если в этом интервале он расположен выше любой своей касательной.
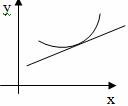
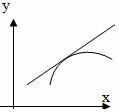
Достаточный признак выпуклости и вогнутости графика функции. Если вторая производная дважды дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка , то функция вогнута (выпукла) на этом промежутке.
Точкой перегиба графика непрерывной функции называется точка, в которой изменяется направление выпуклости и вогнутости.
Достаточный признак существования точки перегиба. Если в точке функция имеет первую производную, а вторая производная равна нулю или не существует и кроме того при переходе через меняет свой знак, то – точка перегиба.
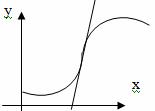
Правило нахождения точек перегиба
1) Найти область определения функции f(x).
2) Найти , решить уравнение и найти точки x из области определения, в которых или не существует.
3) Разбить область определения найденными в предыдущем пункте точками на промежутки, в которых вторая производная имеет один и тот же знак и в них найти знаки второй производной.
4) В промежутках, где вторая производная положительна, функция вогнутая, а в промежутках, где вторая производная отрицательна, функция выпуклая.
5) Найти точки перегиба.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|