
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Действительные числа. Целые и рациональные числа.
Тема: Действительные числа. Целые и рациональные числа.
Дата: 28.10.2020 г.
Группа: МОЦИ-264
Студенты должны знать: понятие множества целых, рациональных и действительных чисел
Студенты должны уметь: проводить сравнительный анализ полученного результата, пользоваться умением самопроверки, реализовывать всевозможные способы работы с разнообразием чисел.
 1.Актуализация опорных знаний
1.Актуализация опорных знаний

 2.Устный опрос:
2.Устный опрос:
3.Изучение новой темы.
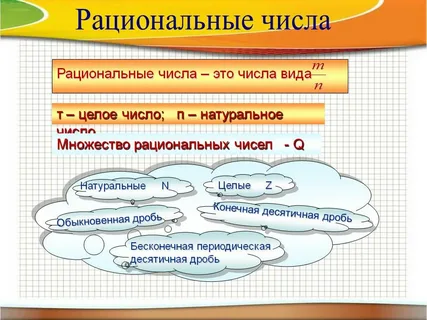
Итак, числа вида, где m – целое число, n – натуральное число, составляют множество рациональных чисел. Это множество принято обозначать заглавной латинской буквой. Кстати, любое целое число можно представить в виде рационального, например, число m можно представить в виде.
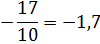
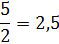 Множество рациональных чисел позволило находить частное любых двух целых чисел при условии, что делитель не равен нулю.
Множество рациональных чисел позволило находить частное любых двух целых чисел при условии, что делитель не равен нулю.
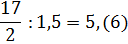
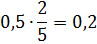
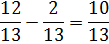
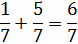 Кроме того, при выполнении всех четырёх арифметических действий (кроме деления на нуль) над рациональными числами всегда получают рациональные числа.
Кроме того, при выполнении всех четырёх арифметических действий (кроме деления на нуль) над рациональными числами всегда получают рациональные числа.
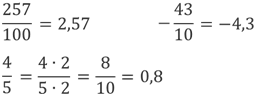 Рациональное число можно представить в виде дроби, где m – целое число, k– натуральное число. Если рациональное число можно представить в виде дроби, где m – целое число, k – натуральное число, то его можно записать в виде конечной десятичной дроби.
Рациональное число можно представить в виде дроби, где m – целое число, k– натуральное число. Если рациональное число можно представить в виде дроби, где m – целое число, k – натуральное число, то его можно записать в виде конечной десятичной дроби.
Заметим, что одно и то же рациональное число можно представить различными дробями, которые получаются из несократимой дроби умножением её числителя и знаменателя на одно и то же целое число, отличное от нуля.
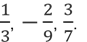 Существуют и рациональные числа, которые нельзя записать в виде конечной десятичной дроби.
Существуют и рациональные числа, которые нельзя записать в виде конечной десятичной дроби.
Если, например, мы попытаемся записать число в виде десятичной дроби, используя алгоритм деления уголком, то получим бесконечную десятичную дробь

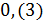
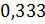 Напомним, что такую бесконечную десятичную дробь называют периодической, а повторяющуюся цифру 3 – её периодом. Нашу периодическую дробь … коротко записывают так: . А читают нашу периодическую дробь так: «нуль целых и три в периоде».
Напомним, что такую бесконечную десятичную дробь называют периодической, а повторяющуюся цифру 3 – её периодом. Нашу периодическую дробь … коротко записывают так: . А читают нашу периодическую дробь так: «нуль целых и три в периоде».
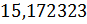 Тогда можем сделать такой вывод: любая периодическая дробь – это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или группа цифр – период дроби.
Тогда можем сделать такой вывод: любая периодическая дробь – это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или группа цифр – период дроби.
Например, десятичная дробь …. Она равна . 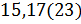 Это периодическая дробь с периодом 23. Читают эту дробь так: «пятнадцать целых семнадцать сотых и двадцать три в периоде».
Это периодическая дробь с периодом 23. Читают эту дробь так: «пятнадцать целых семнадцать сотых и двадцать три в периоде».
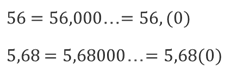 Заметим, что каждое целое число или конечную десятичную дробь можно считать и бесконечной десятичной периодической дробью с периодом, равным нулю.
Заметим, что каждое целое число или конечную десятичную дробь можно считать и бесконечной десятичной периодической дробью с периодом, равным нулю.
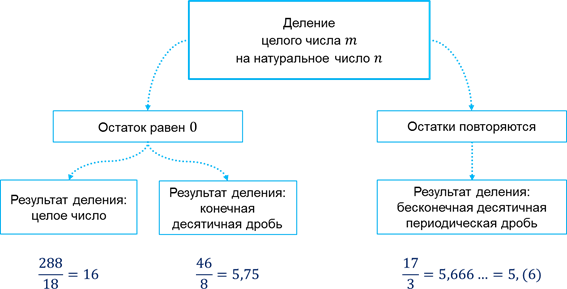 Вообще, при делении целого числа m на натуральное число n на некотором шаге остаток может стать равным нулю, тогда в результате деления получается целое число или конечная десятичная дробь. Либо же при делении целого числа m на натуральное число n на некотором шаге остатки начинают повторяться, так как каждый из остатков меньше n, тогда в результате деления получается бесконечная десятичная периодическая дробь.
Вообще, при делении целого числа m на натуральное число n на некотором шаге остаток может стать равным нулю, тогда в результате деления получается целое число или конечная десятичная дробь. Либо же при делении целого числа m на натуральное число n на некотором шаге остатки начинают повторяться, так как каждый из остатков меньше n, тогда в результате деления получается бесконечная десятичная периодическая дробь.
А теперь давайте приступим к практической части нашего урока.
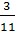
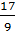 Итак, задание первое. Запишите в виде бесконечной десятичной дроби:
Итак, задание первое. Запишите в виде бесконечной десятичной дроби:
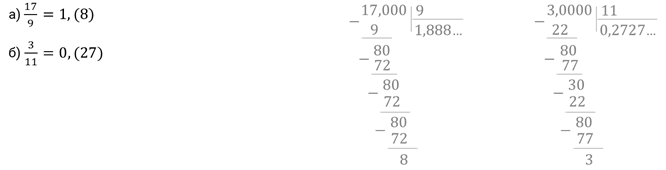 а) ; б) .
а) ; б) .
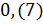
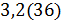 Задание второе. Запишите в виде обыкновенной дроби: а) ; б)
Задание второе. Запишите в виде обыкновенной дроби: а) ; б)
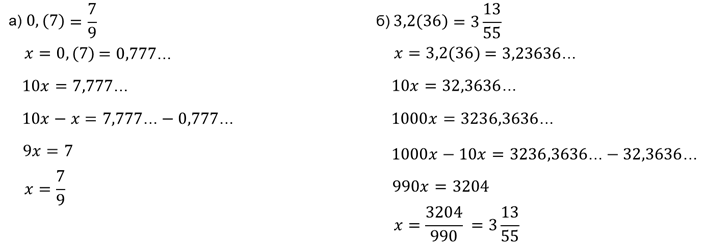
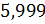
 И последнее задание. Покажите, что … .
И последнее задание. Покажите, что … .
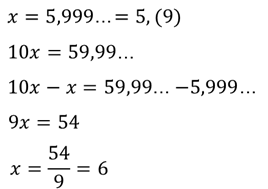
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|